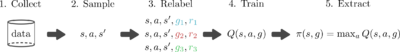Visual Reinforcement Learning with Imagined Goals: Difference between revisions
| Line 40: | Line 40: | ||
=Variational Autoencoder (VAE)= | =Variational Autoencoder (VAE)= | ||
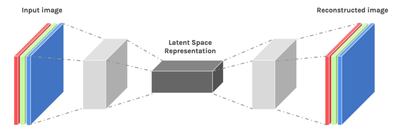
An autoencoder is a type of machine learning model that can learn to extract a robust, space-efficient feature vector from an image. The model has two parts — an encoder (e) and a decoder (p). The encoder takes as an input the image, and outputs a low-dimensional feature vector. The decoder takes as an input this low-dimensional feature vector, and recreates the original shape. | An autoencoder is a type of machine learning model that can learn to extract a robust, space-efficient feature vector from an image. The model has two parts — an encoder (e) and a decoder (p). The encoder takes as an input the image, and outputs a low-dimensional feature vector. The decoder takes as an input this low-dimensional feature vector, and recreates the original shape. | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">[[File:1 1OabPemOWCLrpCwIUmIsCg.png|400px]]</div> | |||
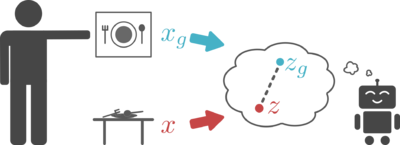
This generative model converts high-dimensional observations x, like images, into low-dimensional latent variables z, and vice versa. The model is trained so that the latent variables capture the underlying factors of variation in an image, similar to the abstract representations a human may use to interpret the world and goals. Given a current image x and goal image xg, we convert them into latent variables z and zg respectively. We then use these latent variables to representation the state and goal for our reinforcement learning algorithm. Learning Q functions and policies on top of this low-dimensional latent space rather than directly on images results in faster learning. | This generative model converts high-dimensional observations x, like images, into low-dimensional latent variables z, and vice versa. The model is trained so that the latent variables capture the underlying factors of variation in an image, similar to the abstract representations a human may use to interpret the world and goals. Given a current image x and goal image xg, we convert them into latent variables z and zg respectively. We then use these latent variables to representation the state and goal for our reinforcement learning algorithm. Learning Q functions and policies on top of this low-dimensional latent space rather than directly on images results in faster learning. | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">[[File:robot-interpreting-scene.png|400px]]</div> | |||
Using the latent variable representations for the images and goals also solves another problem: how to compute rewards. Rather than using pixel-wise error as our reward, we use the distance in the latent space for the reward to train our agent to reach a goal. In the full research paper describing our method, we show that this corresponds to maximizing the probability of reaching the goal and provides a much more effective learning signal. | Using the latent variable representations for the images and goals also solves another problem: how to compute rewards. Rather than using pixel-wise error as our reward, we use the distance in the latent space for the reward to train our agent to reach a goal. In the full research paper describing our method, we show that this corresponds to maximizing the probability of reaching the goal and provides a much more effective learning signal. | ||
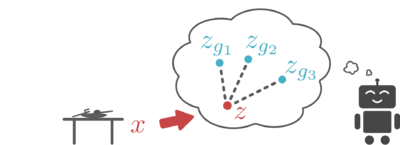
This generative model is also important because it allows an agent to easily generate goals in the latent space. In particular, our generative model is designed so that sampling latent variables is trivial: we just sample latents from the VAE prior. We use this sampling mechanism for two reasons: First, it provides a mechanism for an agent set its own goals. The agent simply samples a value for the latent variable from our generative model, and tries to reach that latent goal. Second, this resampling mechanism is also used to relabel goals as mentioned above. Because our generative model is trained to encode real images into the prior, the samples from our latent variable prior correspond to meaningful latent goals. | This generative model is also important because it allows an agent to easily generate goals in the latent space. In particular, our generative model is designed so that sampling latent variables is trivial: we just sample latents from the VAE prior. We use this sampling mechanism for two reasons: First, it provides a mechanism for an agent set its own goals. The agent simply samples a value for the latent variable from our generative model, and tries to reach that latent goal. Second, this resampling mechanism is also used to relabel goals as mentioned above. Because our generative model is trained to encode real images into the prior, the samples from our latent variable prior correspond to meaningful latent goals. | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">[[File:robot-imagining-goals.png|400px]]</div> | |||
All together, the latent variable representation of images (1) captures the underlying factors of a scene, (2) provides meaningful distances to optimize, and (3) provides an efficient goal sampling mechanism, allowing us to efficiently train a goal-conditioned reinforcement learning agent that operates directly on pixels. We call the overall method reinforcement learning with imagined goals (RIG). | All together, the latent variable representation of images (1) captures the underlying factors of a scene, (2) provides meaningful distances to optimize, and (3) provides an efficient goal sampling mechanism, allowing us to efficiently train a goal-conditioned reinforcement learning agent that operates directly on pixels. We call the overall method reinforcement learning with imagined goals (RIG). | ||
Revision as of 17:30, 14 November 2018
[Need add more pics and references]
Introduction and Motivation
Humans are able to accomplish many tasks without any explicit or supervised training, simply by exploring their environment. If I were dropped in the middle of Moscow, simply by walking around in an undirected manner, I could accomplish a specific task (ex. go to the grocery store) without ever having seen this task before simply by knowing where the store was located from past experience. We are able to set our own goals and learn from our experiences, and thus able to accomplish specific tasks without ever having been trained explicitly for them, a core principle of generalization.
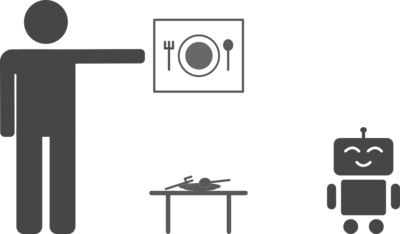
Naturally, the next question for any machine learning scientist is: can an autonomous agent also set its own goals and learn from its environment. In the paper “Visual Reinforcement Learning with Imagined Goals”, the authors are able to devise such an unsupervised reinforcement learning system. Specifically, they introduce a system that sets abstract goals and autonomously learns to achieve those goals. They then show that they can use these autonomously learned skills to perform a variety of user-specified goals, such as pushing objects, grasping objects, and opening doors, without any additional learning. Lastly, they demonstrate that their method is efficient enough to work in the real world on a Sawyer robot. The robot learns to set and achieve goals involving pushing an object to a specific location, with only images as the input to the system.
Related Work
Goal-Conditioned Reinforcement Learning
The ultimate directive in reinforcement learning is to learn a policy, that when given a state and goal, can dictate the optimal action. In this paper, goals are not explicitly defined during training. If a goal is not explicity defined, a set of synthetic goals must be autogenerated by the agent. Thus, suppose we let an autonomous agent explore an environment with a random policy. After executing each action, state observations are collected and stored. These state observations are structured in the form of images. The agent can randomly select goals from the set of state observations, and can also randomly select initial states from the set of state observations.
Now given a set of all possible states, a goal, and an initial state, a reinforcement learning framework can be used to find the optimal policy such that the value function is maximized. However, to implement such a framework, we need to define a reward function. One choice for the reward is the negative distance between the current state and the goal state, so that maximizing the reward corresponds to minimizing the distance to a goal state.
We can train a single policy to maximize rewards and therefore reach goal states by first learning a goal-conditioned Q function. A goal-conditioned Q function Q(s,a,g) tells us how good an action a is, given the current state s and goal g. For example, a Q function tells us, “How good is it to move my hand up (action a), if I’m holding a plate (state s) and want to put the plate on the table (goal g)?” Once this Q function is trained, you can extract a goal-conditioned policy by performing the following optimization
which effectively says, “choose the best action according to this Q function.” By using this procedure, we obtain a policy that maximizes the sum of rewards, i.e. reaches various goals.
One reason that Q learning is popular is that in can be done in an off-policy manner, meaning that the only things we need to train our Q function are samples of state, action, next state, goal, and reward: (s,a,s′,g,r). This data can be collected by any policy and can be reused across multiples tasks. So a simple goal-conditioned Q-learning algorithm looks like this:
The main bottleneck in this training procedure is collecting data. If we could artificially generate more data, we could in theory learn to solve various tasks without even interacting with the world. Unfortunately, learning an accurate model of the world is difficult, so we usually have to rely on sampling to get state-action-next-state data, (s,a,s′). However, if we have access to the reward function r(s,g), we can retroactively relabeled goals and recompute rewards, allowing us to artificially generate more data given a single (s,a,s′) tuple. So, we can modify this training procedure like so:
The nice thing about this goal resampling is that we can simultaneously learn how to reach multiple goals at once without needing more data from the environment. Overall, this simple modification can result in substantially faster learning.
The method outlined above makes two major assumptions: (1) you have access to a reward function and (2) you have access to a goal sampling distribution p(g). Prior works that use this goal relabeling strategy ( Kaelbling ‘93 , Andrychowicz ‘17 , Pong ‘18 ) operate on ground truth state information (e.g., the Cartesian position of an object), where it is easy to manually design both the goal distribution p(g) and reward function. However, when moving to vision-based tasks where goals are images, both of these assumptions introduce practical concerns.
For one, a fundamental problem with this reward function is that it assumes that the distance between raw images will yield semantically useful information. Images are noisy. A large amount of information in an image that may not be related to the object we analyze. Thus, the distance between two images may not correlate with their semantic distance.
Second, because our goals are images, we need a goal image distribution p(g) from which we can sample goal images. Manually designing a distribution over goal images is a non-trivial task and image generation is still an active field of research. Instead, we would like our agent to autonomously imagine its own goals and learn how to reach them.
Variational Autoencoder (VAE)
An autoencoder is a type of machine learning model that can learn to extract a robust, space-efficient feature vector from an image. The model has two parts — an encoder (e) and a decoder (p). The encoder takes as an input the image, and outputs a low-dimensional feature vector. The decoder takes as an input this low-dimensional feature vector, and recreates the original shape.
This generative model converts high-dimensional observations x, like images, into low-dimensional latent variables z, and vice versa. The model is trained so that the latent variables capture the underlying factors of variation in an image, similar to the abstract representations a human may use to interpret the world and goals. Given a current image x and goal image xg, we convert them into latent variables z and zg respectively. We then use these latent variables to representation the state and goal for our reinforcement learning algorithm. Learning Q functions and policies on top of this low-dimensional latent space rather than directly on images results in faster learning.
Using the latent variable representations for the images and goals also solves another problem: how to compute rewards. Rather than using pixel-wise error as our reward, we use the distance in the latent space for the reward to train our agent to reach a goal. In the full research paper describing our method, we show that this corresponds to maximizing the probability of reaching the goal and provides a much more effective learning signal.
This generative model is also important because it allows an agent to easily generate goals in the latent space. In particular, our generative model is designed so that sampling latent variables is trivial: we just sample latents from the VAE prior. We use this sampling mechanism for two reasons: First, it provides a mechanism for an agent set its own goals. The agent simply samples a value for the latent variable from our generative model, and tries to reach that latent goal. Second, this resampling mechanism is also used to relabel goals as mentioned above. Because our generative model is trained to encode real images into the prior, the samples from our latent variable prior correspond to meaningful latent goals.
All together, the latent variable representation of images (1) captures the underlying factors of a scene, (2) provides meaningful distances to optimize, and (3) provides an efficient goal sampling mechanism, allowing us to efficiently train a goal-conditioned reinforcement learning agent that operates directly on pixels. We call the overall method reinforcement learning with imagined goals (RIG).
Search Strategy
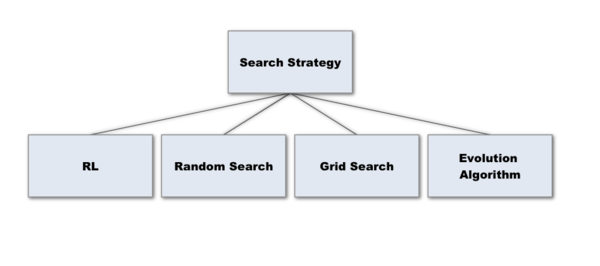
There are some common search strategies used in the field of NAS, such as Reinforcement learning, Random search, Evolution algorithm, and Grid Search.
The one they used in the paper is Random Search. It basically samples points from the search space uniformly at random as well as sampling some points that are close to the current observed best point. Intuitively it makes sense because it combines exploration and exploitation. When you sample points close to the current optimal point, you are doing exploitation. And when you sample points randomly, you are doing exploration.
They quoted from another paper that claims random search performs the random search is competitive with reinforcement learning and other learning techniques. [7]
In the implementation, they used Google's black box optimization tool Google vizier. It is not open source, but there is an open source implementation of it [8]
Performance Evaluation Strategy
The evaluation in this particular task is very tricky. The reason is we are evaluating neural network here. In order to evaluate it, we need to train it first. And we are doing pixel level classification on images with high resolutions, so the naive approach would require a tremendous amount of computational resources.
The way they solve it in the paper is defining a proxy task. The proxy task is a task that requires sufficient less computational resources, while can still give a good estimate of the performance of the network. In most image classical tasks of NAS, the proxy task is to train the network on images of lower resolution. The assumption is, if the network performs well on images with lower density, it should reasonably perform well on images with higher resolution.
However, the above approach does not work on this case. The reason is that the dense prediction tasks innately require high-resolution images as training data. The approach used in the paper is the flowing:
- Use a smaller backbone for proxy task
- caching the feature maps produced by the network backbone on the training set and directly building a single DPC on top of it
- Early stopping train for 30k iterations with a batch size of 8
If training on the large-scale backbone without fixing the weights of the backbone, they would need one week to train a network on a P100 GPU, but now they cut down the proxy task to be run 90 min. Then they rank the selected architectures, choosing the top 50 and do a full evaluation on it.
The evaluation metric they used is called mIOU, which is pixel level intersection over union. Which just the area of the intersection of the ground truth and the prediction over the area of the union of the ground truth and the prediction.
Result
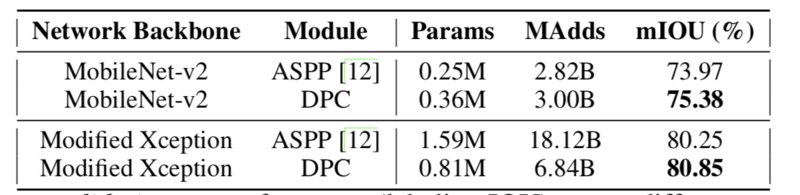
This method achieves state of art performances in many datasets. The following table quantifies the gain on performance on many datasets.
The chose to train on modified Xception network as a backbone, and the following are the resulting architecture for the DPC.
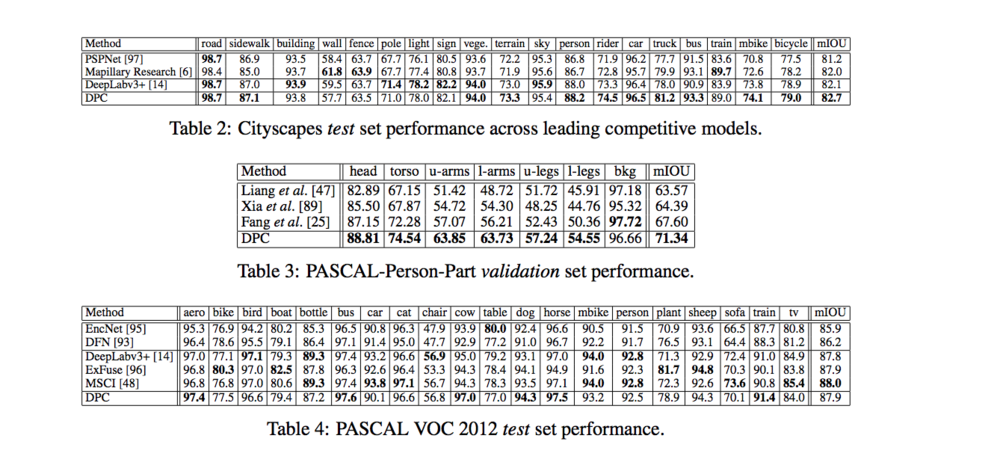
Table 2 describes the results on scene parsing dataset. It sets a new state-of-the-art performance of 82.7% mIOU and outperforms other state-of-the-art models across 11 of the 19 categories.
Table 3 describes the results on person part segmentation dataset. It achieve the state-of-the-art performance of 71.34% mIOU and outperforms other state-of-the-art models across 6 of the 7 categories.
Table 4 describes the results on semantic image segmentation dataset. It achieve the state-of-the-art performance of 87.9% mIOU and outperforms other state-of-the-art models across 6 of the 20 categories.
As we can see, the searched DPC model achieves better performance (measured by mIOU) with less than half of the computational resources(parameters), and 37% less of operations (add and multiply).
Future work
The author suggests that when increasing the number of branches in the DPC, there might be a further gain on the performance on the image segmentation task. However, although the random search in an exponentially growing space may become more challenging. There may need more intelligent search strategy.
The author hope that this architecture search techniques can be ported into other domains such as depth prediction and object detection to achieve similar gains over human-invented designs.
Critique
1. Rich man's game
The technique described in the paper can only be applied by parties with abundant computational resources, like Google, Facebook, Microsoft, and e.t.c. For small research groups and companies, this method is not that useful due to the lack of computational power. Future improvement will be needed on the design an even more efficient proxy task that can tell whether a network will perform well that requires fewer computations.
2. Benefit/Cost ratio
The technique here does outperform human designed network in many cases, but the gain is not huge. In Cityscapes dataset, the performance gain is 0.7%, wherein PASCAL-Person-Part dataset, the gain is 3.7%, and the PASCAL VOC 2012 dataset, it does not outperform human experts. (All measured by mIOU) Even though the push of the state-of-the-art is always something that worth celebrating, but in practice, one would argue after spending so many resources doing the search, the computer should achieve superhuman performance. (Like Chess Engine vs Chess Grand Master). In practice, one may simply go with the current state-of-the-art model to avoid the expensive search cost.
3. Still Heavily influenced by Human Bias
When we define the search space, we introduced human bias. Firstly, the network backbone is chosen from previous matured architectures, which may not actually be optimal. Secondly, the internal branches in the DPC also consist with layers whose operations are defined by us humans, and we define these operations based on previous experience. That also prevents the search algorithm to find something revolutionary.
4. May have the potential to take away entry-level data science jobs.
If there is a significant reduction in the search cost, it will be more cost effective to apply NAS rather than hire data scientists. Once matured, this technology will have the potential to take away entry-level data science jobs and make data science jobs only possessed by high-level researchers.
There are some real-world applications that already deploy NAS techniques in production. Two good examples are Google AutoML and Microsoft Custom Vision AI. [9, 10]
References
1. Searching For Efficient Multi-Scale Architectures For Dense Image Prediction, [[1]].
2. E. Real, A. Aggarwal, Y. Huang, and Q. V. Le. Regularized evolution for image classifier architecture search. arXiv:1802.01548, 2018.
3. C. Liu, B. Zoph, M. Neumann, J. Shlens, W. Hua, L.-J. Li, L. Fei-Fei, A. Yuille, J. Huang, and K. Murphy. Progressive neural architecture search. In ECCV, 2018.
4. B. Zoph, V. Vasudevan, J. Shlens, and Q. V. Le. Learning transferable architectures for scalable image recognition. In CVPR, 2018.
5. Neural Architecture Search: A Survey [[2]]
6. Deep Residual Learning for Image Recognition [[3]]
7. J. Long, E. Shelhamer, and T. Darrell. Fully convolutional networks for semantic segmentation. In CVPR, 2015. In the implementation wise, they used a Google vizier, which is a search tool for black box optimization. [D. Golovin, B. Solnik, S. Moitra, G. Kochanski, J. Karro, and D. Sculley. Google vizier: A service for black-box optimization. In SIGKDD, 2017.]
8. Github implementation of Google Vizer, a black-box optimization tool [4]
9. AutoML: https://cloud.google.com/automl/
10. Custom-vision: https://azure.microsoft.com/en-us/services/cognitive-services/custom-vision-service/
11. J. Dai, H. Qi, Y. Xiong, Y. Li, G. Zhang, H. Hu, and Y. Wei. Deformable convolutional networks. In ICCV, 2017.
12. M. Yang, K. Yu, C. Zhang, Z. Li, and K. Yang. Denseaspp for semantic segmentation in street scenes. In CVPR, 2018.