User:Yktan: Difference between revisions
(Replaced content with "== Presented by == Ruixian Chin, Yan Kai Tan, Jason Ong, Wen Cheen Chiew == Introduction == == Motivation == == Model Architecture == == Results == == Conclusio...") |
|||
| Line 8: | Line 8: | ||
== Motivation == | == Motivation == | ||
== Model Architecture == | == Model Architecture == | ||
DivideMix leverages semi-supervised learning to achieve effective modelling. The sample is first split into a labelled set and an unlabeled set. This is achieved by fitting a Gaussian Mixture Model as a per-sample loss distribution. The unlabeled set is made up of data points with discarded labels deemed noisy. Then, to avoid confirmation bias, which is typical when a model is self-training, two models are being trained simultaneously to filter error for each other. This is done by dividing the data using one model and then training the other model. This algorithm, known as Co-divide, keeps the two networks from converging when training, which avoids the bias from occurring. Figure 1 describes the algorithm in graphical form. | |||
[[File:ModelArchitecture.PNG | center]] | |||
<div align="center">Figure 1: Model Architecture of DivideMix</div> | |||
For each epoch, the network divides the dataset into a labelled set consisting of clean data, and an unlabeled set consisting of noisy data, which is then used as training data for the other network, where training is done in mini-batches. For each batch of the labelled samples, co-refinement is performed by using the ground truth label <math> y_b </math>, the predicted label <math> p_b </math>, and the posterior is used as the weight, <math> w_b </math>. | |||
<center><math> \bar{y}_b = w_b y_b + (1-w_b) p_b </math></center> | |||
Then, a sharpening function is implemented on this weighted sum to produce the estimate, <math> \hat{y}_b </math>. Using all these predicted labels, the unlabeled samples will then be assigned a "co-guessed" label, which should produce a more accurate prediction. Having calculated all these labels, MixMatch is applied to the combined mini-batch of labeled, <math> \hat{X} </math> and unlabeled data, <math> \hat{U} </math>, where, for a pair of samples and their labels, one new sample and new label is produced. More specifically, for a pair of samples <math> (x_1,x_2) </math> and their labels <math> (p_1,p_2) </math>, the mixed sample <math> (x',p') </math> is: | |||
<center> | |||
<math> | |||
\begin{alignat}{2} | |||
\lambda &\sim Beta(\alpha, \alpha) \\ | |||
\lambda ' &= max(\lambda, 1 - \lambda) \\ | |||
x' &= \lambda ' x_1 + (1 - \lambda ' ) x_2 \\ | |||
p' &= \lambda ' p_1 + (1 - \lambda ' ) p_2 \\ | |||
\end{alignat} | |||
</math> | |||
</center> | |||
MixMatch transforms <math> \hat{X} </math> and <math> \hat{U} </math> into <math> X' </math> and <math> U' </math>. Then, the loss on <math> X' </math>, <math> L_X </math> (Cross-entropy loss) and the loss on <math> U' </math>, <math> L_U </math> (Mean Squared Error) are calculated. A regularization term, <math> L_{reg} </math>, is introduced to regularize the model's average output across all samples in the mini-batch. Then, the total loss is calculated as: | |||
<center><math> L = L_X + \lambda_u L_U + \lambda_r L_{reg} </math></center> , | |||
where <math> \lambda_r </math> is set to 1, and <math> \lambda_u </math> is used to control the unsupervised loss. | |||
Lastly, the stochastic gradient descent formula is updated with the calculated loss, <math> L </math>, and the estimated parameters, <math> \boldsymbol{ \theta } </math>. | |||
== Results == | == Results == | ||
Revision as of 22:25, 2 November 2020
Presented by
Ruixian Chin, Yan Kai Tan, Jason Ong, Wen Cheen Chiew
Introduction
Motivation
Model Architecture
DivideMix leverages semi-supervised learning to achieve effective modelling. The sample is first split into a labelled set and an unlabeled set. This is achieved by fitting a Gaussian Mixture Model as a per-sample loss distribution. The unlabeled set is made up of data points with discarded labels deemed noisy. Then, to avoid confirmation bias, which is typical when a model is self-training, two models are being trained simultaneously to filter error for each other. This is done by dividing the data using one model and then training the other model. This algorithm, known as Co-divide, keeps the two networks from converging when training, which avoids the bias from occurring. Figure 1 describes the algorithm in graphical form.
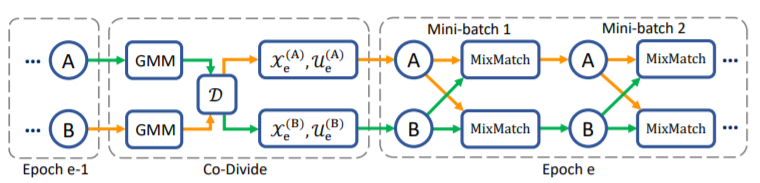
For each epoch, the network divides the dataset into a labelled set consisting of clean data, and an unlabeled set consisting of noisy data, which is then used as training data for the other network, where training is done in mini-batches. For each batch of the labelled samples, co-refinement is performed by using the ground truth label [math]\displaystyle{ y_b }[/math], the predicted label [math]\displaystyle{ p_b }[/math], and the posterior is used as the weight, [math]\displaystyle{ w_b }[/math].
Then, a sharpening function is implemented on this weighted sum to produce the estimate, [math]\displaystyle{ \hat{y}_b }[/math]. Using all these predicted labels, the unlabeled samples will then be assigned a "co-guessed" label, which should produce a more accurate prediction. Having calculated all these labels, MixMatch is applied to the combined mini-batch of labeled, [math]\displaystyle{ \hat{X} }[/math] and unlabeled data, [math]\displaystyle{ \hat{U} }[/math], where, for a pair of samples and their labels, one new sample and new label is produced. More specifically, for a pair of samples [math]\displaystyle{ (x_1,x_2) }[/math] and their labels [math]\displaystyle{ (p_1,p_2) }[/math], the mixed sample [math]\displaystyle{ (x',p') }[/math] is:
[math]\displaystyle{ \begin{alignat}{2} \lambda &\sim Beta(\alpha, \alpha) \\ \lambda ' &= max(\lambda, 1 - \lambda) \\ x' &= \lambda ' x_1 + (1 - \lambda ' ) x_2 \\ p' &= \lambda ' p_1 + (1 - \lambda ' ) p_2 \\ \end{alignat} }[/math]
MixMatch transforms [math]\displaystyle{ \hat{X} }[/math] and [math]\displaystyle{ \hat{U} }[/math] into [math]\displaystyle{ X' }[/math] and [math]\displaystyle{ U' }[/math]. Then, the loss on [math]\displaystyle{ X' }[/math], [math]\displaystyle{ L_X }[/math] (Cross-entropy loss) and the loss on [math]\displaystyle{ U' }[/math], [math]\displaystyle{ L_U }[/math] (Mean Squared Error) are calculated. A regularization term, [math]\displaystyle{ L_{reg} }[/math], is introduced to regularize the model's average output across all samples in the mini-batch. Then, the total loss is calculated as:
,
where [math]\displaystyle{ \lambda_r }[/math] is set to 1, and [math]\displaystyle{ \lambda_u }[/math] is used to control the unsupervised loss.
Lastly, the stochastic gradient descent formula is updated with the calculated loss, [math]\displaystyle{ L }[/math], and the estimated parameters, [math]\displaystyle{ \boldsymbol{ \theta } }[/math].