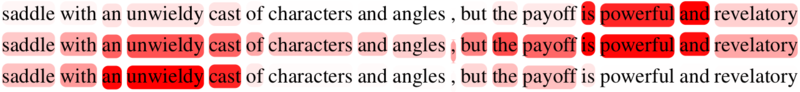User:Cvmustat
Combine Convolution with Recurrent Networks for Text Classification
Team Members: Bushra Haque, Hayden Jones, Michael Leung, Cristian Mustatea
Date: Week of Nov 23
Introduction
Previous Work
Paper Key Contributions
CRNN Results vs Benchmarks
CRNN Model Architecture
RNN Pipeline:
The goal of the RNN pipeline is to input each word in a text, and retrieve the contextual information surrounding the word and compute the contextual representation of the word itself. This is accomplished by use of a bi-directional RNN, such that a Neural Tensor Layer (NTL) can combine the results of the RNN to obtain the final output. RNNs are well-suited to NLP tasks because of their ability to sequentially process data such as ordered text.
A RNN is similar to a feed-forward neural network, but it relies on the use of hidden states. Hidden states are layers in the neural net that produce two outputs: [math]\displaystyle{ \hat{y}_{t} }[/math] and [math]\displaystyle{ h_t }[/math]. For a time step [math]\displaystyle{ t }[/math], [math]\displaystyle{ h_t }[/math] is fed back into the layer to compute [math]\displaystyle{ \hat{y}_{t+1} }[/math] and [math]\displaystyle{ h_{t+1} }[/math].
The pipeline will actually use a variant of RNN called GRU, short for Gated Recurrent Units. This is done to address the vanishing gradient problem which causes the network to struggle memorizing words that came earlier in the sequence. Traditional RNNs are only able to remember the most recent words in a sequence, which may be problematic since words that came in the beginning of the sequence that are important to the classification problem may be forgotten. A GRU attempts to solve this by controlling the flow of information through the network using update and reset gates.
Let [math]\displaystyle{ h_{t-1} \in \mathbb{R}^m, x_t \in \mathbb{R}^d }[/math] be the inputs, and let [math]\displaystyle{ \mathbf{W}_z, \mathbf{W}_r, \mathbf{W}_h \in \mathbb{R}^{m \times d}, \mathbf{U}_z, \mathbf{U}_r, \mathbf{U}_h \in \mathbb{R}^{m \times m} }[/math] be trainable weight matrices. Then the following equations describe the update and reset gates:
[math]\displaystyle{ z_t = \sigma(\mathbf{W}_zx_t + \mathbf{U}_zh_{t-1}) \text{update gate} \\ r_t = \sigma(\mathbf{W}_rx_t + \mathbf{U}_rh_{t-1}) \text{reset gate} \\ \tilde{h}_t = \text{tanh}(\mathbf{W}_hx_t + r_t \circ \mathbf{U}_hh_{t-1}) \text{new memory} \\ h_t = (1-z_t)\circ \tilde{h}_t + z_t\circ h_{t-1} }[/math]
Note that [math]\displaystyle{ \sigma, \text{tanh}, \circ }[/math] are all element-wise functions. The above equations do the following:
- [math]\displaystyle{ h_{t-1} }[/math] carries information from the previous iteration and [math]\displaystyle{ x_t }[/math] is the current input
- the update gate [math]\displaystyle{ z_t }[/math] controls how much past information should be forwarded to the next hidden state
- the rest gate [math]\displaystyle{ r_t }[/math] controls how much past information is forgotten or reset
- new memory [math]\displaystyle{ \tilde{h}_t }[/math] contains the relevant past memory as instructed by [math]\displaystyle{ r_t }[/math] and current information from the input [math]\displaystyle{ x_t }[/math]
- then [math]\displaystyle{ z_t }[/math] is used to control what is passed on from [math]\displaystyle{ h_{t-1} }[/math] and [math]\displaystyle{ (1-z_t) }[/math] controls the new memory that is passed on
Thus, each [math]\displaystyle{ h_t }[/math] can be computed as above to yield results for the bi-directional RNN.
CNN Pipeline:
The goal of the CNN pipeline is to learn the relative importance of words in an input sequence based on different aspects. The process of this CNN pipeline is summarized as the following steps:
- Given a sequence of words, each word is converted into a word vector using the word2vec algorithm which gives matrix X.
- Word vectors are then convolved through the temporal dimension with filters of various sizes (ie. different K) with learnable weights to capture various numerical K-gram representations. These K-gram representations are stored in matrix C.
- The convolution makes this process capture local and position-invariant features. Local means the K words are contiguous. Position-invariant means K contiguous words at any position are detected in this case via convolution.
- Temporal dimension example: convolve words from 1 to K, then convolve words 2 to K+1, etc
- Since not all K-gram representations are equally meaningful, there is a learnable matrix W which takes the linear combination of K-gram representations to more heavily weigh the more important K-gram representations for the classification task.
- Each linear combination of the K-gram representations gives the relative word importance based on the aspect that the linear combination encodes.
- The relative word importance vs aspect gives rise to an interpretable attention matrix A, where each element says the relative importance of a specific word for a specific aspect.
Merging RNN & CNN Pipeline Outputs
Interpreting Learned CRNN Weights
Recall that attention matrix A essentially stores the relative importance of every word in the input sequence for every aspect chosen. Naturally, this means that A is an n-by-z matrix, because n is the number of words in the input sequence and z is the number of aspects being considered in the classification task.
Furthermore, for a specific aspect, words with higher attention values are more important relative to other words in the same input sequence. For a specific word, aspects with higher attention values make the specific word more important compared to other aspects.
For example, in this paper, a sentence is sampled from the Movie Reviews dataset and the transpose of attention matrix A is visualized. Each word represents an element in matrix A, the intensity of red represents the magnitude of an attention value in A, and each sentence is the relative importance of each word for a specific context. In the first row, the words are weighted in terms of a positive aspect, in the last row, the words are weighted in terms of a negative aspect, and in the middle row, the words are weighted in terms of a positive and negative aspect. Notice how the relative importance of words is a function of the aspect.