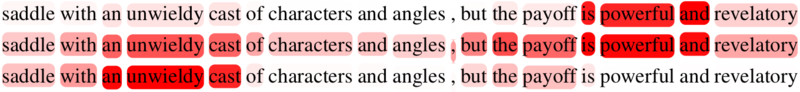User:Cvmustat
Combine Convolution with Recurrent Networks for Text Classification
Team Members: Bushra Haque, Hayden Jones, Michael Leung, Cristian Mustatea
Date: Week of Nov 23
Introduction
Text classification is the task of assigning a set of predefined categories to natural language texts. It is a fundamental task in Natural Language Processing (NLP) with various applications such as sentiment analysis, and topic classification. A classic example involving text classification is given a set of News articles, is it possible to classify the genre or subject of each article? Text classification is useful as text data is a rich source of information, but extracting insights from it directly can be difficult and time consuming as most text data is unstructured.[1] NLP text classification can help automatically structure and analyze text, quickly and cost-effectively, allowing for individuals to extract important features from the text easier than before.
In practice, pre-trained word embeddings and deep neural networks are used together for NLP text classification. Word embeddings are used to map the raw text data to an implicit space where the semantic relationships of the words are preserved; words with similar meaning have a similar representation. One can then feed these embeddings into deep neural networks to learn different features of the text. Convolutional neural networks can be used to determine the semantic composition of the text(the meaning), as it treats texts as a 2D matrix by concatenating embedding of words together, and it is able to capture both local and position invariant features of the text.[2] Alternatively, Recurrent Neural Networks can be used to determine the contextual meaning of each word in the text (how each word relates to one another) by treating the text as sequential data and then analyzing each word separately. [3] Previous approaches to attempt to combine these two neural networks to incorporate the advantages of both models involve streamlining the two networks, which might decrease their performance. In addition, most methods incorporating a bi-directional Recurrent Neural Network usually concatenate the forward and backward hidden states at each time step, which results in a vector that does not have the interaction information between the forward and backward hidden states.[4] The hidden state in one direction contains only the contextual meaning in that particular direction, however a word's contextual representation, intuitively, is more accurate when collected and viewed from both directions. This paper argues that the failure to observe the meaning of a word in both directions causes the loss of the true meaning of the word, especially for polysemic words (words with more than one meaning) that are context sensitive.
Paper Key Contributions
This paper suggests an enhanced method of text classification by proposing a new way of combining Convolutional and Recurrent Neural Networks involving the addition of a neural tensor layer. The proposed method maintains each network's respective strengths that are normally lost in previous combination methods. The new suggested architecture is called CRNN, which utilizes both a CNN and RNN that run in parallel on the same input sentence. The CNN uses weight matrix learning and produces a 2D matrix that shows the importance of each word based on local and position-invariant features. The bidirectional RNN produces a matrix that learns each word's contextual representation; the words' importance in relation to the rest of the sentence. A neural tensor layer is introduced on top of the RNN to obtain the fusion of bi-directional contextual information surrounding a particular word. The architecture combines these two matrix representations to classify the text as well as offer the importance information of each word for the prediction which can help with the interpretation of the results. The model also uses dropout and L2 regularization to prevent overfitting.
CRNN Results vs Benchmarks
In order to benchmark the performance of the CRNN model, as well as compare it to other previous efforts, multiple datasets and classification problems were used. All of these datasets are publicly available and can be easily downloaded by any user for testing.
Movie Reviews: a sentiment analysis dataset, with two classes (positive and negative).
Yelp: a sentiment analysis dataset, with five classes. For this test, a subset of 120,000 reviews was randomly chosen from each class for a total of 600,000 reviews.
AG's News: a news categorization dataset, using only the 4 largest classes from the dataset.
20 Newsgroups: a news categorization dataset, again using only 4 large classes from the dataset.
Sogou News: a Chinese news categorization dataset, using the 4 largest classes from the dataset.
Yahoo! Answers: a topic classification dataset, with 10 classes.
For the English language datasets, the initial word representations were created using the publicly available word2vec [1] from Google news. For the Chinese language dataset, jieba [2] was used to segment sentences, and then 50-dimensional word vectors were trained on Chinese wikipedia using word2vec.
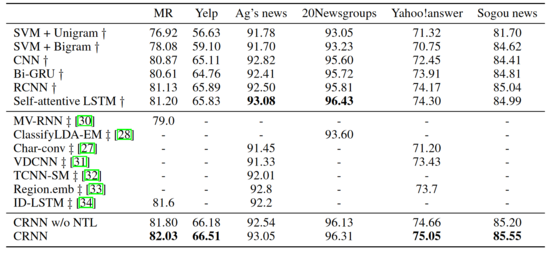
A number of other models are run against the same data after preprocessing, to obtain the following results:
The bold results represent the best performing model for a given dataset. These results show that the CRNN model manages to be the best performing in 4 of the 6 datasets, with the Self-attentive LSTM beating the CRNN by 0.03 and 0.12 on the news categorization problems. Considering that the CRNN model has better performance than the Self-attentive LSTM on the other 4 datasets, this suggests that the CRNN model is a better performer overall in the conditions of this benchmark.
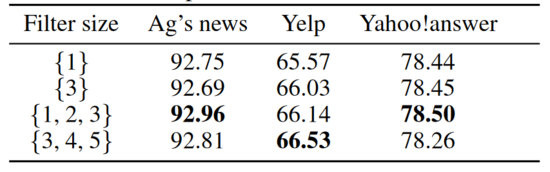
Another important result was that the CRNN model filter size impacted performance only in the sentiment analysis datasets, as seen in the following:
CRNN Model Architecture
RNN Pipeline:
The goal of the RNN pipeline is to input each word in a text, and retrieve the contextual information surrounding the word and compute the contextual representation of the word itself. This is accomplished by use of a bi-directional RNN, such that a Neural Tensor Layer (NTL) can combine the results of the RNN to obtain the final output. RNNs are well-suited to NLP tasks because of their ability to sequentially process data such as ordered text.
A RNN is similar to a feed-forward neural network, but it relies on the use of hidden states. Hidden states are layers in the neural net that produce two outputs: [math]\displaystyle{ \hat{y}_{t} }[/math] and [math]\displaystyle{ h_t }[/math]. For a time step [math]\displaystyle{ t }[/math], [math]\displaystyle{ h_t }[/math] is fed back into the layer to compute [math]\displaystyle{ \hat{y}_{t+1} }[/math] and [math]\displaystyle{ h_{t+1} }[/math].
The pipeline will actually use a variant of RNN called GRU, short for Gated Recurrent Units. This is done to address the vanishing gradient problem which causes the network to struggle memorizing words that came earlier in the sequence. Traditional RNNs are only able to remember the most recent words in a sequence, which may be problematic since words that came at the beginning of the sequence that are important to the classification problem may be forgotten. A GRU attempts to solve this by controlling the flow of information through the network using update and reset gates.
Let [math]\displaystyle{ h_{t-1} \in \mathbb{R}^m, x_t \in \mathbb{R}^d }[/math] be the inputs, and let [math]\displaystyle{ \mathbf{W}_z, \mathbf{W}_r, \mathbf{W}_h \in \mathbb{R}^{m \times d}, \mathbf{U}_z, \mathbf{U}_r, \mathbf{U}_h \in \mathbb{R}^{m \times m} }[/math] be trainable weight matrices. Then the following equations describe the update and reset gates:
[math]\displaystyle{ z_t = \sigma(\mathbf{W}_zx_t + \mathbf{U}_zh_{t-1}) \text{update gate} \\ r_t = \sigma(\mathbf{W}_rx_t + \mathbf{U}_rh_{t-1}) \text{reset gate} \\ \tilde{h}_t = \text{tanh}(\mathbf{W}_hx_t + r_t \circ \mathbf{U}_hh_{t-1}) \text{new memory} \\ h_t = (1-z_t)\circ \tilde{h}_t + z_t\circ h_{t-1} }[/math]
Note that [math]\displaystyle{ \sigma, \text{tanh}, \circ }[/math] are all element-wise functions. The above equations do the following:
- [math]\displaystyle{ h_{t-1} }[/math] carries information from the previous iteration and [math]\displaystyle{ x_t }[/math] is the current input
- the update gate [math]\displaystyle{ z_t }[/math] controls how much past information should be forwarded to the next hidden state
- the rest gate [math]\displaystyle{ r_t }[/math] controls how much past information is forgotten or reset
- new memory [math]\displaystyle{ \tilde{h}_t }[/math] contains the relevant past memory as instructed by [math]\displaystyle{ r_t }[/math] and current information from the input [math]\displaystyle{ x_t }[/math]
- then [math]\displaystyle{ z_t }[/math] is used to control what is passed on from [math]\displaystyle{ h_{t-1} }[/math] and [math]\displaystyle{ (1-z_t) }[/math] controls the new memory that is passed on
We treat [math]\displaystyle{ h_0 }[/math] and [math]\displaystyle{ h_{n+1} }[/math] as zero vectors in the method. Thus, each [math]\displaystyle{ h_t }[/math] can be computed as above to yield results for the bi-directional RNN. The resulting hidden states [math]\displaystyle{ \overrightarrow{h_t} }[/math] and [math]\displaystyle{ \overleftarrow{h_t} }[/math] contain contextual information around the [math]\displaystyle{ t }[/math]-th word in forward and backward directions respectively. Contrary to convention, instead of concatenating these two vectors, it is argued that the word's contextual representation is more precise when the context information from different directions is collected and fused using a neural tensor layer as it permits greater interactions among each element of hidden states. Using these two vectors as input to the neural tensor layer, [math]\displaystyle{ V^i }[/math], we compute a new representation that aggregates meanings from the forward and backward hidden states more accurately as follows:
[math]\displaystyle{ [\hat{h_t}]_i = tanh(\overrightarrow{h_t}V^i\overleftarrow{h_t} + b_i) }[/math]
Where [math]\displaystyle{ V^i \in \mathbb{R}^{m \times m} }[/math] is the learned tensor layer, and [math]\displaystyle{ b_i \in \mathbb{R} }[/math] is the bias.We repeat this [math]\displaystyle{ m }[/math] times with different [math]\displaystyle{ V^i }[/math] matrices and [math]\displaystyle{ b_i }[/math] vectors. Through the neural tensor layer, each element in [math]\displaystyle{ [\hat{h_t}]_i }[/math] can be viewed as a different type of intersection between the forward and backward hidden states. In the model, [math]\displaystyle{ [\hat{h_t}]_i }[/math] will have the same size as the forward and backward hidden states. We then concatenate the three hidden states vectors to form a new vector that summarizes the context information : [math]\displaystyle{ \overleftrightarrow{h_t} = [\overrightarrow{h_t}^T,\overleftarrow{h_t}^T,\hat{h_t}]^T }[/math]
We calculate this vector for every word in the text and then stack them all into matrix [math]\displaystyle{ H }[/math] with shape [math]\displaystyle{ n }[/math]-by-[math]\displaystyle{ 3m }[/math].
[math]\displaystyle{ H = [\overleftrightarrow{h_1};...\overleftrightarrow{h_n}] }[/math]
This [math]\displaystyle{ H }[/math] matrix is then forwarded as the results from the Recurrent Neural Network.
CNN Pipeline:
The goal of the CNN pipeline is to learn the relative importance of words in an input sequence based on different aspects. The process of this CNN pipeline is summarized as the following steps:
- Given a sequence of words, each word is converted into a word vector using the word2vec algorithm which gives matrix X.
- Word vectors are then convolved through the temporal dimension with filters of various sizes (ie. different K) with learnable weights to capture various numerical K-gram representations. These K-gram representations are stored in matrix C.
- The convolution makes this process capture local and position-invariant features. Local means the K words are contiguous. Position-invariant means K contiguous words at any position are detected in this case via convolution.
- Temporal dimension example: convolve words from 1 to K, then convolve words 2 to K+1, etc
- Since not all K-gram representations are equally meaningful, there is a learnable matrix W which takes the linear combination of K-gram representations to more heavily weigh the more important K-gram representations for the classification task.
- Each linear combination of the K-gram representations gives the relative word importance based on the aspect that the linear combination encodes.
- The relative word importance vs aspect gives rise to an interpretable attention matrix A, where each element says the relative importance of a specific word for a specific aspect.
Merging RNN & CNN Pipeline Outputs
The results from both the RNN and CNN pipeline can be merged by simply multiplying the output matrices. That is, we compute [math]\displaystyle{ S=A^TH }[/math] which has shape [math]\displaystyle{ z \times 3m }[/math] and is essentially a linear combination of the hidden states. The concatenated rows of S results in a vector in [math]\displaystyle{ \mathbb{R}^{3zm} }[/math], and can be passed to a fully connected Softmax layer to output a vector of probabilities for our classification task.
To train the model, we make the following decisions:
- Use cross-entropy loss as the loss function
- Perform dropout on random columns in matrix C in the CNN pipeline
- Perform L2 regularization on all parameters
- Use stochastic gradient descent with a learning rate of 0.001
Interpreting Learned CRNN Weights
Recall that attention matrix A essentially stores the relative importance of every word in the input sequence for every aspect chosen. Naturally, this means that A is an n-by-z matrix, with n being the number of words in the input sequence and z being the number of aspects considered in the classification task.
Furthermore, for any specific aspect, words with higher attention values are more important relative to other words in the same input sequence. likewise, for any specific word, aspects with higher attention values prioritize the specific word more than other aspects.
For example, in this paper, a sentence is sampled from the Movie Reviews dataset and the transpose of attention matrix A is visualized. Each word represents an element in matrix A, the intensity of red represents the magnitude of an attention value in A, and each sentence is the relative importance of each word for a specific context. In the first row, the words are weighted in terms of a positive aspect, in the last row, the words are weighted in terms of a negative aspect, and in the middle row, the words are weighted in terms of a positive and negative aspect. Notice how the relative importance of words is a function of the aspect.
Conclusion & Summary
This paper proposed a new architecture, the Convolutional Recurrent Neural Network, for text classification. The Convolutional Neural Network is used to learn the relative importance of each word from different aspects and stores it into a weight matrix. The Recurrent Neural Network learns each words contextual representation through the combination of the forward and backward context informations that are fused using a neural tensor layer and is stored as a matrix. These two matrices are then combined to get the text representation used for classification. Although the specifics of the performed tests are lacking, the experiment's results indicate that the proposed method performed well in comparison to most previous methods. In addition to performing well, the proposed method also provides insight into which words contribute greatly to the classification decision as the learned matrix from the Convolutional Neural Network stores the relative importance of each word. This information can then be used in other applications or analysis. In the future, one can explore the features that extracted from the model and use them to potentially learn new methods such as model space. [5]
Critiques
In the Method section of the paper, some explanations used the same notation for multiple different elements of the model. This made the paper harder to follow and understand since they were referring to different elements by identical notation.
In Comparison of Methods, the authors discuss the range of hyperparameter settings that they search through. While some of the hyperparameters have a large range of search values, three parameters are fixed without much explanation as to why for all experiments, size of the hidden state of GRU, number of layers, and dropout. These parameters have a lot to do with the complexity of the model and this paper could be improved by providing relevant reasoning behind these values, or by providing additional experimental results over different values of these parameters.
In the Results section of the paper, they tried to show that the classification results from the CRNN model can be better interpreted than other models. In these explanations, the details were lacking and the authors did not adequately demonstrate how their model is better than others.
Finally, in the Results section again, the paper compares the CRNN model to several models which they did not implement and reproduce results with. This can be seen in the chart of results above, where several models do not have entries in the table for all six datasets. Since the authors used a subset of the datasets, these other models which were not reproduced could have different accuracy scores if they had been tested on the same data as the CRNN model. This difference in training and testing data is not mentioned in the paper, and the conclusion that the CRNN model is better in all cases may not be valid.
- Could this be applied to hieroglyphs to decipher/better understand them?
References
[1] Grimes, Seth. “Unstructured Data and the 80 Percent Rule.” Breakthrough Analysis, 1 Aug. 2008, breakthroughanalysis.com/2008/08/01/unstructured-data-and-the-80-percent-rule/.
[2] N. Kalchbrenner, E. Grefenstette, and P. Blunsom, “A convolutional neural network for modelling sentences,” arXiv preprint arXiv:1404.2188, 2014.
[3] K. Cho, B. V. Merri¨enboer, C. Gulcehre, D. Bahdanau, F. Bougares, H. Schwenk, and Y. Bengio, “Learning phrase representations using RNN encoder-decoder for statistical machine translation,” arXiv preprint arXiv:1406.1078, 2014.
[4] S. Lai, L. Xu, K. Liu, and J. Zhao, “Recurrent convolutional neural networks for text classification,” in Proceedings of AAAI, 2015, pp. 2267–2273.
[5] H. Chen, P. Tio, A. Rodan, and X. Yao, “Learning in the model space for cognitive fault diagnosis,” IEEE Transactions on Neural Networks and Learning Systems, vol. 25, no. 1, pp. 124–136, 2014.