The Curious Case of Degeneration: Difference between revisions
| Line 34: | Line 34: | ||
The goal of the open-ended tasks is to generate the next n continuation tokens given a context sequence with m tokens. That is to maximize the following probability. | The goal of the open-ended tasks is to generate the next n continuation tokens given a context sequence with m tokens. That is to maximize the following probability. | ||
\begin{align} | |||
P(x_{1:m+n})=\prod_{i=1}^{m+n}P(x_i|x_1 \ldots x_{i-1}) | |||
\end{align} | |||
====Nucleus Sampling==== | ====Nucleus Sampling==== | ||
This decoding strategy is indeed truncating the long tail of the probability distribution. In order to do that, first, we need to find the smallest vocabulary set <math>V^{(p)}</math> which satisfies <math>\Sigma_{x \in V^{(p)}} P(x|x_{1:i-1}) \ge p</math>. Then set <math>p'=\Sigma_{x \in V^{(p)}} P(x|x_{1:i-1}) \ge p</math> and rescale the probability distribution with <math>p'</math> and select the tokens from <math>P'</math>. | This decoding strategy is indeed truncating the long tail of the probability distribution. In order to do that, first, we need to find the smallest vocabulary set <math>V^{(p)}</math> which satisfies <math>\Sigma_{x \in V^{(p)}} P(x|x_{1:i-1}) \ge p</math>. Then set <math>p'=\Sigma_{x \in V^{(p)}} P(x|x_{1:i-1}) \ge p</math> and rescale the probability distribution with <math>p'</math> and select the tokens from <math>P'</math>. | ||
Revision as of 20:06, 14 November 2020
Presented by
Donya Hamzeian
Introduction
Text generation is the act of automatically generating natural language texts like summarization, neural machine translation, fake news generation and etc. Degeneration happens when the output text is incoherent or produces repetitive results. For example in the figure below, the GPT2 model tries to generate the continuation text given the context. On the left side, the beam-search was used as the decoding strategy which has obviously stuck in a repetitive loop. On the right side, however, you can see how the pure sampling decoding strategy has generated incoherent results.

As a quick recap, the beam search is a best-first search algorithm. At each step, it selects the K most-probable predictions, where K is the beam width parameter set by humans. If K is 1, the beam search algorithm becomes the greedy search algorithm, where only the best prediction is picked. In beam search, the system only explores K paths, which reduces the memory requirements.
The authors argue that decoding strategies that are based on maximization like beam search lead to degeneration even with powerful models like GPT-2. Even though there are some utility functions that encourage diversity, they are not enough and the text generated by maximization, beam-search, or top-k sampling is too probable which indicates the lack of diversity (variance) compared to human-generated texts
Others have questioned whether a problem with beam search is that by expanding on only the top k tokens in each step of the generation, in later steps it may miss possible sequence that would have resulted in a more probable overall phrase. The authors argue that this isn't an issue for generating natural language as it has lower per-token probability on average and people usually optimize against saying the obvious.
The authors blame the long, unreliable tail in the probability distribution of tokens that the model samples from i.e. vocabularies with low probability frequently appear in the output text. So, top-k sampling with high values of k may produce texts closer to human texts, yet they have high variance in likelihood leading to incoherency issues. Therefore, instead of fixed k, it is good to dynamically increase or decrease the number of candidate tokens. Nucleus Sampling which is the contribution of this paper does this expansion and contraction of the candidate pool.
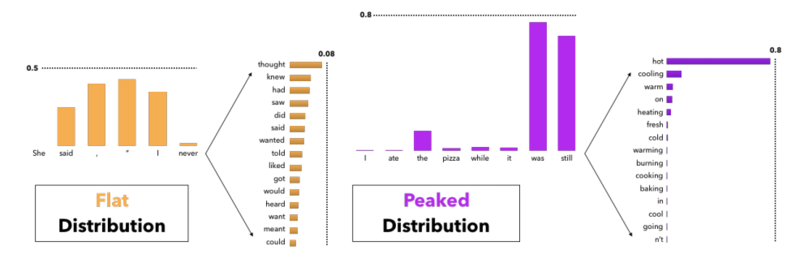
The problem with a fixed k
In the figure below, it can be seen why having a fixed k in the top-k sampling decoding strategy can lead to degenerative results, more specifically, incoherent and low diversity texts. For instance, in the left figure, the distribution of the next token is flat i.e. there are many tokens with nearly equal probability to be the next token. In this case, if we choose a small k, like 5, some tokens like "meant" and "want" may not appear in the generated text which makes it less diverse. On the other hand, in the right figure, the distribution of the next token is peaked, i.e there are very few words with very high probability. In this case, if we choose k to be large, like 10, we may end up choosing tokens like "going" and "n't" which makes the generated text incoherent. Therefore, it seems that having a fixed-k may lead to degeneration
Language Model Decoding
There are two types of generation tasks.
1. Directed generation tasks: In these tasks, there are pairs of (input, output), where the model tries to generate the output text which is tightly scoped by the input text. Due to this constraint, these tasks suffer less from the degeneration. Summarization, neural machine translation, and input-to-text generation are some examples of these tasks.
2. Open-ended generation tasks like conditional story generation or like the tasks in the above figure have high degrees of freedom. As a result, degeneration is more frequent in these tasks and the focus of this paper.
The goal of the open-ended tasks is to generate the next n continuation tokens given a context sequence with m tokens. That is to maximize the following probability.
\begin{align} P(x_{1:m+n})=\prod_{i=1}^{m+n}P(x_i|x_1 \ldots x_{i-1}) \end{align}
Nucleus Sampling
This decoding strategy is indeed truncating the long tail of the probability distribution. In order to do that, first, we need to find the smallest vocabulary set [math]\displaystyle{ V^{(p)} }[/math] which satisfies [math]\displaystyle{ \Sigma_{x \in V^{(p)}} P(x|x_{1:i-1}) \ge p }[/math]. Then set [math]\displaystyle{ p'=\Sigma_{x \in V^{(p)}} P(x|x_{1:i-1}) \ge p }[/math] and rescale the probability distribution with [math]\displaystyle{ p' }[/math] and select the tokens from [math]\displaystyle{ P' }[/math]. [math]\displaystyle{ P'(x|x_{1:i-1}) = \begin{cases} \frac{P(x|x_{1:i-1})}{p'}, & \mbox{if } x \in V^{(p)} \\ 0 & \mbox{if } otherwise \end{cases} }[/math]
Top-k Sampling
Top-k sampling also relies on truncating the distribution. In this decoding strategy, we need to first find a set of tokens with size [math]\displaystyle{ k }[/math], [math]\displaystyle{ V^{(k)} }[/math], which maximizes [math]\displaystyle{ \Sigma_{x \in V^{(k)}} P(x|x_{1:i-1}) }[/math] and set [math]\displaystyle{ p' = \Sigma_{x \in V^{(k)}} P(x|x_{1:i-1}) }[/math]. Finally, rescale the probability distribution similar to the Nucleus sampling.
Intuitively, the difference between Top-k sampling and Nucleus sampling is how they set a threshold of truncation - the former one defines a threshold at which the tail of the probability distribution gets truncated, whereas the latter puts a cap the number of tokens in the vocabulary set. It is noteworthy that thresholding the number of tokens can cause [math]\displaystyle{ p' }[/math] to fluctuate greatly at different time steps.
Sampling with Temperature
In this method, which was proposed in [1], the probability of tokens are calculated according to the equation below where [math]\displaystyle{ t \in (0,1) }[/math] is the temperature and [math]\displaystyle{ u_{1:|V|} }[/math] are logits.
[math]\displaystyle{ P(x= V_l|x_{1:i-1}) = \frac{\exp(\frac{u_l}{t})}{\Sigma_{l'}\exp(\frac{u'_l}{t})} }[/math]
Recent studies have shown that lowering [math]\displaystyle{ t }[/math] improves the quality of the generated texts while it decreases diversity. Note that the temperature [math]\displaystyle{ t }[/math] controls how conservative the model is, and this analogy comes from thermodynamics, where lower temperature means lower energy states are unlikely to be encountered. Hence, the lower the temperature, the less likely the model is to sample tokens with lower probability.
Likelihood Evaluation
To see the results of the nucleus decoding strategy, they used GPT2-large that was trained on WebText to generate 5000 text documents conditioned on initial paragraphs with 1-40 tokens.
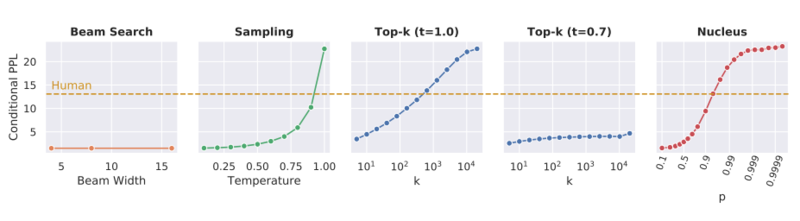
Perplexity
This score was used to compare the coherence of different decoding strategies. By looking at the graphs below, it is possible for Sampling, Top-k sampling, and Nucleus strategies to be tuned such that they achieve a perplexity close to the perplexity of human-generated texts; however, with the best parameters according to the perplexity the first two strategies generate low diversity texts.
What is Perplexity?
Perplexity as previously mentioned is a score that comes from information theory [3]. It is a measure of how well a probabilistic model or distribution predicts a sample. This intuitively leads to it being useful for comparing how competition models explain the same sample or dataset. Perplexity has close ties to information entropy as can be seen in the following discrete formulation of perplexity for a probability distribution.
- [math]\displaystyle{ PP(p) := 2^{H(p)}=2^{-\sum_x p(x)\log_2 p(x)} }[/math]
Here [math]\displaystyle{ H(p) }[/math] is the entropy in bits and [math]\displaystyle{ p(x) }[/math] is the probability of observing [math]\displaystyle{ x }[/math] from the distribution.
Perplexity in the context of probability models also has close ties to information entropy. The idea here is a model [math]\displaystyle{ f(x) }[/math] is fit to data from an unknown probability distribution [math]\displaystyle{ p(x) }[/math]. When the model is given test samples which were not used during its construction; the model will assign these samples some probability [math]\displaystyle{ f(x_i) }[/math]. Here [math]\displaystyle{ x_i }[/math] comes from a test set where [math]\displaystyle{ i = 1,...,N }[/math]. The perplexity will be lowest for a model which has high probabilities for the test samples. This can be seen in the following equation:
- [math]\displaystyle{ PPL = b^{- \frac{1}{N} \sum_{i=1}^N \log_b q(x_i)} }[/math]
Here [math]\displaystyle{ b }[/math] is the base and can be any number though commonly 2 is used to represent bits.
Distributional Statistical Evaluation
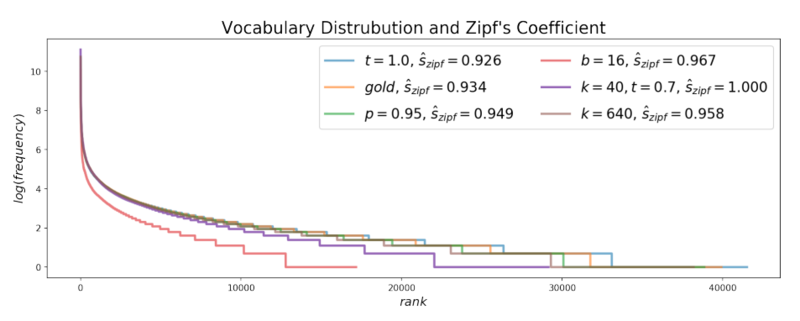
Zipf Distribution Analysis
Zipf's law says that the frequency of any word is inversely proportional to its rank in the frequency table, so it suggests that there is an exponential relationship between the rank of each word with its frequency in the text. By looking at the graph below, it seems that the Zipf's distribution of the texts generated with Nucleus sampling is very close to the Zipf's distribution of the human-generated(gold) texts, while beam-search is very different from them.
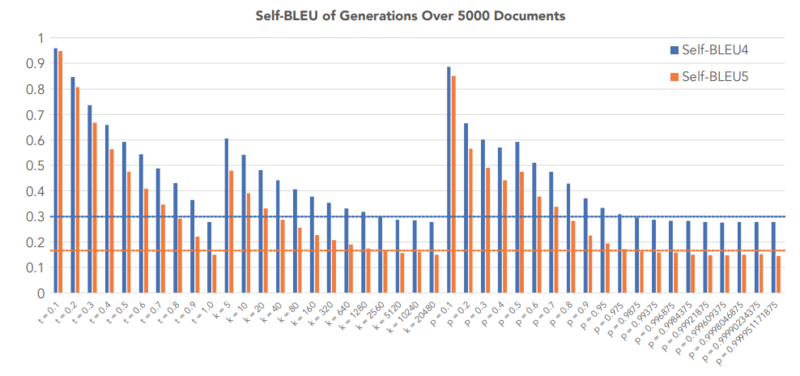
Self BLEU
The Self-BLEU score[2] is used to compare the diversity of each decoding strategy and was computed for each generated text using all other generations in the evaluation set as references. In the figure below, the self-BLEU score of three decoding strategies- Top-K sampling, Sampling with Temperature, and Nucleus sampling- were compared against the Self-BLEU of human-generated texts. By looking at the figure below, we see that high values of parameters that generate the self-BLEU close to that of the human texts result in incoherent, low perplexity, in Top-K sampling and Temperature Sampling, while this is not the case for Nucleus sampling.
Conclusion
In this paper, different decoding strategies were analyzed on open-ended generation tasks. They showed that likelihood maximization decoding causes degeneration where decoding strategies which rely on truncating the probability distribution of tokens especially Nucleus sampling can produce coherent and diverse texts close to human-generated texts.
References
[1]: David H Ackley, Geoffrey E Hinton, and Terrence J Sejnowski. A learning algorithm for boltzmann machines. Cognitive science, 9(1):147–169, 1985.
[2]: Yaoming Zhu, Sidi Lu, Lei Zheng, Jiaxian Guo, Weinan Zhang, Jun Wang, and Yong Yu. Texygen: A benchmarking platform for text generation models. SIGIR, 2018
[3]: Perplexity: https://en.wikipedia.org/wiki/Perplexity