Task Understanding from Confusing Multi-task Data: Difference between revisions
| Line 167: | Line 167: | ||
- It would be interesting to see this implemented in more examples, to test the robustness to different types of data. | - It would be interesting to see this implemented in more examples, to test the robustness to different types of data. | ||
Even though this paper has already included some examples when testing the CSL in experiments, it will be better to include more detailed examples for partial-label in the "Application of Multi-label Learning" section. | |||
= References = | = References = | ||
Revision as of 23:17, 23 November 2020
Presented By
Qianlin Song, William Loh, Junyue Bai, Phoebe Choi
Introduction
Narrow AI is an artificial intelligence that outperforms human in a narrowly defined task. The application of Narrow AI is becoming more and more common. For example, Narrow AI can be used for spam filtering, music recommendation services, and even self-driving cars. However, the widespread use of Narrow AI in important infrastructure functions raises some concerns. Some people think that the characteristics of Narrow AI make it fragile, and when neural networks can be used to control important systems (such as power grids, financial transactions), alternatives may be more inclined to avoid risks.While these machines help companies improve efficiency and cut costs, the limitations of Narrow AI encouraged researchers to look into General AI.
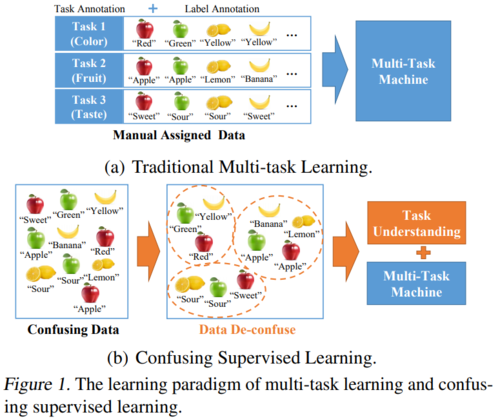
General AI is a machine that can apply its learning to different contexts, which closely resembles human intelligence. This paper attempts to generalize the multi-task learning system, a system that allows the machine to learn from data from multiple classification tasks. One application is image recognition. In figure 1, an image of an apple corresponds to 3 labels: “red”, “apple” and “sweet”. These labels correspond to 3 different classification tasks: color, fruit, and taste.
Currently, multi-task machines require researchers to construct a task definition. Otherwise, it will end up with different outputs with the same input value. Researchers manually assign tasks to each input in the sample to train the machine. See figure 1(a). This method incurs high annotation costs and restricts the machine’s ability to mirror the human recognition process. This paper is interested in developing an algorithm that understands task concepts and performs multi-task learning without manual task annotations.
This paper proposed a new learning method called confusing supervised learning (CSL) which includes 2 functions: de-confusing function and mapping function. The first function allocates identifies an input to its respective task and the latter finds the relationship between the input and its label. See figure 1(b). To train a network of CSL, CSL-Net is constructed for representing CSL’s variables. However, this structure cannot be optimized by gradient back-propagation. This difficulty is solved by alternatively performing training for the de-confusing net and mapping net optimization.
Experiments for function regression and image recognition problems were constructed and compared with multi-task learning with complete information to test CSL-Net’s performance. Experiment results show that CSL-Net can learn multiple mappings for every task simultaneously and achieve the same cognition result as the current multi-task machine sigh complete information.
Related Work
Multi-task learning
Multi-task learning aims to learn multiple tasks simultaneously using a shared feature representation. In multi-task learning, the task to which every sample belongs is known. By exploiting similarities and differences between tasks, the learning from one task can improve the learning of another task. (Caruana, 1997) This results in improved learning efficiency. Multi-task learning is used in disciplines like computer vision, natural language processing, and reinforcement learning. It requires manual task annotation to learn and this paper is interested in machine learning without a clear task definition and manual task annotation.
Latent variable learning
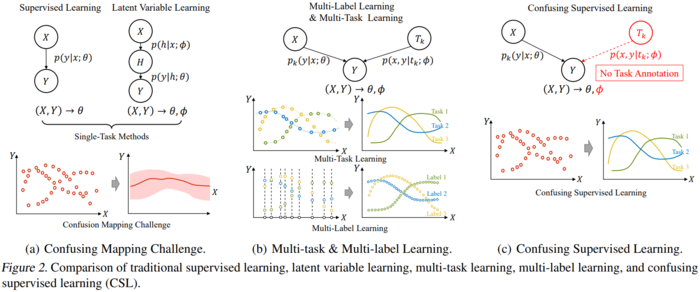
Latent variable learning aims to estimate the true function with mixed probability models. See figure 2a. In the multi-task learning problem without task annotations, samples are generated from multiple distributions instead of one distribution. Thus, latent variable learning is insufficient to solve the research problem, which is multi-task confusing samples.
Multi-label learning
Multi-label learning aims to assign an input to a set of classes/labels. See figure 2b. It is a generalization of multi-class classification, which classifies an input into one class. In multi-label learning, an input can be classified into more than one class. Unlike multi-task learning, multi-label does not consider the relationship between different label judgments and it is assumed that each judgment is independent. An example where multi-label learning is applicable is the scenario where a website wants to automatically assign applicable tags/categories to an article. Since an article can be related to multiple categories (eg. an article can be tagged under the politics and business categories) multi-label learning is of primary concern here.
Confusing Supervised Learning
Description of the Problem
Confusing supervised learning (CSL) offers a solution to the issue at hand. A major area of improvement can be seen in the choice of risk measure. In traditional supervised learning, assuming the risk measure is mean squared error (MSE), the expected risk functional is
$$ R(g) = \int_x (f(x) - g(x))^2 p(x) \; \mathrm{d}x $$
where [math]\displaystyle{ p(x) }[/math] is the prior distribution of the input variable [math]\displaystyle{ x }[/math]. In practice, model optimizations are performed using the empirical risk
$$ R_e(g) = \sum_{i=1}^n (y_i - g(x_i))^2 $$
When the problem involves different tasks, the model should optimize for each data point depending on the given task. Let [math]\displaystyle{ f_j(x) }[/math] be the true ground-truth function for each task [math]\displaystyle{ j }[/math]. Therefore, for some input variable [math]\displaystyle{ x_i }[/math], an ideal model [math]\displaystyle{ g }[/math] would predict [math]\displaystyle{ g(x_i) = f_j(x_i) }[/math]. With this, the risk functional can be modified to fit this new task for traditional supervised learning methods.
$$ R(g) = \int_x \sum_{j=1}^n (f_j(x) - g(x))^2 p(f_j) p(x) \; \mathrm{d}x $$
We call [math]\displaystyle{ (f_j(x) - g(x))^2 p(f_j) }[/math] the confusing multiple mappings. Then the optimal solution [math]\displaystyle{ g^*(x) }[/math] to the mapping is [math]\displaystyle{ \bar{f}(x) = \sum_{j=1}^n p(f_j) f_j(x) }[/math] under this risk functional. However, the optimal solution is not conditional on the specific task at hand but rather on the entire ground-truth functions. Therefore, for every non-trivial set of tasks where [math]\displaystyle{ f_u(x) \neq f_v(x) }[/math] for some input [math]\displaystyle{ x }[/math] and [math]\displaystyle{ u \neq v }[/math], [math]\displaystyle{ R(g^*) \gt 0 }[/math] which implies that there is an unavoidable confusion risk.
Learning Functions of CSL
To overcome this issue, the authors introduce two types of learning functions:
- Deconfusing function — allocation of which samples come from the same task
- Mapping function — mapping relation from input to output of every learned task
Suppose there are [math]\displaystyle{ n }[/math] ground-truth mappings [math]\displaystyle{ \{f_j : 1 \leq j \leq n\} }[/math] that we wish to approximate with a set of mapping functions [math]\displaystyle{ \{g_k : 1 \leq k \leq l\} }[/math]. The authors define the deconfusing function as an indicator function [math]\displaystyle{ h(x, y, g_k) }[/math] which takes some sample [math]\displaystyle{ (x,y) }[/math] and determines whether the sample is assigned to task [math]\displaystyle{ g_k }[/math]. Under the CSL framework, the risk functional (mean squared loss) is
$$ R(g,h) = \int_x \sum_{j,k} (f_j(x) - g_k(x))^2 \; h(x, f_j(x), g_k) \;p(f_j) \; p(x) \;\mathrm{d}x $$
which can be estimated empirically with
$$R_e(g,h) = \sum_{i=1}^m \sum_{k=1}^n |y_i - g_k(x_i)|^2 \cdot h(x_i, y_i, g_k) $$
Theoretical Results
This novel framework yields some theoretical results to show the viability of its construction.
Theorem 1 (Existence of Solution) With the confusing supervised learning framework, there is an optimal solution $$h^*(x, f_j(x), g_k) = \mathbb{I}[j=k]$$
$$g_k^*(x) = f_k(x)$$
for each [math]\displaystyle{ k=1,..., n }[/math] that makes the expected risk function of the CSL problem zero.
Theorem 2 (Error Bound of CSL) With probability at least [math]\displaystyle{ 1 - \eta }[/math] simultaneously with finite VC dimension [math]\displaystyle{ \tau }[/math] of CSL learning framework, the risk measure is bounded by
$$R(\alpha) \leq R_e(\alpha) + \frac{B\epsilon(m)}{2} \left(1 + \sqrt{1 + \frac{4R_e(\alpha)}{B\epsilon(m)}}\right)$$
where [math]\displaystyle{ \alpha }[/math] is the total parameters of learning functions [math]\displaystyle{ g, h }[/math], [math]\displaystyle{ B }[/math] is the upper bound of one sample's risk, [math]\displaystyle{ m }[/math] is the size of training data and $$\epsilon(m) = 4 \; \frac{\tau (\ln \frac{2m}{\tau} + 1) - \ln \eta / 4}{m}$$
CSL-Net
In this section the authors describe how to implement and train a network for CSL.
The Structure of CSL-Net
Two neural networks, deconfusing-net and mapping-net are trained to implement two learning function variables in empirical risk. The optimization target of the training algorithm is: $$\min_{g, h} R_e = \sum_{i=1}^{m}\sum_{k=1}^{n} (y_i - g_k(x_i))^2 \cdot h(x_i, y_i; g_k)$$
The mapping-net is corresponding to functions set [math]\displaystyle{ g_k }[/math], where [math]\displaystyle{ y_k = g_k(x) }[/math] represents the output of one certain task. The deconfusing-net is corresponding to function h, whose input is a sample [math]\displaystyle{ (x,y) }[/math] and output is an n-dimensional one-hot vector. This output vector determines which task the sample [math]\displaystyle{ (x,y) }[/math] should be assigned to. The core difficulty of this algorithm is that the risk function cannot be optimized by gradient back-propagation due to the constraint of one-hot output from deconfusing-net. Approximation of softmax will lead the deconfusing-net output into a non-one-hot form, which resulting in meaningless trivial solutions.
Iterative Deconfusing Algorithm
To overcome the training difficulty, the authors divide the empirical risk minimization into two local optimization problems. In each single-network optimization step, the parameters of one network is updated while the parameters of another remain fixed. With one network's parameters unchanged, the problem can be solved by a gradient descent method of neural networks.
Training of Mapping-Net: With function h from deconfusing-net being determined, the goal is to train every mapping function [math]\displaystyle{ g_k }[/math] with its corresponding sample [math]\displaystyle{ (x_i^k, y_i^k) }[/math]. The optimization problem becomes: [math]\displaystyle{ \displaystyle \min_{g_k} L_{map}(g_k) = \sum_{i=1}^{m_k} \mid y_i^k - g_k(x_i^k)\mid^2 }[/math]. Back-propagation algorithm can be applied to solve this optimization problem.
Training of Deconfusing-Net: The task allocation is re-evaluated during the training phase while the parameters of the mapping-net remain fixed. To minimize the original risk, every sample [math]\displaystyle{ (x, y) }[/math] will be assigned to [math]\displaystyle{ g_k }[/math] that is closest to label y among all different [math]\displaystyle{ k }[/math]s. Mapping-net thus provides a temporary solution for deconfusing-net: [math]\displaystyle{ \hat{h}(x_i, y_i) = arg \displaystyle\min_{k} \mid y_i - g_k(x_i)\mid^2 }[/math]. The optimization becomes: [math]\displaystyle{ \displaystyle \min_{h} L_{dec}(h) = \sum_{i=1}^{m} \mid {h}(x_i, y_i) - \hat{h}(x_i, y_i)\mid^2 }[/math]. Similarly, the optimization problem can be solved by updating the deconfusing-net with a back-propagation algorithm.
The two optimization stages are carried out alternately until the solution converges.
Experiment
Setup
3 data sets are used to compare CSL to existing methods, 1 function regression task and 2 image classification tasks.
Function Regression: The function regression data comes in the form of [math]\displaystyle{ (x_i,y_i),i=1,...,m }[/math] pairs. However, unlike typical regression problems, there are multiple [math]\displaystyle{ f_j(x),j=1,...,n }[/math] mapping functions, so the goal is to recover both the mapping functions [math]\displaystyle{ f_j }[/math] as well as determine which mapping function corresponds to each of the [math]\displaystyle{ m }[/math] observations. 3 scalar-valued, scalar-input functions that intersect at several points with each other have been chosen as the different tasks.
Colorful-MNIST: The first image classification data set consists of the MNIST digit data that has been colored. Each observation in this modified set consists of a colored image ([math]\displaystyle{ x_i }[/math]) and either the color, or the digit it represents ([math]\displaystyle{ y_i }[/math]). The goal is to recover the classification task ("color" or "digit") for each observation and construct the 2 classifiers for both tasks.
Kaggle Fashion Product: This data set has more observations than the "colored-MNIST" data and consists of pictures labelled with either the “Gender”, “Category”, and “Color” of the clothing item.
Use of Pre-Trained CNN Feature Layers
In the Kaggle Fashion Product experiment, CSL trains fully-connected layers that have been attached to feature-identifying layers from pre-trained Convolutional Neural Networks.
Metrics of Confusing Supervised Learning
There are two measures of accuracy used to evaluate and compare CSL to other methods, corresponding respectively to the accuracy of the task labelling and the accuracy of the learned mapping function.
Task Prediction Accuracy: [math]\displaystyle{ \alpha_T(j) }[/math] is the average number of times the learned deconfusing function [math]\displaystyle{ h }[/math] agrees with the task-assignment ability of humans [math]\displaystyle{ \tilde h }[/math] on whether each observation in the data "is" or "is not" in task [math]\displaystyle{ j }[/math].
$$ \alpha_T(j) = \operatorname{max}_k\frac{1}{m}\sum_{i=1}^m I[h(x_i,y_i;f_k),\tilde h(x_i,y_i;f_j)]$$
The max over [math]\displaystyle{ k }[/math] is taken because we need to determine which learned task corresponds to which ground-truth task.
Label Prediction Accuracy: [math]\displaystyle{ \alpha_L(j) }[/math] again chooses [math]\displaystyle{ f_k }[/math], the learned mapping function that is closest to the ground-truth of task [math]\displaystyle{ j }[/math], and measures its average absolute accuracy compared to the ground-truth of task [math]\displaystyle{ j }[/math], [math]\displaystyle{ f_j }[/math], across all [math]\displaystyle{ m }[/math] observations.
$$ \alpha_L(j) = \operatorname{max}_k\frac{1}{m}\sum_{i=1}^m 1-\dfrac{|g_k(x_i)-f_j(x_i)|}{|f_j(x_i)|}$$
Results
Given confusing data, CSL performs better than traditional supervised learning methods, Pseudo-Label(Lee, 2013), and SMiLE(Tan et al., 2017). This is demonstrated by CSL's [math]\displaystyle{ \alpha_L }[/math] scores of around 95%, compared to [math]\displaystyle{ \alpha_L }[/math] scores of under 50% for the other methods. This supports the assertion that traditional methods only learn the means of all the ground-truth mapping functions when presented with confusing data.
Function Regression: In order to "correctly" partition the observations into the correct tasks, a 5-shot warm-up was used. In this situaion, the CSL methods work well learning the ground-truth. That means the initialization of the neural network is set up properly.
Image Classification: Visualizations created through Spectral embedding confirm the task labelling proficiency of the deconfusing neural network [math]\displaystyle{ h }[/math].
The classification and function prediction accuracy of CSL are comparable to supervised learning programs that have been given access to the ground-truth labels.
Application of Multi-label Learning
CSL also had better accuracy than traditional supervised learning methods, Pseudo-Label(Lee, 2013), and SMiLE(Tan et al., 2017) when presented with partially labelled multi-label data [math]\displaystyle{ (x_i,y_i) }[/math], where [math]\displaystyle{ y_i }[/math] is a [math]\displaystyle{ n }[/math]-long indicator vector for whether the image [math]\displaystyle{ (x_i,y_i) }[/math] corresponds to each of the [math]\displaystyle{ n }[/math] labels
Limitations
Number of Tasks: The number of tasks is determined by increasing the task numbers progressively and testing the performance. Ideally, a better way of deciding the number of tasks is expected rather than increasing it one by one and seeing which is the minimum number of tasks that gives the smallest risk. Adding low-quality constraints to deconfusing-net is a reasonable solution to this problem.
Learning of Basic Features: The CSL framework is not good at learning features. So far, a pre-trained CNN backbone is needed for complicated image classification problems. Even though the effectiveness of the proposed algorithm in learning confusing data based on pre-trained features hasn't been affected, the full-connect network can only be trained based on learned CNN features. It is still a challenge for the current algorithm to learn basic features directly through a CNN structure and understand tasks simultaneously.
Conclusion
This paper proposes the CSL method for tackling the multi-task learning problem with manual task annotations in the input data. The model obtains a basic task concept by differentiating multiple mappings. The paper also demonstrates that the CSL method is an important step to moving from Narrow AI towards General AI for multi-task learning.
However, there are some limitations that can be improved for future work: The repeated training process of determining the lowest best task number that has the closest to zero causes inefficiency in the learning process; The current algorithm is difficult to learn basic features directly through the CNN structure, and it is necessary to learn and train a fully connected network based on CNN features in the experiment.
Critique
The classification accuracy of CSL was made with algorithms not designed to deal with confusing data and which do not first classify the task of each observation.
Human task annotation is also imperfect, so one additional application of CSL may be to attempt to flag task annotation errors made by humans, such as in sorting comments for items sold by online retailers; concerned customers in particular may not correctly label their comments as "refund", "order didn't arrive", "order damaged", "how good the item is" etc.
This algorithm will also have a huge issue in scaling, as the proposed method requires repeated training processes, so it might be too expensive for researchers to implement and improve on this algorithm.
This research paper should have included a plot on loss (of both functions) against epochs in the paper. A common issue with fixing the parameters of one network and updating the other is the variability during training. This is prevalent in other algorithms with similar training methods such as generative adversarial networks (GAN). For instance, mode collapse is the issue of one network stuck in a local minima and other networks that rely on this network may receive incorrect signals during backpropagation. In the case of CSL-Net, since the Deconfusing-Net directly relies on Mapping-Net for training labels, if the Mapping-Net is unable to sufficiently converge, the Deconfusing-Net may incorrectly learn the mapping from inputs to task. For data with high noise, oscillations may severely prolong the time needed for converge because of the strong correlation in prediction between the two networks.
- It would be interesting to see this implemented in more examples, to test the robustness to different types of data.
Even though this paper has already included some examples when testing the CSL in experiments, it will be better to include more detailed examples for partial-label in the "Application of Multi-label Learning" section.
References
[1] Su, Xin, et al. "Task Understanding from Confusing Multi-task Data."
[2] Caruana, R. (1997) "Multi-task learning"
[3] Lee, D.-H. Pseudo-label: The simple and efficient semi-supervised learning method for deep neural networks. Workshop on challenges in representation learning, ICML, vol. 3, 2013, pp. 2–8.
[4] Tan, Q., Yu, Y., Yu, G., and Wang, J. Semi-supervised multi-label classification using incomplete label information. Neurocomputing, vol. 260, 2017, pp. 192–202.
[5] Chavdarova, Tatjana, and François Fleuret. "Sgan: An alternative training of generative adversarial networks." In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 9407-9415. 2018.