THE LOGICAL EXPRESSIVENESS OF GRAPH NEURAL NETWORKS
Presented By
Abhinav Jain
Background
The ability of graph neural networks (GNNs) for distinguishing nodes in graphs has been recently characterized in terms of the Weisfeiler-Lehman (WL) test for checking graph isomorphism. The WL test works by constructing labeling of the nodes of the graph, in an incremental fashion, and then decides whether two graphs are isomorphic by comparing the labeling of each graph. To state the connection between GNNs and this test, consider the simple GNN architecture that updates the feature vector of each graph node by combining it with the aggregation of the feature vectors of its neighbors. This characterization, however, does not settle the issue of which Boolean node classifiers (i.e., functions classifying nodes in graphs as true or false) can be expressed by GNNs.

The impacts of adversarial attacks can be life-threatening in the real world. Consider the case of driverless cars where the model installed in a car is trying to read a STOP sign on the road. However, if the STOP sign is replaced by an adversarial image of the original image, and if that new image is able to fool the model to not make a decision to stop, it can lead to an accident. Hence it becomes really important to design the classifiers such that these classifiers are immune to such adversarial attacks.
While training a deep network, the network is trained on a set of augmented images along with the original images. For any given image, there are multiple augmented images created and passed to the network to ensure that a model is able to learn from the augmented images as well. During the validation phase, after labeling an image, the defenses check whether there exists an image of a different label within a region of a certain unit radius of the input. Mathematically, such an adversarial example [math]\displaystyle{ x' }[/math] satisfies [math]\displaystyle{ distance(x,x')=\delta, f(x)\neq f(x') }[/math], where [math]\displaystyle{ \delta }[/math] is some small number and [math]\displaystyle{ f(\cdot) }[/math] is the image label. If the classifier assigns all images within the specified region ball the same class label, then a certificate is issued. This certificate ensures that the model is protected from adversarial attacks and is called Certified Defense. The image below shows a certified region (in red)
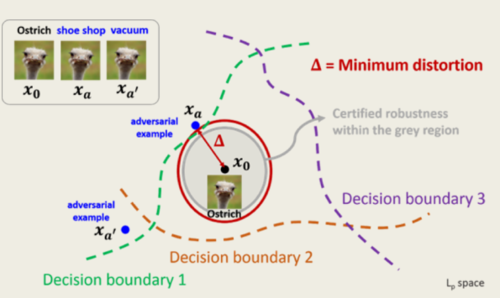
Introduction
Conventional deep learning models are generally highly sensitive to adversarial perturbations (Szegedy et al., 2013) in a way that natural-looking but minimally augmented images have been able to manipulate those models by causing misclassifications. While in the last few years, several defenses have been built that protect neural networks against such attacks (Madry et al., 2017; Shafahi et al., 2019), but these defenses are based on heuristics and tricks that are often easily breakable (Athalye et al. 2018). This has motivated a lot of researchers to work on certifiably secure networks — classifiers that produce a label for an inputted image in which the classification remains constant within a bounded set of perturbations around the original inputted image . Certified defenses have thus far considered [math]\displaystyle{ l_\text{p} }[/math]-bounded attacks where after labelling an input, if there does not exists an image resulting in a different label that is within the [math]\displaystyle{ l_\text{p} }[/math] norm ball of radius [math]\displaystyle{ \epsilon }[/math], centred at the original input, then a certificate is issued. Most of the certified defenses created so far focus on deflecting [math]\displaystyle{ l_\text{p} }[/math]-bounded attacks where [math]\displaystyle{ p }[/math] = 2 or infinity.
In this paper, the authors have demonstrated that a system that relies on certificates as a measure of label security can be exploited. The whole idea of the paper is to show that even though the system has a certified defense mechanism, it does not guarantee security against adversarial attacks. This is done by presenting a new class of adversarial examples that target not only the classifier output label but also the certificate. The first step is to add adversarial perturbations to images that are large in the [math]\displaystyle{ l_\text{p} }[/math]-norm (larger than the radius of the certificate region of the original image) and produce attack images that are outside the certificate boundary of the original image certificate and has images of the same (wrong) label. The result is a 'spoofed' certificate with a seemingly strong security guarantee despite being adversarially manipulated.
The following three conditions should be met while creating adversarial examples:
1. Imperceptibility: the adversarial image looks like the original example.
2. Misclassification: the certified classifier assigns an incorrect label to the adversarial example.
3. Strongly certified: the certified classifier provides a strong radius certificate for the adversarial example.
The main focus of the paper is to attack the certificate of the model. The authors argue that the model can be attacked, no matter how strong the certificate of the model is.
Approach
The approach used by the authors in this paper is 'Shadow Attack', which is a generalization of the well known Projected Gradient Descent (PGD) attack. PGD, a universal first order adversary [4], is the only method to greatly improve NN model robustness among all the defenses appearing in ICLR2018 and CVPR2018 [5]. The fundamental idea of the PGD attack is the same where a bunch of adversarial images are created in order to fool the network to make a wrong prediction. PGD attack solves the following optimization problem where [math]\displaystyle{ L }[/math] is the classification loss and the constraint corresponds to the minimal change done to the input image. For a recent review on adversarial attacks and more information of PGD attacks, see [1].
\begin{align} max_{\delta }L\left ( \theta, x + \delta \right ) \tag{1} \label{eq:op} \end{align}
\begin{align} s.t. \left \|\delta \right \|_{p} \leq \epsilon \end{align}
Shadow attack on the other hand targets the certificate of the defenses by creating a new 'spoofed' certificate outside the certificate region of the input image. Shadow attack solves the following optimization problem where [math]\displaystyle{ C }[/math], [math]\displaystyle{ TV }[/math], and [math]\displaystyle{ Dissim }[/math] are the regularizers.
\begin{align} max_{\delta} L\left (\theta ,x+\delta \right ) - \lambda_{c}C\left (\delta \right )-\lambda_{tv}TV\left ( \delta \right )-\lambda_{s}Dissim\left ( \delta \right ) \tag{2} \label{eq:op1} \end{align}
In equation \eqref{eq:op1}, [math]\displaystyle{ C }[/math] in the above equation corresponds to the color regularizer which makes sure that minimal changes are made to the color of the input image. [math]\displaystyle{ TV }[/math] corresponds to the Total Variation or smoothness parameter which makes sure that the smoothness of the newly created image is maintained. [math]\displaystyle{ Dissim }[/math] corresponds to the similarity parameter which makes sure that all the color channels (RGB) are changed equally.
The perturbations created in the original images are -
1. small
2. smooth
3. without dramatic color changes
There are two ways to ensure that this dissimilarity will not happen or will be very low and the authors have shown that both of these methods are effective.
- 1-channel attack: This strictly enforces [math]\displaystyle{ \delta_{R,i} \approx \delta_{G,i} \approx \delta_{B,i} \forall i }[/math] i.e. for each pixel, the perturbations of all channels are equal and there will be [math]\displaystyle{ \delta_{ W \times H} }[/math], where the size of the image is [math]\displaystyle{ 3 \times W \times H }[/math] as the preturbation. In this case, [math]\displaystyle{ Dissim(\delta)=0 }[/math].
- 3-channel attack: In this kind of attack, the perturbations in different channels of a pixel are not equal and it uses [math]\displaystyle{ \delta_{3 \times W \times H} }[/math] with the [math]\displaystyle{ Dissim(\delta) = || \delta_{R}- \delta_{B}||_p + || \delta_{G}- \delta_{B}||_p +|| \delta_{R}- \delta_{G}||_p }[/math] as the dissimilarity cost function.
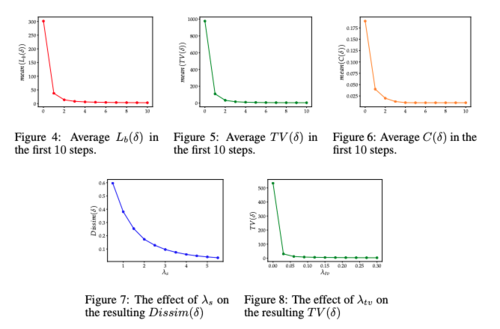
Ablation Study of the Attack parameters
In order to determine the required number of SGD steps, the effect of [math]\displaystyle{ \lambda_s }[/math], and the importance of [math]\displaystyle{ \lambda_s }[/math] on the each losses in the cost function, the authors have tried different values of these parameters using the first example from each class of the CIFAR-10 validation set. Based on figure 4, 5, and 6, we can see that the [math]\displaystyle{ L(\delta) }[/math] (classification loss), [math]\displaystyle{ TV(\delta) }[/math] (Total Variation loss), [math]\displaystyle{ C(\delta) }[/math] (color regularizer) will converge to zero with 10 SGD steps. Note that since only 1-channel attack was used in this part of the experiment the [math]\displaystyle{ dissim(\delta) }[/math]was indeed zero. In figure 6 and 7, we can see the effect of [math]\displaystyle{ \lambda_s }[/math] on the dissimilarity loss and the effect of [math]\displaystyle{ \lambda_{tv} }[/math] on the total variation loss respectively.
Experiments
The authors used two experiments to prove that their approach to attack a certified model was actually able to break those defenses. The datasets used for both of these experiments were CIFAR10 and ImageNet dataset.
Attack on Randomized Smoothing
Randomized Smoothing is an adversarial defense against [math]\displaystyle{ l_\text{p} }[/math]-norm bounded attacks. The deep neural network model is trained on a randomly augmented batch of images. Perturbations are made to the original image such that they satisfy the previously defined conditions and spoof certificates are generated for an incorrect class by generating multiple adversarial images.
The following table shows the results of applying the 'Shadow Attack' approach to Randomized Smoothing -
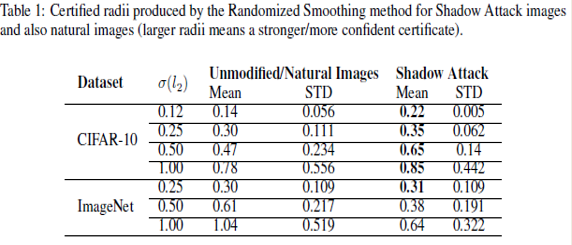
The third and the fifth column correspond to the mean radius of the certified region of the original image and the mean radius of the spoof certificate of the perturbed images, respectively. It was observed that the mean radius of the certificate of adversarial images was greater than the mean radius of the original image certificate. This proves that the 'Shadow Attack' approach was successful in creating spoof certificates of greater radius and with the wrong label. This also proves that the approach used in the paper was successful in breaking the certified defenses.
Attack on CROWN-IBP
Crown IBP is an adversarial defense against [math]\displaystyle{ l_\text{inf} }[/math]-norm bounded attacks. The same approach was applied for the CROWN-IBP defense and the table below shows the results.

The above table shows the robustness errors in the case of the CROWN-IBP method and the attack images. It is seen that the errors in the case of the attack were less than the equivalent errors for CROWN-IBP, which suggests that the authors' 'Shadow Attack' approach was successful in breaking the [math]\displaystyle{ l_\text{inf} }[/math]-norm certified defenses as well.
Conclusion
From the above approach used in a couple of experiments, we can conclude that it is possible to produce adversarial examples with ‘spoofed’ certified robustness by using large-norm perturbations. The perturbations generated are smooth and natural-looking while being large enough in norm to escape the certification regions of state-of-the-art principled defenses. The major takeaway of the paper would be that the certificates produced by certifiably robust classifiers are not always good indicators of robustness or accuracy.
Critiques
It is noticeable in this paper that using the mathematical formulation of the defenses and certifications is considered a weak method, whereas the constraint is imposed by [math]\displaystyle{ l_{p} }[/math] as assumed in equation \eqref{eq:op}. The top models can not achieve certifications beyond [math]\displaystyle{ \epsilon = 0.3 }[/math] disturbance in [math]\displaystyle{ l_{2} }[/math] norm, while disturbances [math]\displaystyle{ \epsilon = 4 }[/math] added to the target input are barely noticeable by human eyes, and [math]\displaystyle{ \epsilon = 100 }[/math] , when applied to the original image are still easily classified by humans as belonging to the same class. As discussed by many authors, the perception of multi-dimensional space by human eyes goes beyond what the [math]\displaystyle{ l_{p} }[/math] norm is capable of capturing and synthesizing. It is yet to be proposed more comprehensive metrics and algorithms capable of capturing the correlation between pixels of an image or input data which can better translate to optimization algorithms how humans distinguish features of an input image. Such a metric would allow the optimization algorithms to have better intuition on the subtle variations introduced by adversaries in the input data.
References
[1] Xu, H., Ma, Y., Liu, H. C., Deb, D., Liu, H., Tang, J. L., & Jain, A. K. (2020). Adversarial Attacks and Defenses in Images, Graphs and Text: A Review. International Journal of Automation and Computing, 17(2), 151–178.
[2] Christian Szegedy,Wojciech Zaremba, Ilya Sutskever, Joan Bruna, Dumitru Erhan, Ian Goodfellow, and Rob Fergus. Intriguing properties of neural networks. arXiv preprint arXiv:1312.6199, 2013.
[3] Ali Shafahi, Mahyar Najibi, Amin Ghiasi, Zheng Xu, John Dickerson, Christoph Studer, Larry S Davis, Gavin Taylor, and Tom Goldstein. Adversarial training for free! arXiv preprint arXiv:1904.12843, 2019.
[4] Aleksander Madry, Aleksandar Makelov, Ludwig Schmidt, Dimitris Tsipras, and Adrian Vladu. Towards deep learning models resistant to adversarial attacks. arXiv preprint arXiv:1706.06083, 2017.
[5] Anish Athalye, Nicholas Carlini, and David Wagner. Obfuscated gradients give a false sense of security: Circumventing defenses to adversarial examples. arXiv preprint arXiv:1802.00420, 2018.