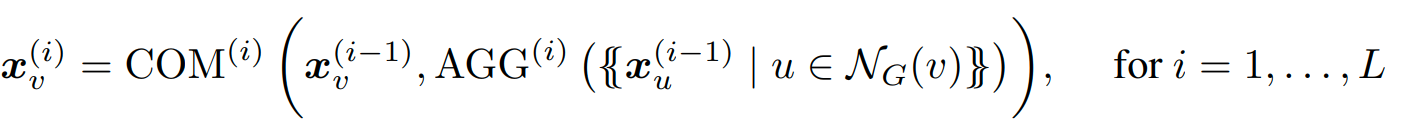THE LOGICAL EXPRESSIVENESS OF GRAPH NEURAL NETWORKS: Difference between revisions
No edit summary |
No edit summary |
||
| Line 48: | Line 48: | ||
According to their theorem, A logical classifier is captured by AC-GNNs if and only if it can be expressed in graded modal logic. This holds no matter which aggregate and combine operators are considered, i.e., this is a limitation of the architecture for AC-GNNs, not of the specific functions that one chooses to update the features. | According to their theorem, A logical classifier is captured by AC-GNNs if and only if it can be expressed in graded modal logic. This holds no matter which aggregate and combine operators are considered, i.e., this is a limitation of the architecture for AC-GNNs, not of the specific functions that one chooses to update the features. | ||
== Concepts == | |||
The main shortcoming of AC-GNNs for expressing such classifiers is their local behavior. A natural way to break such a behavior is to allow for a global feature computation on each layer of the GNN. This is called a global attribute computation in the framework of Battaglia et al. (2018). Following the recent GNN literature (Gilmer et al., 2017; Morris et al., 2019; Xu et al., 2019), we refer to this global operation as a readout. Formally, an aggregate-combine-readout GNN (ACR-GNN) extends AC-GNNs by specifying readout functions READ(i), which aggregate the current feature vectors of all the nodes in a graph. | |||
Then, the vector <math>{x_v}^i</math> of each node v in G on each layer i, is computed by the following formula: | |||
[[File:a227-formula-final]] | |||
[[File: | |||
== Experiments == | == Experiments == | ||
Revision as of 13:32, 21 November 2020
Presented By
Abhinav Jain
Background
Graph neural networks (GNNs) (Merkwirth & Lengauer, 2005; Scarselli et al., 2009) are a class of neural network architectures that have recently become popular for a wide range of applications dealing with structured data, e.g., molecule classification, knowledge graph completion, and Web page ranking (Battaglia et al., 2018; Gilmer et al., 2017; Kipf & Welling, 2017; Schlichtkrull et al., 2018). The main idea behind GNNs is that the connections between neurons are not arbitrary but reflect the structure of the input data. This approach is motivated by convolutional and recurrent neural networks and generalizes both of them (Battaglia et al., 2018). Despite the fact that GNNs have recently been proven very efficient in many applications, their theoretical properties are not yet well-understood.
The ability of graph neural networks (GNNs) for distinguishing nodes in graphs has been recently characterized in terms of the Weisfeiler-Lehman (WL) test for checking graph isomorphism. The WL test works by constructing labeling of the nodes of the graph, in an incremental fashion, and then decides whether two graphs are isomorphic by comparing the labeling of each graph. This characterization, however, does not settle the issue of which Boolean node classifiers (i.e., functions classifying nodes in graphs as true or false) can be expressed by GNNs. To state the connection between GNNs and this test, consider the simple GNN architecture that updates the feature vector of each graph node by combining it with the aggregation of the feature vectors of its neighbors. We call such GNNs aggregate-combine GNNs, or AC-GNNs. Moreover, there are AC-GNNs that can reproduce the WL labeling. This does not imply, however, that AC-GNNs can capture every node classifier—that is, a function assigning true or false to every node—that is refined by the WL test. The author's work aims to answer the question of what are the node classifiers that can be captured by GNN architectures such as AC-GNNs.
Introduction
They tackle this problem by focusing on Boolean classifiers expressible as formulas in the logic FOC2, a well-studied fragment of first-order logic. FOC2 is tightly related to the WL test, and hence to GNNs. They start by studying a popular class of GNNs, which they call AC-GNNs, in which the features of each node in the graph are updated, in successive layers, only in terms of the features of its neighbors.
Given the connection between AC-GNNs and WL on the one hand, and that between WL and FOC2 on the other hand, one may be tempted to think that the expressivity of AC-GNNs coincides with that of FOC2. However, the reality is not as simple, and there are many FOC2 node classifiers (e.g., the trivial one above) that cannot be expressed by AC-GNNs. This leaves us with the following natural questions. First, what is the largest fragment of FOC2 classifiers that can be captured by AC-GNNs? Second, is there an extension of AC-GNNs that allows expressing all FOC2 classifiers? In this paper, they provide answers to these two questions.
The following are the main contributions:
1. They characterize exactly the fragment of FOC2 formulas that can be expressed as ACGNNs. This fragment corresponds to graded modal logic (de Rijke, 2000), or, equivalently, to the description logic ALCQ, which has received considerable attention in the knowledge representation community (Baader et al., 2003; Baader & Lutz, 2007).
2. Next, they extend the AC-GNN architecture in a very simple way by allowing global readouts, wherein each layer they also compute a feature vector for the whole graph and combine it with local aggregations; they call these aggregate-combine-readout GNNs (ACR-GNNs). These networks are a special case of the ones proposed by Battaglia et al. (2018) for relational reasoning over graph representations. In this setting, they prove that each FOC2 formula can be captured by an ACR-GNN.
They experimentally validate our findings showing that the theoretical expressiveness of ACR-GNNs, as well as the differences between AC-GNNs and ACR-GNNs, can be observed when they learn from examples. In particular, they show that on synthetic graph data conforming to FOC2 formulas, ACGNNs struggle to fit the training data while ACR-GNNs can generalize even to graphs of sizes not seen during training.
Architecture
We concentrate on the problem of Boolean node classification: given a (simple, undirected) graph G = (V, E) in which each vertex v ∈ V has an associated feature vector xv, we wish to classify each graph node as true or false; in this paper, we assume that these feature vectors are one-hot encodings of node colors in the graph, from a finite set of colors. The neighborhood NG(v) of a node v ∈ V is the set {u | {v, u} ∈ E}. The basic architecture for GNNs, and the one studied in recent studies on GNN expressibility (Morris et al., 2019; Xu et al., 2019), consists of a sequence of layers that combine the feature vectors of every node with the multiset of feature vectors of its neighbors. Formally, let AGG and COM be two sets of aggregation and combination functions. An aggregate-combine GNN (AC-GNN) computes vectors [math]\displaystyle{ {x_v}^i }[/math] for every node v of the graph G, via the recursive formula
where each [math]\displaystyle{ {x_v}^0 }[/math] is the initial feature vector [math]\displaystyle{ {x_v} }[/math] of v. Finally, each node v of G is classified according to a Boolean classification function CLS applied to [math]\displaystyle{ {x_v}^{(L)} }[/math]
Concepts
1. LOGICAL NODE CLASSIFIER Their study relates the power of GNNs to that of classifiers expressed in first-order (FO) predicate logic over (undirected) graphs where each vertex has a unique color (recall that we call these classifiers logical classifiers).
2. LOGIC FOC2 The logic FOC2 allows for formulas using all FO constructs and counting quantifiers, but restricted to only two variables. Note that, in terms of their logical expressiveness, we have that FOC2 is strictly less expressive than FO (as counting quantifiers can always be mimicked in FO by using more variables and disequalities), but is strictly more expressive than FO2, the fragment of FO that allows formulas to use only two variables (as β(x) belongs to FOC2 but not to FO2).
3. FOC2 AND AC-GNN CLASSIFIER While it is true that two nodes are declared indistinguishable by the WL test if and only if they are indistinguishable by all FOC2 classifiers (Proposition 3.2), and if the former holds then such nodes cannot be distinguished by AC-GNNs (Proposition 2.1), this by no means tells us that every FOC2 classifier can be expressed as an AC-GNN. The answer to this problem is covered in the next section.
THE EXPRESSIVE POWER OF AC-GNNS
AC-GNNs capture any FOC2 classifier as long as we further restrict the formulas so that they satisfy such a locality property. This happens to be a well-known restriction of FOC2, and corresponds to graded modal logic (de Rijke, 2000), which is fundamental for knowledge representation. The idea of graded modal logic is to force all subformulas to be guarded by the edge predicate E. This means that one cannot express in graded modal logic arbitrary formulas of the form ∃yϕ(y), i.e., whether there is some node that satisfies property ϕ. Instead, one is allowed to check whether some neighbor y of the node x where the formula is being evaluated satisfies ϕ. That is, we are allowed to express the formula ∃y (E(x, y) ∧ ϕ(y)) in the logic as in this case ϕ(y) is guarded by E(x, y).
The relationship between AC-GNNs and graded modal logic goes further: we can show that graded modal logic is the “largest” class of logical classifiers captured by AC-GNNs. This means that the only FO formulas that AC-GNNs are able to learn accurately are those in graded modal logic.
According to their theorem, A logical classifier is captured by AC-GNNs if and only if it can be expressed in graded modal logic. This holds no matter which aggregate and combine operators are considered, i.e., this is a limitation of the architecture for AC-GNNs, not of the specific functions that one chooses to update the features.
Concepts
The main shortcoming of AC-GNNs for expressing such classifiers is their local behavior. A natural way to break such a behavior is to allow for a global feature computation on each layer of the GNN. This is called a global attribute computation in the framework of Battaglia et al. (2018). Following the recent GNN literature (Gilmer et al., 2017; Morris et al., 2019; Xu et al., 2019), we refer to this global operation as a readout. Formally, an aggregate-combine-readout GNN (ACR-GNN) extends AC-GNNs by specifying readout functions READ(i), which aggregate the current feature vectors of all the nodes in a graph. Then, the vector [math]\displaystyle{ {x_v}^i }[/math] of each node v in G on each layer i, is computed by the following formula:
Experiments
The authors used two experiments to prove that their approach to attack a certified model was actually able to break those defenses. The datasets used for both of these experiments were CIFAR10 and ImageNet dataset.
Attack on Randomized Smoothing
Randomized Smoothing is an adversarial defense against [math]\displaystyle{ l_\text{p} }[/math]-norm bounded attacks. The deep neural network model is trained on a randomly augmented batch of images. Perturbations are made to the original image such that they satisfy the previously defined conditions and spoof certificates are generated for an incorrect class by generating multiple adversarial images.
The following table shows the results of applying the 'Shadow Attack' approach to Randomized Smoothing -
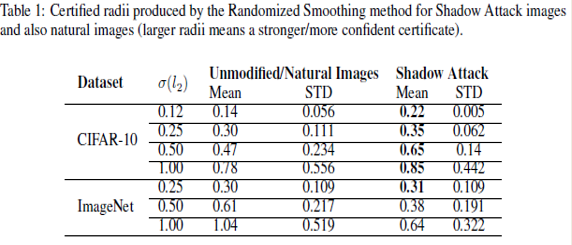
The third and the fifth column correspond to the mean radius of the certified region of the original image and the mean radius of the spoof certificate of the perturbed images, respectively. It was observed that the mean radius of the certificate of adversarial images was greater than the mean radius of the original image certificate. This proves that the 'Shadow Attack' approach was successful in creating spoof certificates of greater radius and with the wrong label. This also proves that the approach used in the paper was successful in breaking the certified defenses.
Attack on CROWN-IBP
Crown IBP is an adversarial defense against [math]\displaystyle{ l_\text{inf} }[/math]-norm bounded attacks. The same approach was applied for the CROWN-IBP defense and the table below shows the results.

The above table shows the robustness errors in the case of the CROWN-IBP method and the attack images. It is seen that the errors in the case of the attack were less than the equivalent errors for CROWN-IBP, which suggests that the authors' 'Shadow Attack' approach was successful in breaking the [math]\displaystyle{ l_\text{inf} }[/math]-norm certified defenses as well.
Conclusion
From the above approach used in a couple of experiments, we can conclude that it is possible to produce adversarial examples with ‘spoofed’ certified robustness by using large-norm perturbations. The perturbations generated are smooth and natural-looking while being large enough in norm to escape the certification regions of state-of-the-art principled defenses. The major takeaway of the paper would be that the certificates produced by certifiably robust classifiers are not always good indicators of robustness or accuracy.
Critiques
It is noticeable in this paper that using the mathematical formulation of the defenses and certifications is considered a weak method, whereas the constraint is imposed by [math]\displaystyle{ l_{p} }[/math] as assumed in equation \eqref{eq:op}. The top models can not achieve certifications beyond [math]\displaystyle{ \epsilon = 0.3 }[/math] disturbance in [math]\displaystyle{ l_{2} }[/math] norm, while disturbances [math]\displaystyle{ \epsilon = 4 }[/math] added to the target input are barely noticeable by human eyes, and [math]\displaystyle{ \epsilon = 100 }[/math] , when applied to the original image are still easily classified by humans as belonging to the same class. As discussed by many authors, the perception of multi-dimensional space by human eyes goes beyond what the [math]\displaystyle{ l_{p} }[/math] norm is capable of capturing and synthesizing. It is yet to be proposed more comprehensive metrics and algorithms capable of capturing the correlation between pixels of an image or input data which can better translate to optimization algorithms how humans distinguish features of an input image. Such a metric would allow the optimization algorithms to have better intuition on the subtle variations introduced by adversaries in the input data.
References
[1] Xu, H., Ma, Y., Liu, H. C., Deb, D., Liu, H., Tang, J. L., & Jain, A. K. (2020). Adversarial Attacks and Defenses in Images, Graphs and Text: A Review. International Journal of Automation and Computing, 17(2), 151–178.
[2] Christian Szegedy,Wojciech Zaremba, Ilya Sutskever, Joan Bruna, Dumitru Erhan, Ian Goodfellow, and Rob Fergus. Intriguing properties of neural networks. arXiv preprint arXiv:1312.6199, 2013.
[3] Ali Shafahi, Mahyar Najibi, Amin Ghiasi, Zheng Xu, John Dickerson, Christoph Studer, Larry S Davis, Gavin Taylor, and Tom Goldstein. Adversarial training for free! arXiv preprint arXiv:1904.12843, 2019.
[4] Aleksander Madry, Aleksandar Makelov, Ludwig Schmidt, Dimitris Tsipras, and Adrian Vladu. Towards deep learning models resistant to adversarial attacks. arXiv preprint arXiv:1706.06083, 2017.
[5] Anish Athalye, Nicholas Carlini, and David Wagner. Obfuscated gradients give a false sense of security: Circumventing defenses to adversarial examples. arXiv preprint arXiv:1802.00420, 2018.