Superhuman AI for Multiplayer Poker: Difference between revisions
| Line 24: | Line 24: | ||
Consider the Lemonade Stand example from Figure 1 Below. We have 4 players and the goal for each player is to find a spot in the ring that is furthest away from every other player. This way, each lemonade stand can cover as much selling region as possible and generate maximum revenue. In the left circle, we have three different Nash equilibria distinguished by different colours which would benefit everyone. The right circle is an illustration of what would happen if each player decides to calculate their own Nash equilibrium. | Consider the Lemonade Stand example from Figure 1 Below. We have 4 players and the goal for each player is to find a spot in the ring that is furthest away from every other player. This way, each lemonade stand can cover as much selling region as possible and generate maximum revenue. In the left circle, we have three different Nash equilibria distinguished by different colours which would benefit everyone. The right circle is an illustration of what would happen if each player decides to calculate their own Nash equilibrium. | ||
[[File:Lemonade_Example.png |center ]] | [[File:Lemonade_Example.png| 200px |center ]] | ||
<div align="center">Figure 1: Lemonade Stand Example</div> | <div align="center">Figure 1: Lemonade Stand Example</div> | ||
Revision as of 19:09, 17 November 2020
Presented by
Hansa Halim, Sanjana Rajendra Naik, Samka Marfua, Shawrupa Proshasty
Introduction
In the past two decades, most of the superhuman AI that were built can only beat human players in two-player zero-sum games. The most common strategy that the AI use to beat those games is to find the most optimal Nash equilibrium. A Nash equilibrium is the best possible choice that a player can take, regardless of what their opponent is going to choose.
More specifically, in the game of poker we only have AI models that can beat human players in two-player settings. Poker is a great challenge in AI and game theory because it captures the challenges in hidden information so elegantly. This means that developing a superhuman AI in multiplayer poker is the remaining great milestone in this field, because there is no polynomial-time algorithm that can find a Nash equilibrium in two-player non-zero-sum games, and having one would have surprising implications in computational complexity theory.
In this paper, the AI whom we call Pluribus, is capable of defeating human professional poker players in Texas hold'em poker which is a six-player poker game and is the most commonly played format in the world. The algorithm that is used are not guaranteed to converge to a Nash algorithm outside of two-player zero-sum games. However, it has uses a strong strategy that is capable of consistently defeating elite human professionals. Which shows that despite not having strong theoretical guarantees on performance, they are capable of applying a wider class of superhuman strategies.
Challenges of Multiplayer Games
Many AI have reached superhuman performance in games like checkers, chess, two-player limit poker, Go, and two-player no-limit poker. Nash equilibrium has been proven to always exists in all finite games, and the challenge is to find the equilibrium. It is the best possible strategy and is unbeatable in two-player zero-sum games, since it guarantees to not lose in expectation regardless what the opponent is doing.
The insufficiency with current AI systems is that they only try to achieve Nash equilibriums instead of trying to actively detect and exploit weaknesses in opponents. For example, let's consider the game of Rock-Paper-Scissors, the Nash equilibrium is to randomly pick any option with equal probability. However, we can see that this means the best strategy that the opponent can have will result in a tie. Therefore, in this example our player cannot win in expectation.
Now let's try to combine the Nash equilibrium strategy and opponent exploitation. We can initially use the Nash equilibrium strategy and then change our strategy over time to exploit the observed weaknesses of our opponent. For example, we switch to always play Rock against our opponent who always plays Scissors. However, by shifting away from the Nash equilibrium strategy, it opens up the possibility for our opponent to use our strategy against ourselves. For example, they notice we always play Rock and thus they will now always play Paper.
Trying to approximate a Nash equilibrium is hard in theory, and in games with more than two players, it can only find a handful of possible strategies per player. Currently existing techniques to find ways to exploit an opponent require way too many samples and is not competitive enough outside of small games.
Finding a Nash equilibrium in three or more players is a problem itself. If we can efficiently compute a Nash equilibrium in games more than two players, it is highly questionable if playing the Nash equilibrium strategy is a good choice. Additionally, if each player tries to find their own version of a Nash equilibrium, we could have infinitely many strategies and each player’s version of the equilibrium might not even be a Nash equilibrium.
Consider the Lemonade Stand example from Figure 1 Below. We have 4 players and the goal for each player is to find a spot in the ring that is furthest away from every other player. This way, each lemonade stand can cover as much selling region as possible and generate maximum revenue. In the left circle, we have three different Nash equilibria distinguished by different colours which would benefit everyone. The right circle is an illustration of what would happen if each player decides to calculate their own Nash equilibrium.
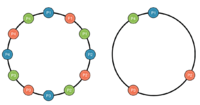
From the right circle in Figure 1, we can see that when each player tries to calculate their own Nash equilibrium, their own version of the equilibrium might not be a Nash equilibrium and thus they are not choosing the best possible location.
This shows that attempting to find a Nash equilibrium is not the best strategy outside of two-player zero-sum games, and our goal should not be focused on finding a specific game-theoretic solution. Instead, we need to focus on observations and empirical results that consistently defeat human opponents.
Theoretical Analysis
The core of Pluribus’s strategy was computed through self-play, in which the AI plays against copies of itself, without any data of human or prior AI play used as input. The AI player randomly and then gradually improves itself and its strategy. This self-play produces a strategy for the entire game offline, which we refer to as the blueprint strategy. During actual play against opponents, Pluribus improves upon the blueprint strategy by searching in real-time for the situations in which it finds itself during the game.
Pluribus uses forms of abstraction to make computations scalable. There are far too many decision points (a decision point in the game is a point where the player chooses to call, fold or check) in no-limit Texas hold 'em poker, so to reduce the complexity of the game, we eliminate some actions from consideration and also bucket similar decision points together in a process called abstraction. After abstraction, the bucketed decision points are treated as identical.
We use two kinds of abstraction in Pluribus: action abstraction and information abstraction. Action abstraction reduces the number of different actions the AI needs to consider. Pluribus only considers a few different bet sizes at any step. The exact number of bets it considers varies between 1 and 14 depending on the situation. The other form of abstraction that we use is information abstraction which drastically reduces the complexity of the game. Here, decision points that are similar in terms of what information has been revealed(in poker, the player’s cards and revealed board cards) are bucketed together. Therefore, during actual play against humans, Pluribus uses information abstraction only to reason about situations on future betting rounds, never the betting round that it is actually in. So information abstraction is also applied during offline self-play.
Blueprint Strategy and CFR
The blueprint strategy is computed using Monte Carlo Counterfactual Regret Minimization (MCCFR). CFR is commonly used in imperfect information games AI, where it is trained by repeatedly playing against itself, where it gradually improves by beating earlier versions of itself. Poker is best represented by a game tree structure which is computationally favorable and a game tree is represented as a tree structure where each node represents either a player’s decision, a chance event, or a terminal outcome and edges represent actions taken.
[PICTURE OF GAME TREE]
At the start of each iteration MCCFR stimulates a hand of poker randomly (Cards held by player at a given time) and designates one player as the traverser of the game tree. Once that is completed, the AI reviews the decision made by the traverser at a decision point in the game and investigates whether the decision was valuable by comparing it with other actions available to the traverser at that point and by also by investigating and comparing it with the future hypothetical decisions that would have been made following the other available actions. Counterfactual Regret factor is used to asses a decision, which is the difference between what the traverser would have received for choosing an action and what the traverser in expectation actually received on the iteration. The value of counter factual regret for a decision is updated over the iterations as more scenarios or decision points are encountered.
[Regret factor equation]
Thus regret is a numeric value, where a positive regret indicates you regret your decision, a negative regret indicates you are happy with decision and zero regret indicates that you are indifferent. At the end of each iteration, the traverser’s strategy is updated so actions with higher counterfactual regret is chosen with higher probability. CFR minimizes regret over many iterations until the average strategy over all iterations converges and the average strategy is the approximated Nash equilibrium. CFR guarantees in all finite games that all counterfactual regrets grow sublinearly in the number of iterations and so it assigns a weight of T to regret contributions at iteration T.
Pluribus uses this blueprint strategy in the first betting round when the number of decision points is small enough. Into the future of the game, in the subgames instead of assuming that all players play according to a single strategy, pluribus considers that each player may choose between k different strategies specialized to each player, when a leaf node is reached. This results in the searcher finding a strategy that is more balanced because choosing an unbalanced strategy(e.g., always playing Rock in Rock-Paper-Scissors) would be punished by an opponent shifting to one of the other continuation strategies (e.g playing paper).
Experimental Results
To test how well Pluribus functions, it was tested against human players in 2 formats. The first format included 5 human players and one copy of Pluribus (5H+1AI). The 13 human participants were poker players who have won more than $1M playing professionally and were provided with cash incentives to play their best. 10,000 hands of poker were played over 12 days with the 5H+1AI format by anonymizing the players by providing each of them with aliases that remained consistent throughout all their games. The aliases helped the players keep track of the tendencies and types of games played by each player over the 10,000 hands played.
The second format included one human player and 5 copies of Pluribus (1H+5AI) . There were 2 more professional players who split another 10,000 hands of poker by playing 5000 hands each and followed the same aliasing process as the first format. Performance was measured using milli big blinds per game, mbb/game, (i.e. the initial amount of money the second player has to put in the pot) which is the standard measure in the AI field. Additionally, AIVAT was used as the variance reduction technique to control for luck in the games, and significance tests were run at a 95% significance level with one-tailed t-tests as a check for Pluribus’s performance in being profitable.
Applying AIVAT it was found that for the first format, Pluribus won 48 mbb/game on average with standard error 25 mbb/game. This far exceeds the expected win-rate for 6-player Texas hold’em poker. The p-value of Pluribus being profitable in this format was 0.028. With the second format, Pluribus won 32 mbb/game on average with a standard error of 15 mbb/game and was determined as profitable with a p-value of 0.014.
As Pluribus’s strategy was not developed with any human data and was trained by self-play only, it is an unbiased and different perspective on how optimal play can be attained. A standard convention of “limping” in poker is confirmed to be not optimal by Pluribus since it initially experimented with it but eliminated this from its strategy over its games of self-play. On the other hand, another convention of “donk betting” that is dismissed by players was adopted by Pluribus much more often than played by humans, and is proven to be profitable.
Discussion
Lorem Ipsum Bla bla bla
Conclusion
Lorem Ipsum Bla bla bla
Critiques
Lorem Ipsum Bla bla bla
References
[1] Lorem Ipsum Bla bla bla [2] Lorem Ipsum Bla bla bla