Summary of A Probabilistic Approach to Neural Network Pruning: Difference between revisions
m (→Future Works) |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 144: | Line 144: | ||
As previously stated we will not provide a full characterization of the proof. Instead, we clarify why the authors made the three assumptions that appear in the theorem. | As previously stated we will not provide a full characterization of the proof. Instead, we clarify why the authors made the three assumptions that appear in the theorem. | ||
First, we comment on the Lipschitz continuity of <math display="inline">\sigma_{k}</math>. For our purposes function <math display="inline">g:\mathbb{R}^{n}\rightarrow\mathbb{R}^{n}</math> is Lipschitz continuous iff <math display="block">||g(x)-g(y)||_{2}\leq K||x-y||_{2}</math> for any <math display="inline">x,y\in\mathbb{R}^{n}</math> (see [ | First, we comment on the Lipschitz continuity of <math display="inline">\sigma_{k}</math>. For our purposes function <math display="inline">g:\mathbb{R}^{n}\rightarrow\mathbb{R}^{n}</math> is Lipschitz continuous iff <math display="block">||g(x)-g(y)||_{2}\leq K||x-y||_{2}</math> for any <math display="inline">x,y\in\mathbb{R}^{n}</math> (see [20] for more details on Lipschitz continuity). The intuition when <math display="inline">g:\mathbb{R}\rightarrow\mathbb{R}</math> is that <math display="inline">g</math> is Lipschitz just when its value never changes quicker than the function <math display="inline">h(x)=Kx</math>. The reason the activation functions are Lipschitz continuous is just because the proof of the main theorem relies on random matrix theory and, in particular, the probability that the 2-norms of random matrices exceed certain bounds. By ensuring that <math display="block">||\sigma(z_{l}^{*})-\sigma(z_{l})||_{2}\leq K_{l}||W_{l}^{*}x_{l}-W_{l}x_{l}||_{2}</math> the authors are able to extend the results of bounding the difference between vectors under random matrices, to bounding the difference between vectors under non-linear transformations (see section 4 of [18]). So, the results of random matrix theory can be harnessed to prove the main results. | ||
The second assumption is largely used to provide tighter bounds on the probabilities given in the relevant theorem. As such its role is mostly related to technical details (again see section 4 of [18]). | The second assumption is largely used to provide tighter bounds on the probabilities given in the relevant theorem. As such its role is mostly related to technical details (again see section 4 of [18]). | ||
| Line 156: | Line 156: | ||
==Future Works== | ==Future Works== | ||
Issues raised by | Issues raised by Blalock et al argue that in general, the community surrounding neural network pruning research suffers from a lack of standardization. Definitions tend to be ambiguous and comparisons are difficult to make between performances of different pruning algorithms. Overall, this sector will see much more research and focus in the near future. This paper is a foundation for theoretical works regarding pruning both FCNs and CNNs. Importantly, since nearly all network architectures can be replaced by some combination of FCNs and CNNs, this paper has application in pruning many different architectures. Applying these results to past works by Frankle & Carbin in 2018 gives a method to determine an upper bound on the number of weights available for pruning in a given layer in order to maintain the desired error margin. | ||
The paper’s analysis assumes that weights in the original network are independent. This assumption is not ideal, especially in CNNs. While the paper’s appendix discusses ways around it, no solution could be found. The authors suggest that an in-depth study of this assumption is warranted in the future. Another topic not explored fully is using gradients of the weights in the original network to determine more optimal pruning algorithms. | The paper’s analysis assumes that weights in the original network are independent. This assumption is not ideal, especially in CNNs. While the paper’s appendix discusses ways around it, no solution could be found. The authors suggest that an in-depth study of this assumption is warranted in the future. Another topic not explored fully is using gradients of the weights in the original network to determine more optimal pruning algorithms. | ||
Latest revision as of 00:30, 23 November 2021
Presented by
Stefan Vladusic, Waqas Hamed, Justin D'Astous, Ethan O'Farrell
Background
High performance neural networks often have a very large number of training parameters. Frankle and Carbin [2] propose the Lottery Ticket Hypothesis that a trained neural network will contain many smaller subnetworks containing the most important logic. When training these subnetworks in isolation after the initialization, they can acheive similar accuracy compared to the original network. Ramanujan et al [10] further proposes that the subnetworks can achieve similar accuracy without having to be further trained. However, finding these lottery tickets inside a large neural network is computationally expensive (NP hard in general).
There has been little research on the theoretical guarantees of pruning. This study, A Probabilistic Approach to Neural Network Pruning by Xin Qian and Diego Klabjan [18], focuses on the theoretical results from creating subnetworks by pruning weights. It covers pruning random weights in Fully Connected Networks (FCNs) and Convolutional Neural Networks (CNNs) as well as pruning weights based on their magnitude in FCNs. It does not cover the theoretical implications of pruning entire neurons.
Literature Review
Empirical Network Pruning: The theory on neural network pruning has transitioned from pruning individual connections based on the loss function [5] to pruning connections based on its magnitude [3]. Papers began to focus on pruning entire neurons [4] or convolution channels [6that could be redundant. Recently, the focus has shifted to instead find a smaller subnetwork inside an overparameterized network with comparable predictive power and prune the rest.
Theoretical Study of Network Pruning: Some research has looked into pruning FCNs with ReLU activation. Their work used the idea that a single ReLU neuron can be approximated using a two-hidden-layer neural network with constant width [8][9]. Other methods of pruning currently being researched are a greedy optimization based pruning method [11] and sampling-based pruning algorithms based on sensitivity scores [1][7].
Pruning
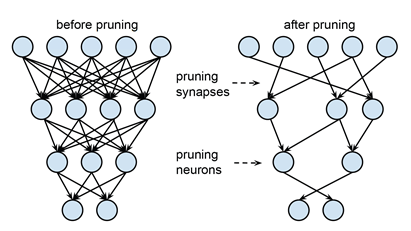
Deep neural networks can become computationally intensive and memory intensive. To tackle that people have employed neural network pruning in recent years. Pruning is simply the act of reducing the weights of a neural network layer. As explained in detail later, pruning can reduce the complexity of the network while keeping the difference in errors of the original neural network and the pruned neural network minimal. Pruning is either performed on individual weights or on entire neurons (whole column in a weight matrix). In the paper, only pruning individual weights has been discussed.
Pruning is a 3-step process that can be summarized as:
- Train the network.
- Prune the network.
- Re-train the network.
The figure [3] below demonstrates both pruning individual weights/synapses and pruning neurons.
Magnitude based pruning refers to reducing the number of weights in a layer based on the weight’s absolute value. The intuition behind this is that the weights with values close to zero, do not contribute significantly to the predictive ability of the network. To perform this, a mask matrix M, which has the same size as the weight matrix, is used. M has all entries equal to 1, except elements corresponding to weights to be pruned where the entry is instead 0. These weights are selected based on their magnitude. In the pruned network, the mask is multiplied element-wise with the weight matrix before re-training.
Random pruning also uses a mask matrix M. The weights to be pruned are decided randomly selected.
Pruning Fully Connected Networks
A Brief Comment on Our Review
The paper we are reviewing relies on proofs that are both technical and lengthy. The authors use 9 lemmas spanning order statistics, random matrix theory and probability theory in order to prove the main results. Furthermore, the authors provide 4 pruning techniques (with corresponding proofs). However these proofs are all quite similar. Consequently, we will not present the technical details of the proof, since we feel this would be too long and too complicated for a (relatively) short review. Instead, we hope to:
- Clarify the terminology used by the authors.
- Explain how this terminology intuitively describes pruning technique.
- Explain why the assumptions made in the magnitude based pruning technique are required.
- Briefly comment on the validity of these assumptions.
Clarifying the Objects of Study
In [18] the authors define the following standard objects and notation:
- [math]\displaystyle{ L+1 }[/math] denotes the depth the neural network (alternatively there are [math]\displaystyle{ L }[/math] hidden layers), with [math]\displaystyle{ l\in\{1,...,L\} }[/math] indexing hidden layers (the input layer is denoted with [math]\displaystyle{ l=0 }[/math]).
- [math]\displaystyle{ d_{l} }[/math] denotes the number of nodes in the hidden layer [math]\displaystyle{ l\in\{1,...,L\} }[/math].
- Let [math]\displaystyle{ v\in\mathbb{R}^{d_{l}} }[/math]. The [math]\displaystyle{ L_{0} }[/math] norm of [math]\displaystyle{ v }[/math] is denoted [math]\displaystyle{ ||v||_{0} }[/math], and specifies the number of non-zero entries in [math]\displaystyle{ v }[/math]. The [math]\displaystyle{ L_{2} }[/math] norm of [math]\displaystyle{ v }[/math] is denotes [math]\displaystyle{ ||v||_{2} }[/math], which denotes the Euclidean “standard” norm [math]\displaystyle{ ||v||_{2}=\sqrt{v^{T}v} }[/math].
- Let [math]\displaystyle{ A\in\mathbb{R}^{m\times n} }[/math] . The vectorization of [math]\displaystyle{ A }[/math] is defined as follows: [math]\displaystyle{ \text{vec}(A)=\left[A_{1,1},...,A_{1,n},...,A_{m,1},...,A_{m,n}\right]^{T}\in\mathbb{R}^{m\cdot n} }[/math] where we use [math]\displaystyle{ ``\cdot" }[/math] to dinstinguish [math]\displaystyle{ \mathbb{R}^{m\cdot n} }[/math] (a set of vectors with dimension [math]\displaystyle{ m\cdot n }[/math]) from [math]\displaystyle{ \mathbb{R}^{m\times n} }[/math] (the set of linear operators [math]\displaystyle{ V }[/math] such that [math]\displaystyle{ V:\mathbb{R}^{m}\rightarrow\mathbb{R}^{n}) }[/math].
- Let [math]\displaystyle{ A\in\mathbb{R}^{m\times n} }[/math] , then the induced 2-norm of [math]\displaystyle{ A }[/math] is defined as [math]\displaystyle{ ||A||_{2}=\sigma_{\max}(A) }[/math] where [math]\displaystyle{ \sigma_{\max}(A) }[/math] denotes the largest singular value of [math]\displaystyle{ A }[/math].
- If [math]\displaystyle{ A,B\in\mathbb{R}^{m\times n} }[/math] then [math]\displaystyle{ A\circ B }[/math] denotes the Hadamard product so that [math]\displaystyle{ \left[A\circ B\right]_{ij}=A_{ij}B_{ij};\ i\in\{1,...,m\},\ j\in\{1,...,n\} }[/math].
- [math]\displaystyle{ \mathcal{U}[a,b] }[/math] denotes the uniform distribution on [math]\displaystyle{ [a,b] }[/math] and [math]\displaystyle{ \mathcal{N}(\mu,\Sigma) }[/math] denotes the multivariate normal distribution.
- [math]\displaystyle{ \sigma_{l}:\mathbb{R\rightarrow\mathbb{R}},\ l\in\{1,...,L\} }[/math] is the activation function associated with layer [math]\displaystyle{ l }[/math]. [math]\displaystyle{ W_{l}^{*}\in\mathbb{R}^{d_{l}\times d_{l-1}},\ l\in\{0,...,L\} }[/math] denotes the weight matrix of this layer.
- The target network is defined as [math]\displaystyle{ F(x)=W_{l}^{*}\sigma_{l-1}(W_{l-1}^{*}\sigma_{l-1}(\cdots W_{2}^{*}\sigma_{1}(W_{1}^{*}x))) }[/math] and is just the functional representation of a neural network. It is assumed activation functions act componentwise on their inputs.
The authors in [18] also define the some more idiosyncratic objects:
- The number of weights in the [math]\displaystyle{ l^{\text{th}} }[/math] layer is denoted [math]\displaystyle{ D_{l}:=d_{l}d_{l-1} }[/math].
- A mask matrix [math]\displaystyle{ M\in[0,1]^{m\times n} }[/math] is just an [math]\displaystyle{ m\times n }[/math] valued matrix whose entries are identically [math]\displaystyle{ 0 }[/math] or [math]\displaystyle{ 1 }[/math].
- A pruned weight matrix corresponding to the weight matrix [math]\displaystyle{ W_{l}^{*} }[/math] of a fully connected network is given by [math]\displaystyle{ W_{l}=M_{l}\circ W_{l}^{*} }[/math] where [math]\displaystyle{ M_{l} }[/math] is a mask matrix.
- A pruning [math]\displaystyle{ f(x) }[/math] of the target network [math]\displaystyle{ F(x) }[/math] is defined as [math]\displaystyle{ f(x)=W_{l}\sigma_{l-1}(W_{l-1}\sigma_{l-1}(\cdots W_{2}\sigma_{1}(W_{1}x))) }[/math].
- Let [math]\displaystyle{ W_{l} }[/math] be a pruned weight matrix for layer [math]\displaystyle{ l }[/math]. The compression ratio of layer [math]\displaystyle{ l }[/math] is defined as [math]\displaystyle{ \gamma_{l}:=\frac{||\text{vec}(W_{l})||_{0}}{D_{l}} }[/math]
- [math]\displaystyle{ f(x) }[/math] is said to be [math]\displaystyle{ \epsilon }[/math]-close to [math]\displaystyle{ F(x) }[/math] iff [math]\displaystyle{ \sup_{x\in\mathcal{B}_{d_{0}}}||f(x)-F(x)||\lt \epsilon }[/math] where [math]\displaystyle{ \mathcal{B}_{d_{0}}:=\left\{ x\in\mathbb{R}^{d_{0}}\ |\ ||x||_{2}\leq1\right\} }[/math] denotes the [math]\displaystyle{ d_{0} }[/math] unit-ball with the Euclidean norm.
Intuition Behind the Objects
In general the objects defined above are either defined to formally express a pruned network, or to provide some measure of efficacy for a given pruned network. In the former category are mask matrices, pruned weight matrices and prunings of the target network. The latter consists of [math]\displaystyle{ \epsilon }[/math]-closeness and the compression ratio.
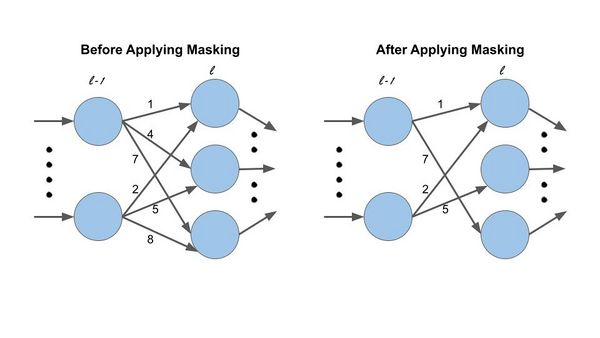
Intuitively, the mask matrix can be thought of as a “switch” which allows or blocks certain components of the previous layer to modify the input of the activation’s output. This can be seen with a toy example. Suppose that for some layer [math]\displaystyle{ l }[/math] of a FCN, the weight function is given as [math]\displaystyle{ W_{l}^{*}=\left[\begin{array}{cc} 1 & 2\\ 4 & 5\\ 7 & 8 \end{array}\right] }[/math] Now consider the mask matrix [math]\displaystyle{ M_{l}=\left[\begin{array}{cc} 1 & 1\\ 0 & 1\\ 1 & 0 \end{array}\right] }[/math] This mask induces a pruned weight matrix [math]\displaystyle{ W_{l} = M_{l} \circ W^*_{l} = \left[\begin{array}{cc} 1 & 1\\ 0 & 1\\ 1 & 0 \end{array}\right]\circ\left[\begin{array}{cc} 1 & 2\\ 4 & 5\\ 7 & 8 \end{array}\right]=\left[\begin{array}{cc} 1 & 2\\ 0 & 5\\ 7 & 0 \end{array}\right] }[/math] Now suppose the input from the previous layer is given by [math]\displaystyle{ x=[x_{1},x_{2}]^{T} }[/math], then [math]\displaystyle{ z:=W_{l}x=\left[\begin{array}{c} x_{1}+2x_{2}\\ 5x_{2}\\ 7x_{1} \end{array}\right]\neq\left[\begin{array}{c} x_{1}+2x_{2}\\ 4x_{1}+5x_{2}\\ 7x_{1}+8x_{2} \end{array}\right]=W_{l}^{*}x=:z^{*} }[/math]
Hence we see that the activation input is different between the pruned and unpruned weight matrices. But crucially, the [math]\displaystyle{ i^{\text{th}} }[/math] component [math]\displaystyle{ x_{i} }[/math] of the weight matrix input [math]\displaystyle{ x }[/math] has no influence of the [math]\displaystyle{ j^{\text{th}} }[/math] component [math]\displaystyle{ z_{j} }[/math] of the activation input [math]\displaystyle{ z }[/math] if [math]\displaystyle{ \left[M_{l}\right]_{ji}=0 }[/math], and the influence of the [math]\displaystyle{ x_{i} }[/math] on [math]\displaystyle{ z_{j} }[/math] is unaltered when [math]\displaystyle{ \left[M_{l}\right]_{ji}=0 }[/math]. This is what we mean by saying [math]\displaystyle{ M_{l} }[/math] switches — or prunes — connections in a weight matrix. Its effect is tantamount to severing a connection between the inputs of a weight matrix (or, outputs of the previous layer’s activation function) and the inputs of the layer’s activation function.
Since [math]\displaystyle{ W_{l}=M\circ W_{l}^{*} }[/math], [math]\displaystyle{ W_{l} }[/math] is naturally interpreted as the weight matrix of a network that has had its connections pruned by [math]\displaystyle{ M_{l} }[/math]. Finally, [math]\displaystyle{ f(x) }[/math] has the same same general architecture as [math]\displaystyle{ F(x) }[/math] — its activation functions, number of layers and nodes. If every [math]\displaystyle{ M_{ji}=0 }[/math] for some [math]\displaystyle{ i\in d_{l-1} }[/math], then it is clear the value of [math]\displaystyle{ x_{i}^{l} }[/math] will make no contribution to the vector [math]\displaystyle{ z }[/math]. However, strictly speaking the [math]\displaystyle{ i^{\text{th}} }[/math]node of layer [math]\displaystyle{ l-1 }[/math] is still part of the network — it’s just vestigial. are the same as [math]\displaystyle{ F(x) }[/math]. The only difference between [math]\displaystyle{ f(x) }[/math] and [math]\displaystyle{ F(x) }[/math] is that the former uses pruned weight vectors, while the latter uses the original, unpruned weight vectors. In this way it is clear that [math]\displaystyle{ f(x) }[/math] just represents a subnetwork of [math]\displaystyle{ F(x) }[/math] which has had its connections pruned as specified by the matrices [math]\displaystyle{ M_{l},\ l\in\{1,...,L\} }[/math].
The discussion above makes it clear that [math]\displaystyle{ f(x),M_{l},W_{l} }[/math] are defined as a means of formally representing a pruned subnetwork of some FCN. However, we ultimately wish to describe the efficacy of the pruned network. Of particular imporance are how much “smaller” the pruned subnetwork is compared to its corresponding FCN, and the discrepancies between the predictions of the pruned and FC network.
The former notion is captured by the compression ratio [math]\displaystyle{ \gamma_{l} }[/math]. In particular this ratio can be interpreted as the percentage of connections that are left in the neural network after pruning. So if [math]\displaystyle{ \gamma_{l}=0.18 }[/math], only [math]\displaystyle{ 18\% }[/math] of the original connections between layers [math]\displaystyle{ l }[/math] and [math]\displaystyle{ l-1 }[/math] remain. This can be seen in the extreme cases where a masking matrix [math]\displaystyle{ M_{l} }[/math] for some FC weight matrix [math]\displaystyle{ W_{l}^{*} }[/math] has entries that are identically [math]\displaystyle{ 0 }[/math] or [math]\displaystyle{ 1 }[/math]. In the first case, it is clear that every entry of [math]\displaystyle{ M_{l},\ \text{vec}(M_{l}) }[/math] are zero, so that [math]\displaystyle{ ||\text{vec}(W_{l})||_{0}=0 }[/math] and [math]\displaystyle{ \gamma_{l}=||\text{vec}(W_{l})||_{0}/D_{l}=0 }[/math]. Meanwhile if [math]\displaystyle{ M_{l} }[/math] has all entries equal to [math]\displaystyle{ 1 }[/math] then [math]\displaystyle{ ||\text{vec}(M_{l}\circ W_{l}^{*})||_{0}=d_{l}d_{l-1}=D_{k} }[/math] so [math]\displaystyle{ \gamma_{l}=1 }[/math]. Every other case falls in between these two extremes, since [math]\displaystyle{ 0\leq||\text{vec}(W_{l})||_{0}\leq D_{k} }[/math] clearly.
Returning to our toy example, we see that [math]\displaystyle{ W_{l}=\left[\begin{array}{cc} 1 & 2\\ 0 & 5\\ 7 & 0 \end{array}\right]\Rightarrow||\text{vec}(W_{l})||_{0}=4\Rightarrow\gamma_{l}=\frac{||\text{vec}(W_{l})||_{0}}{d_{l}\cdot d_{l-1}}=\frac{4}{3\cdot2}=0.667 }[/math] which again describes the percentage of connections which have not been pruned.
Finally [math]\displaystyle{ \epsilon }[/math]-closeness can be interpreted as a guaranteed accuracy. By selecting [math]\displaystyle{ x\in\mathcal{B}_{d_{0}} }[/math] that causes the largest discrepancy between the values of [math]\displaystyle{ f(\cdot) }[/math] and [math]\displaystyle{ F(\cdot) }[/math], [math]\displaystyle{ f(\cdot) }[/math] and [math]\displaystyle{ F(\cdot) }[/math] are [math]\displaystyle{ \epsilon }[/math]-close if even in the worst case scenario the discrepancy between the [math]\displaystyle{ f(\cdot) }[/math] and [math]\displaystyle{ F(\cdot) }[/math] is less than [math]\displaystyle{ \epsilon }[/math].
With this intuition in mind, the goal of a pruning algorithm can be cast in a more technical form: given a FCN [math]\displaystyle{ F(\cdot) }[/math], find a set of masking matrices [math]\displaystyle{ \{M_{1},...,M_{l}\} }[/math] so that for a given [math]\displaystyle{ \epsilon }[/math] the corresponding pruned network [math]\displaystyle{ f(\cdot) }[/math] has the smallest possible compression ratios [math]\displaystyle{ \{\gamma_{1},...,\gamma_{l}\} }[/math] while remaining [math]\displaystyle{ \epsilon }[/math]-close to [math]\displaystyle{ F(\cdot) }[/math].
The Main Result: Magnitude Based Pruning
Specifying a pruned subnetwork [math]\displaystyle{ f(\cdot) }[/math] is tantamount to determining a set of masking matrices. One approach for selecting [math]\displaystyle{ M }[/math] considered by the authors is so-called “magnitude based pruning”. This method begins by ordering the entries of a FC weight matrix [math]\displaystyle{ W_{l}^{*} }[/math] by magnitude [math]\displaystyle{ |W_{l}^{*}|_{i_{1},j_{1}}\leq\cdots\leq|W_{l}^{*}|_{i_{d_{l}},j_{d_{l}}} }[/math] where [math]\displaystyle{ i_{n},j_{n} }[/math] refer to the index of the entry in [math]\displaystyle{ W_{l}^{*} }[/math] with the [math]\displaystyle{ n^{\text{th}} }[/math] smallest magnitude ([math]\displaystyle{ n\in\{1,...,D_{k}\} }[/math]). Then [math]\displaystyle{ M_{l} }[/math] is set by first specifying the desired compression ratio [math]\displaystyle{ \gamma_{l} }[/math], setting the entries of [math]\displaystyle{ M_{l} }[/math] corresponding to the smallest [math]\displaystyle{ \lfloor\gamma_{l}D_{l}\rfloor }[/math] components of [math]\displaystyle{ W_{l}^{*} }[/math] to zero, and the rest to one.
With this context, we state the main result of the paper:
Theorem 1 of [18] : Suppose that [math]\displaystyle{ F }[/math] is a FC target network and that:
- (i)
- [math]\displaystyle{ \sigma_{l} }[/math] is Lipschitz continuous with constant [math]\displaystyle{ K_{l},\ \forall l\in\{1,...,L\} }[/math]
- (ii)
- [math]\displaystyle{ d:=\min\{d_{1},...,d_{L-1}\}\geq\max\{d_{0},d_{L}\} }[/math]
- (iii)
- The entries in [math]\displaystyle{ W_{k}^{*} }[/math] are iid following [math]\displaystyle{ \left[W_{k}^{*}\right]_{i,j}\sim\mathcal{U}\left[-\frac{K}{\sqrt{\max\{d_{l},d_{l-1}\}}},\frac{K}{\sqrt{\max\{d_{l},d_{l-1}\}}}\right];\ i\in\{1,...,d_{l}\},i\in\{1,...,d_{l-1}\} }[/math] where [math]\displaystyle{ K }[/math] is a fixed positive constant.
Let [math]\displaystyle{ \epsilon,\delta\gt 0,\alpha\in(0,1) }[/math] so that [math]\displaystyle{ d\geq\max\left\{ C_{1}^{\frac{1}{\alpha}},\left(\frac{C_{2}}{\epsilon}\right)^{\frac{1}{\alpha}},\left(\frac{C_{3}}{\delta}\right)^{\frac{1}{\alpha}},C_{4}+C_{5}\log\left(\frac{1}{\delta}\right)\right\} }[/math] For [math]\displaystyle{ C_{1},...,C_{5} }[/math] depending on values of [math]\displaystyle{ l,K_{l} }[/math]. Then with probability at least [math]\displaystyle{ 1-\delta }[/math], the subnetwork [math]\displaystyle{ f }[/math] of [math]\displaystyle{ F }[/math] with mask [math]\displaystyle{ M=\left\{ M_{1},...,M_{L}\ |\ M_{l}\in\{0,1\}^{d_{l}\times d_{l-1}}\right\} }[/math] pruning the smallest [math]\displaystyle{ \lfloor D_{l}^{1-\alpha}\rfloor }[/math] entries of [math]\displaystyle{ W_{l}^{*},\ l\in\{1,...,L\} }[/math] based on magnitude is [math]\displaystyle{ \epsilon }[/math]-close to [math]\displaystyle{ F }[/math], i.e. [math]\displaystyle{ \sup_{x\in\mathcal{B}_{d_{0}}}||f(x)-F(x)||_{2}\leq\epsilon }[/math]
We note that [math]\displaystyle{ \alpha }[/math] effectively specifies [math]\displaystyle{ \gamma_{l}=D_{l}^{-\alpha} }[/math], so although it is not directly stated in the theorem, the compression ratio is present.
Unpacking and Justifying the Assumptions:
As previously stated we will not provide a full characterization of the proof. Instead, we clarify why the authors made the three assumptions that appear in the theorem.
First, we comment on the Lipschitz continuity of [math]\displaystyle{ \sigma_{k} }[/math]. For our purposes function [math]\displaystyle{ g:\mathbb{R}^{n}\rightarrow\mathbb{R}^{n} }[/math] is Lipschitz continuous iff [math]\displaystyle{ ||g(x)-g(y)||_{2}\leq K||x-y||_{2} }[/math] for any [math]\displaystyle{ x,y\in\mathbb{R}^{n} }[/math] (see [20] for more details on Lipschitz continuity). The intuition when [math]\displaystyle{ g:\mathbb{R}\rightarrow\mathbb{R} }[/math] is that [math]\displaystyle{ g }[/math] is Lipschitz just when its value never changes quicker than the function [math]\displaystyle{ h(x)=Kx }[/math]. The reason the activation functions are Lipschitz continuous is just because the proof of the main theorem relies on random matrix theory and, in particular, the probability that the 2-norms of random matrices exceed certain bounds. By ensuring that [math]\displaystyle{ ||\sigma(z_{l}^{*})-\sigma(z_{l})||_{2}\leq K_{l}||W_{l}^{*}x_{l}-W_{l}x_{l}||_{2} }[/math] the authors are able to extend the results of bounding the difference between vectors under random matrices, to bounding the difference between vectors under non-linear transformations (see section 4 of [18]). So, the results of random matrix theory can be harnessed to prove the main results.
The second assumption is largely used to provide tighter bounds on the probabilities given in the relevant theorem. As such its role is mostly related to technical details (again see section 4 of [18]).
Finally, the third assumption is by far the most important assumption. As previously mentioned, the main proof relies on a few theorems imported from random matrix theory [18]. In particular, the main theorem heavily relies on [15, 17], of which the former only applies to independent, mean zero random matrices with finite fourth moments and the latter which applies to (sub-Gaussian) iid random matrices.
The first two assumptions are easy to justify. For the first assumption, we note that in practice most activation functions are Lipschitz continuous. For instance, the sigmoid, ReLU, tanh and softmax functions are all Lipschitz continuous with [math]\displaystyle{ K=1 }[/math] (see [19]). So this is clearly a reasonable assumption. The second assumption is even easier to justify. One can simply set all [math]\displaystyle{ d\geq\max\{d_{0},d_{l}\} }[/math] when designing the architecture of the FCN [math]\displaystyle{ F(\cdot) }[/math]. Hence the first two assumptions will almost always hold in practice.
Unlike the first two assumptions, the third assumption is not evidently the case. Assuming that [math]\displaystyle{ \{W_{l}^{*}\ |\ l\in\{1,...,L\}\} }[/math] are i.i.d. random is a priori strong assumption with no particularly strong justification. Given this difficulty, the authors essentially argue that because (1) there is no way to effectively measure how close weights are to independence, (2) some literature — namely [14, 15]— suggests that weights in a trained network do not deviate strongly from their initial values. However, in our view it is clear that this constitutes only a partial, if not promising, justification for assumption (iii). Consequently the most important assumption for the main theorem is also the least secure.
Future Works
Issues raised by Blalock et al argue that in general, the community surrounding neural network pruning research suffers from a lack of standardization. Definitions tend to be ambiguous and comparisons are difficult to make between performances of different pruning algorithms. Overall, this sector will see much more research and focus in the near future. This paper is a foundation for theoretical works regarding pruning both FCNs and CNNs. Importantly, since nearly all network architectures can be replaced by some combination of FCNs and CNNs, this paper has application in pruning many different architectures. Applying these results to past works by Frankle & Carbin in 2018 gives a method to determine an upper bound on the number of weights available for pruning in a given layer in order to maintain the desired error margin.
The paper’s analysis assumes that weights in the original network are independent. This assumption is not ideal, especially in CNNs. While the paper’s appendix discusses ways around it, no solution could be found. The authors suggest that an in-depth study of this assumption is warranted in the future. Another topic not explored fully is using gradients of the weights in the original network to determine more optimal pruning algorithms.
References
[1] Baykal, C., Liebenwein, L., Gilitschenski, I., Feldman, D., and Rus, D. Sipping neural networks: Sensitivity informed provable pruning of neural networks. arXiv preprint arXiv:1910.05422, 2019b.
[2] Frankle, J. and Carbin, M. The lottery ticket hypothesis: Finding sparse, trainable neural networks. International Conference on Learning Representations, 2018.
[3] Han, S., Mao, H., and Dally, W. J. Deep compression: Compressing deep neural networks with pruning, trained quantization and Huffman coding. International Conference on Learning Representations, 2015a.
[4] Hu, H., Peng, R., Tai, Y.-W., and Tang, C.-K. Network trimming: A data-driven neuron pruning approach towards efficient deep architectures. arXiv preprint arXiv:1607.03250, 2016.
[5] LeCun, Y., Denker, J. S., Solla, S. A., Howard, R. E., and Jackel, L. D. Optimal brain damage. Advances in Neural Information Processing Systems, volume 2, pp. 598–605, 1989
[6] Li, H., Kadav, A., Durdanovic, I., Samet, H., and Graf, H. P. Pruning filters for efficient convnets. International Conference on Learning Representations, 2016.
[7] Liebenwein, L., Baykal, C., Lang, H., Feldman, D., and Rus, D. Provable filter pruning for efficient neural networks. International Conference on Learning Representations, 2020
[8] Pensia, A., Rajput, S., Nagle, A., Vishwakarma, H., and Papailiopoulos, D. Optimal lottery tickets via subset sum: Logarithmic over-parameterization is sufficient. Advances in Neural Information Processing Systems, 33, 2020.
[9] Orseau, L., Hutter, M., and Rivasplata, O. Logarithmic pruning is all you need. Advances in Neural Information Processing Systems, 33, 2020.
[10] Ramanujan, V., Wortsman, M., Kembhavi, A., Farhadi, A., and Rastegari, M. What’s hidden in a randomly weighted neural network? Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 11893–11902, 2020
[11] Ye, M., Gong, C., Nie, L., Zhou, D., Klivans, A., and Liu, Q. Good subnetworks provably exist: Pruning via greedy forward selection. In International Conference on Machine Learning, pp. 10820–10830, 2020a.
[12] Ye, M., Wu, L., and Liu, Q. Greedy optimization provably wins the lottery: Logarithmic number of winning tickets is enough. arXiv preprint arXiv:2010.15969, 2020b.
[13] Blalock, D., Ortiz, J.J.G., Frankle, J., Guttag, J. What is the State of Neural Network Pruning?. arXiv preprint arXiv:2003.03033, 2020.
[14] Yu Bai and Jason D. Lee. Beyond linearization: On quadratic and higher-order approximation of wide neural networks, 2020.
[15] H. A. David and H. N. Nagaraja. Order Statistics. American Cancer Society, 2004.
[16] Jacot, A., Gabriel, F., Hongler, C. Neural tangent kernel: convergence and generalization in neural networks. Proceedings of the 53rd Annual ACM SIGACT Symposium on Theory of Computing, 2021.
[17] Latala, R. Some estimates of norms of random matrices. Proceedings of the American Mathematical Society, 133(5):1273-1282, 2005.
[18] Qian, X., Klabjan, D. A probabilistic approach to neural network pruning, 2021.
[19] Scaman, K., Virmaux, A. Lipschitz regularity of deep neural networks: Analysis and efficient estimation. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, NIPS'18, pages 3839 - 3848. Curran Associates Inc., 2018.
[20] O'Searcoid, M. Metric Spaces. Springer Undergraduate Mathematics Series. Springer, 1 edition, 2006.