Streaming Bayesian Inference for Crowdsourced Classification
Group 4 Paper Presentation Summary
By Jonathan Chow, Nyle Dharani, Ildar Nasirov
Motivation
Crowdsourcing can be a useful tool for data generation in classification projects. Often this takes the form of online questions which many respondents will manually answer for payment. One example of this is Amazon’s Mechanical Turk.
The primary limitation with this form of acquiring data is that respondents are liable to submit incorrect responses.
The integrity of the data is then limited by how well ground-truth can be determined. The primary method for doing so is probabilistic inference. However, current methods are computationally expensive, lack theoretical guarantees, or are limited to specific settings.
Dawid-Skene Model for Crowdsourcing
The one-coin Dawid-Skene model is popular for contextualizing crowdsourcing problems. For task [math]\displaystyle{ i }[/math] in set [math]\displaystyle{ M }[/math], let the ground-truth be the binary [math]\displaystyle{ y_i = {\pm 1} }[/math]. We get labels [math]\displaystyle{ X = {x_{ij}} }[/math] where [math]\displaystyle{ j \in N }[/math] is the index for that worker.
At each time step [math]\displaystyle{ t }[/math], a worker [math]\displaystyle{ j = a(t) }[/math] provides their label for an assigned task [math]\displaystyle{ i }[/math]. We denote responses up to time [math]\displaystyle{ t }[/math] via superscript.
We let [math]\displaystyle{ x_{ij} = 0 }[/math] if worker [math]\displaystyle{ j }[/math] has not completed task [math]\displaystyle{ i }[/math]. We assume that [math]\displaystyle{ P(x_{ij} = y_i) = p_j }[/math]. This implies that each worker is independent and has equal probability of correct labelling regardless of task. In crowdsourcing the data, we must determine how workers are assigned to tasks. We introduce two methods.
Under uniform sampling, workers are allocated to tasks such that each task is completed by the same number of workers, rounded to the nearest integer, and no worker completes a task more than once. This policy is given by
Under uncertainty sampling, we assign more workers to tasks that are less certain. Assuming, we are able to estimate the posterior probability of ground-truth, we can allocate workers to the task with the lowest probability of falling into the predicted class. This policy is given by
We then need to aggregate the data. The simple method of majority voting makes predictions for a given task based on the class the most workers have assigned it, [math]\displaystyle{ \hat{y}_i = sign\{\sum_{j \in N_i} x_{ij}\} }[/math].
Streaming Bayesian Inference for Crowdsourced Classification
The aim of the SBIC algorithm is to estimate the posterior probability, [math]\displaystyle{ P(y, p | X^t, \theta) }[/math] where [math]\displaystyle{ X^t }[/math] are the observed responses at time [math]\displaystyle{ t }[/math] and [math]\displaystyle{ \theta }[/math] is our prior. We can then generate predictions [math]\displaystyle{ \hat{y}^t }[/math] as the marginal probability over each [math]\displaystyle{ y_i }[/math] given [math]\displaystyle{ X^t }[/math], and [math]\displaystyle{ \theta }[/math].
We factor [math]\displaystyle{ P(y, p | X^t, \theta) }[/math] as [math]\displaystyle{ \prod_{I \in M} \mu_i^t (y_i) \prod_{j \in N} \nu_j^t (p_j) }[/math] where [math]\displaystyle{ \mu_i^t }[/math] corresponds to each task and [math]\displaystyle{ \nu_j^t }[/math] to each worker.
We then sequentially optimize the factors [math]\displaystyle{ \mu^t }[/math] and [math]\displaystyle{ \nu^t }[/math]. We begin by assuming that the worker accuracy follows a beta distribution with parameters [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math]. Initialize the task factors [math]\displaystyle{ \mu_i^0(+1) = q }[/math] and [math]\displaystyle{ \mu_i^0(-1) = 1 – q }[/math] for all [math]\displaystyle{ i }[/math].
When a new label is observed at time [math]\displaystyle{ t }[/math], we update the [math]\displaystyle{ \nu_j^t }[/math] of worker [math]\displaystyle{ j }[/math]. We then update [math]\displaystyle{ \mu_i }[/math]. These updates are given by
where [math]\displaystyle{ \overline{p}_j^t = \frac{\sum_{i \in M_j^{t - 1}} \mu_i^{t - 1}(x_ij) + \alpha}{|M_j^{t - 1}| + \alpha + \beta } }[/math].
We choose our predictions to be the maximum [math]\displaystyle{ \mu_i^t(k) }[/math] for [math]\displaystyle{ k=-1,1 }[/math].
Depending on our ordering of labels [math]\displaystyle{ X }[/math], we can select for different applications.
Fast SBIC
The pseudocode for Fast SBIC is shown below.

As the name implies, the goal with this algorithm is speed. To facilitate this, we leave the order of [math]\displaystyle{ X }[/math] unchanged.
We express [math]\displaystyle{ \mu_i^t }[/math] in terms of its log-odds
where [math]\displaystyle{ x_i^0 = log(\frac{q}{1 - q}) }[/math].
The product chain then becomes a summation and removes the need to normalize each [math]\displaystyle{ \mu_i^t }[/math]. We use these log-odds to compute worker accuracy.
where [math]\displaystyle{ sig(z_i^{t-1}) := \frac{1}{1 + exp(-z_i^{t - 1})} = \mu_i^{t - 1}(+1) }[/math]
The final predictions are made by choosing class [math]\displaystyle{ \hat{y}_i^T = sign(z_i^T) }[/math]. We see later that Fast SBIC has similar computational speed to majority voting.
Sorted SBIC
To increase the accuracy of the SBIC algorithm in exchange for computational efficiency, we run the algorithm in parallel giving labels in different orders. The pseudocode for this algorithm is given below.

From the general discussion of SBIC, we know that predictions on task [math]\displaystyle{ i }[/math] are more accurate toward the end of the collection process. This is a result of observing more data points and having run more updates on [math]\displaystyle{ \mu_i^t }[/math] and [math]\displaystyle{ \nu_j^t }[/math] to move them further from their prior. This means that task [math]\displaystyle{ i }[/math] is predicted more accurately when its corresponding labels are seen closer to the end of the process.
We take advantage of this property by maintaining a distinct “view” of the log-odds for each task. When a label is observed, we update views for all tasks except the one for which the label was observed. At the end of the collection process, we process skipped labels. When run online, this process must be repeated at every timestep.
We see that sorted SBIC is slower than Fast SBIC by a factor of M, the number of tasks.
Theoretical Analysis
The authors prove an exponential relationship between the error probability and number of labels per task. The two theorems, for the different sampling regimes, are presented below.


Empirical Analysis
The SBIC algorithm is run on five real-world binary classification datasets. The results can be found in the table below. Other algorithms in the comparison are, from left to right, majority voting, expectation-maximization, mean-field, belief-propagation, montecarlo sampling, and triangular estimation.
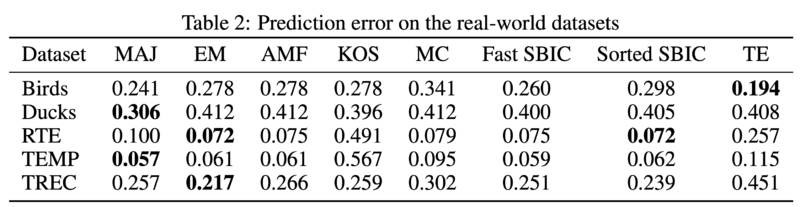
In bold are the best performing algorithms for each dataset. We see that both versions of the SBIC algorithm are competitive, having similar prediction error to EM, AMF, and MC. All are considered state-of-the-art Bayesian algorithms.
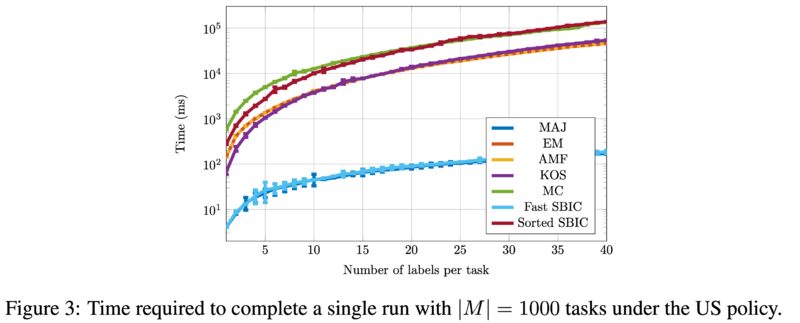
The figure below shows the average time required to simulate predictions on synthetic data under an uncertainty sampling policy. We see that Fast SBIC is comparable to majority voting and significantly faster than the other algorithms. This speed improvement, coupled with comparable accuracy, makes the Fast SBIC algorithm powerful.
Conclusion and Future Research
In conclusion, we have seen that SBIC is computationally efficient, accurate in practice, and has theoretical guarantees. In future, the authors intend to extend the algorithm to the multi-class case.
Critique
In crowdsourcing data, the cost associated with collecting additional labels is not usually prohibitively expensive. As a result, if there is concern over ground-truth, paying for additional data to ensure [math]\displaystyle{ X }[/math] is sufficiently dense may be the desired response as opposed to sacrificing ground-truth accuracy. This may result in the SBIC algorithm being less practically useful than intended.
References
[1] Manino, Tran-Thanh, and Jennings. Streaming Bayesian Inference for Crowdsourced Classification. 33rd Conference on Neural Information Processing Systems, 2019