Spherical CNNs: Difference between revisions
| Line 23: | Line 23: | ||
= Related Work = | = Related Work = | ||
It is well understood that the power of CNNs stems in large part from their ability to exploit | |||
(translational) symmetries though a combination of weight sharing and translation equivariance. | |||
It thus becomes natural to consider generalizations that exploit larger groups of symmetries, and | |||
indeed this has been the subject of several recent papers by Gens and Domingos (2014); Olah (2014); | |||
Dieleman et al. (2015; 2016); Cohen and Welling (2016); Ravanbakhsh et al. (2017); Zaheer et al. | |||
(2017b); Guttenberg et al. (2016); Cohen and Welling (2017). With the exception of SO(2)-steerable | |||
networks (Worrall et al., 2017; Weiler et al., 2017), these networks are all limited to discrete groups, | |||
such as discrete rotations acting on planar images or permutations acting on point clouds. Other very | |||
recent work is concerned with the analysis of spherical images, but does not define an equivariant | |||
architecture (Su and Grauman, 2017; Boomsma and Frellsen, 2017). Our work is the first to achieve | |||
equivariance to a continuous, non-commutative group (SO(3)), and the first to use the generalized | |||
Fourier transform for fast group correlation. A preliminary version of this work appeared as Cohen | |||
et al. (2017). | |||
To efficiently perform cross-correlations on the sphere and rotation group, we use generalized FFT | |||
algorithms. Generalized Fourier analysis, sometimes called abstract- or noncommutative harmonic | |||
analysis, has a long history in mathematics and many books have been written on the subject | |||
(Sugiura, 1990; Taylor, 1986; Folland, 1995). For a good engineering-oriented treatment which | |||
covers generalized FFT algorithms, see (Chirikjian and Kyatkin, 2001). Other important works | |||
include (Driscoll and Healy, 1994; Healy et al., 2003; Potts et al., 1998; Kunis and Potts, 2003; Drake | |||
et al., 2008; Maslen, 1998; Rockmore, 2004; Kostelec and Rockmore, 2007; 2008; Potts et al., 2009; | |||
Makadia et al., 2007; Gutman et al., 2008). | |||
= Correlations on the Sphere and Rotation Group = | = Correlations on the Sphere and Rotation Group = | ||
Latest revision as of 22:53, 20 April 2018
Introduction
Convolutional Neural Networks (CNNs), or network architectures involving CNNs, are the current state of the art for learning 2D image processing tasks such as semantic segmentation and object detection. CNNs work well in large part due to the property of being translationally equivariant. This property allows a network trained to detect a certain type of object to still detect the object even if it is translated to another position in the image. However, this does not correspond well to spherical signals since projecting a spherical signal onto a plane will result in distortions, as demonstrated in Figure 1. There are many different types of spherical projections onto a 2D plane, as most people know from the various types of world maps, none of which provide all the necessary properties for rotation-invariant learning. Applications where spherical CNNs can be applied include omnidirectional vision for robots, molecular regression problems, and weather/climate modelling.
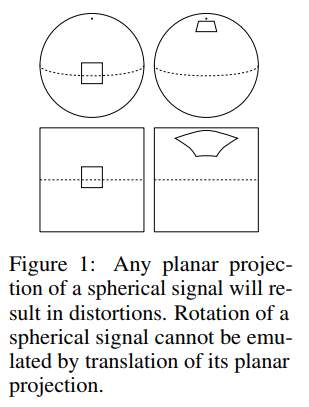
The implementation of a spherical CNN is challenging mainly because no perfectly symmetrical grids for the sphere exists which makes it difficult to define the rotation of a spherical filter by one pixel and the computational efficiency of the system.
The main contributions of this paper are the following:
- The theory of spherical CNNs. The authors provide mathematical foundations for translation equivariance under a spherical framework.
- The first automatically differentiable implementation of the generalized Fourier transform for [math]\displaystyle{ S^2 }[/math] and SO(3). The provided PyTorch code by the authors is easy to use, fast, and memory efficient.
- The first empirical support for the utility of spherical CNNs for rotation-invariant learning problems. They apply it to spherical MNIST, 3D shape classification, and molecular energy regression.
Note: Translationally equivariant
Equivariant to translation means that a translation of input features results in an equivalent translation of outputs. So if your pattern 0,3,2,0,0 on the input results in 0,1,0,0 in the output, then the pattern 0,0,3,2,0 might lead to 0,0,1,0.
Notation
Below are listed several important terms:
- Unit Sphere [math]\displaystyle{ S^2 }[/math] is defined as a sphere where all of its points are distance of 1 from the origin. The unit sphere can be parameterized by the spherical coordinates [math]\displaystyle{ \alpha ∈ [0, 2π] }[/math] and [math]\displaystyle{ β ∈ [0, π] }[/math]. This is a two-dimensional manifold with respect to [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ β }[/math].
- [math]\displaystyle{ S^2 }[/math] Sphere The three dimensional surface from a 3D sphere
- Spherical Signals In the paper spherical images and filters are modeled as continuous functions [math]\displaystyle{ f : s^2 → \mathbb{R}^K }[/math]. K is the number of channels. Such as how RGB images have 3 channels a spherical signal can have numerous channels describing the data. Examples of channels which were used can be found in the experiments section.
- Rotations - SO(3) The group of 3D rotations on an [math]\displaystyle{ S^2 }[/math] sphere. Sometimes called the "special orthogonal group". In this paper the ZYZ-Euler parameterization is used to represent SO(3) rotations with [math]\displaystyle{ \alpha, \beta }[/math], and [math]\displaystyle{ \gamma }[/math]. Any rotation can be broken down into first a rotation ([math]\displaystyle{ \alpha }[/math]) about the Z-axis, then a rotation ([math]\displaystyle{ \beta }[/math]) about the new Y-axis (Y'), followed by a rotation ([math]\displaystyle{ \gamma }[/math]) about the new Z axis (Z"). [In the rest of this paper, to integrate functions on SO(3), the authors use a rotationally invariant probability measure on the Borel subsets of SO(3). This measure is an example of a Haar measure. Haar measures generalize the idea of rotationally invariant probability measures to general topological groups. For more on Haar measures, see (Feldman 2002) ]
Related Work
It is well understood that the power of CNNs stems in large part from their ability to exploit (translational) symmetries though a combination of weight sharing and translation equivariance. It thus becomes natural to consider generalizations that exploit larger groups of symmetries, and indeed this has been the subject of several recent papers by Gens and Domingos (2014); Olah (2014); Dieleman et al. (2015; 2016); Cohen and Welling (2016); Ravanbakhsh et al. (2017); Zaheer et al. (2017b); Guttenberg et al. (2016); Cohen and Welling (2017). With the exception of SO(2)-steerable networks (Worrall et al., 2017; Weiler et al., 2017), these networks are all limited to discrete groups, such as discrete rotations acting on planar images or permutations acting on point clouds. Other very recent work is concerned with the analysis of spherical images, but does not define an equivariant architecture (Su and Grauman, 2017; Boomsma and Frellsen, 2017). Our work is the first to achieve equivariance to a continuous, non-commutative group (SO(3)), and the first to use the generalized Fourier transform for fast group correlation. A preliminary version of this work appeared as Cohen et al. (2017). To efficiently perform cross-correlations on the sphere and rotation group, we use generalized FFT algorithms. Generalized Fourier analysis, sometimes called abstract- or noncommutative harmonic analysis, has a long history in mathematics and many books have been written on the subject (Sugiura, 1990; Taylor, 1986; Folland, 1995). For a good engineering-oriented treatment which covers generalized FFT algorithms, see (Chirikjian and Kyatkin, 2001). Other important works include (Driscoll and Healy, 1994; Healy et al., 2003; Potts et al., 1998; Kunis and Potts, 2003; Drake et al., 2008; Maslen, 1998; Rockmore, 2004; Kostelec and Rockmore, 2007; 2008; Potts et al., 2009; Makadia et al., 2007; Gutman et al., 2008).
Correlations on the Sphere and Rotation Group
Spherical correlation is like planar correlation except instead of translation, there is rotation. The definitions for each are provided as follows:
Planar correlation The value of the output feature map at translation [math]\displaystyle{ \small x ∈ Z^2 }[/math] is computed as an inner product between the input feature map and a filter, shifted by [math]\displaystyle{ \small x }[/math].
The unit sphere [math]\displaystyle{ S^2 }[/math] can be defined as the set of points [math]\displaystyle{ x ∈ R^3 }[/math] with norm 1. It is a two-dimensional manifold, which can be parameterized by spherical coordinates α ∈ [0, 2π] and β ∈ [0, π].
Spherical Signals We model spherical images and filters as continuous functions f : [math]\displaystyle{ S^2 }[/math] → [math]\displaystyle{ R^K }[/math], where K is the number of channels.
Rotations The set of rotations in three dimensions is called SO(3), the “special orthogonal group”. Rotations can be represented by 3 × 3 matrices that preserve distance (i.e. ||Rx|| = ||x||) and orientation (det(R) = +1). If we represent points on the sphere as 3D unit vectors x, we can perform a rotation using the matrix-vector product Rx. The rotation group SO(3) is a three-dimensional manifold, and can be parameterized by ZYZ-Euler angles α ∈ [0, 2π], β ∈ [0, π], and γ ∈ [0, 2π].
Spherical correlation The value of the output feature map evaluated at rotation [math]\displaystyle{ \small R ∈ SO(3) }[/math] is computed as an inner product between the input feature map and a filter, rotated by [math]\displaystyle{ \small R }[/math].
Rotation of Spherical Signals The paper introduces the rotation operator [math]\displaystyle{ L_R }[/math]. The rotation operator simply rotates a function (which allows us to rotate the the spherical filters) by [math]\displaystyle{ R^{-1} }[/math]. With this definition we have the property that [math]\displaystyle{ L_{RR'} = L_R L_{R'} }[/math].
Inner Products The inner product of spherical signals is simply the integral summation on the vector space over the entire sphere.
[math]\displaystyle{ \langle\psi , f \rangle = \int_{S^2} \sum_{k=1}^K \psi_k (x)f_k (x)dx }[/math]
[math]\displaystyle{ dx }[/math] here is SO(3) rotation invariant and is equivalent to [math]\displaystyle{ d \alpha sin(\beta) d \beta / 4 \pi }[/math] in spherical coordinates. This comes from the ZYZ-Euler paramaterization where any rotation can be broken down into first a rotation about the Z-axis, then a rotation about the new Y-axis (Y'), followed by a rotation about the new Z axis (Z"). More details on this are given in Appendix A in the paper.
By this definition, the invariance of the inner product is then guaranteed for any rotation [math]\displaystyle{ R ∈ SO(3) }[/math]. In other words, when subjected to rotations, the volume under a spherical heightmap does not change. The following equations show that [math]\displaystyle{ L_R }[/math] has a distinct adjoint ([math]\displaystyle{ L_{R^{-1}} }[/math]) and that [math]\displaystyle{ L_R }[/math] is unitary and thus preserves orthogonality and distances.
[math]\displaystyle{ \langle L_R \psi \,, f \rangle = \int_{S^2} \sum_{k=1}^K \psi_k (R^{-1} x)f_k (x)dx }[/math]
- [math]\displaystyle{ = \int_{S^2} \sum_{k=1}^K \psi_k (x)f_k (Rx)dx }[/math]
- [math]\displaystyle{ = \langle \psi , L_{R^{-1}} f \rangle }[/math]
Spherical Correlation With the above knowledge the definition of spherical correlation of two signals [math]\displaystyle{ f }[/math] and [math]\displaystyle{ \psi }[/math] is:
[math]\displaystyle{ [\psi \star f](R) = \langle L_R \psi \,, f \rangle = \int_{S^2} \sum_{k=1}^K \psi_k (R^{-1} x)f_k (x)dx }[/math]
The output of the above equation is a function on SO(3). This can be thought of as for each rotation combination of [math]\displaystyle{ \alpha , \beta , \gamma }[/math] there is a different volume under the correlation. The authors make a point of noting that previous work by Driscoll and Healey only ensures circular symmetries about the Z axis and their new formulation ensures symmetry about any rotation.
Rotation of SO(3) Signals The first layer of Spherical CNNs take a function on the sphere ([math]\displaystyle{ S^2 }[/math]) and output a function on SO(3). Therefore, if a Spherical CNN with more than one layer is going to be built there needs to be a way to find the correlation between two signals on SO(3). The authors then generalize the rotation operator ([math]\displaystyle{ L_R }[/math]) to encompass acting on signals from SO(3). This new definition of [math]\displaystyle{ L_R }[/math] is as follows: (where [math]\displaystyle{ R^{-1}Q }[/math] is a composition of rotations, i.e. multiplication of rotation matrices)
[math]\displaystyle{ [L_Rf](Q)=f(R^{-1} Q) }[/math]
Rotation Group Correlation The correlation of two signals ([math]\displaystyle{ f,\psi }[/math]) on SO(3) with K channels is defined as the following:
[math]\displaystyle{ [\psi \star f](R) = \langle L_R \psi , f \rangle = \int_{SO(3)} \sum_{k=1}^K \psi_k (R^{-1} Q)f_k (Q)dQ }[/math]
where dQ represents the ZYZ-Euler angles [math]\displaystyle{ d \alpha sin(\beta) d \beta d \gamma / 8 \pi^2 }[/math]. A complete derivation of this can be found in Appendix A.
Equivariance The equivariance for the rotation group correlation is similarly demonstrated. A layer is equivariant if for some operator [math]\displaystyle{ T_R }[/math], [math]\displaystyle{ \Phi \circ L_R = T_R \circ \Phi }[/math], and:
[math]\displaystyle{ [\psi \star [L_Qf]](R) = \langle L_R \psi , L_Qf \rangle = \langle L_{Q^{-1} R} \psi , f \rangle = [\psi \star f](Q^{-1}R) = [L_Q[\psi \star f]](R) }[/math].
Implementation with GFFT
The authors leverage the Generalized Fourier Transform (GFT) and Generalized Fast Fourier Transform (GFFT) algorithms to compute the correlations outlined in the previous section. The Fast Fourier Transform (FFT) can compute correlations and convolutions efficiently by means of the Fourier theorem. The Fourier theorem states that a continuous periodic function can be expressed as a sum of a series of sine or cosine terms (called Fourier coefficients). The FT can be generalized to [math]\displaystyle{ S^2 }[/math] and SO(3) and is then called the GFT. The GFT is a linear projection of a function onto orthogonal basis functions. The basis functions are a set of irreducible unitary representations for a group (such as for [math]\displaystyle{ S^2 }[/math] or SO(3)). For [math]\displaystyle{ S^2 }[/math] the basis functions are the spherical harmonics [math]\displaystyle{ Y_m^l(x) }[/math]. For SO(3) these basis functions are called the Wigner D-functions [math]\displaystyle{ D_{mn}^l(R) }[/math]. For both sets of functions the indices are restricted to [math]\displaystyle{ l\geq0 }[/math] and [math]\displaystyle{ -l \leq m,n \geq l }[/math]. The Wigner D-functions are also orthogonal so the Fourier coefficients can be computed by the inner product with the Wigner D-functions (See Appendix C for complete proof). The Wigner D-functions are complete which means that any function (which is well behaved) on SO(3) can be expressed as a linear combination of the Wigner D-functions. The GFT of a function on SO(3) is thus:
[math]\displaystyle{ \hat{f^l} = \int_X f(x) D^l(x)dx }[/math]
where [math]\displaystyle{ \hat{f} }[/math] represents the Fourier coefficients. For [math]\displaystyle{ S^2 }[/math] we have the same equation but with the basis functions [math]\displaystyle{ Y^l }[/math].
The inverse SO(3) Fourier transform is:
[math]\displaystyle{ f(R)=[\mathcal{F}^{-1} \hat{f}](R) = \sum_{l=0}^b (2l + 1) \sum_{m=-l}^l \sum_{n=-l}^l \hat{f_{mn}^l} D_{mn}^l(R) }[/math]
The bandwidth b represents the maximum frequency and is related to the resolution of the spatial grid. Kostelec and Rockmore are referenced for more knowledge on this topic.
The authors give proofs (Appendix D) that the SO(3) correlation satisfies the Fourier theorem and the [math]\displaystyle{ S^2 }[/math] correlation of spherical signals can be computed by the outer products of the [math]\displaystyle{ S^2 }[/math]-FTs (Shown in Figure 2).
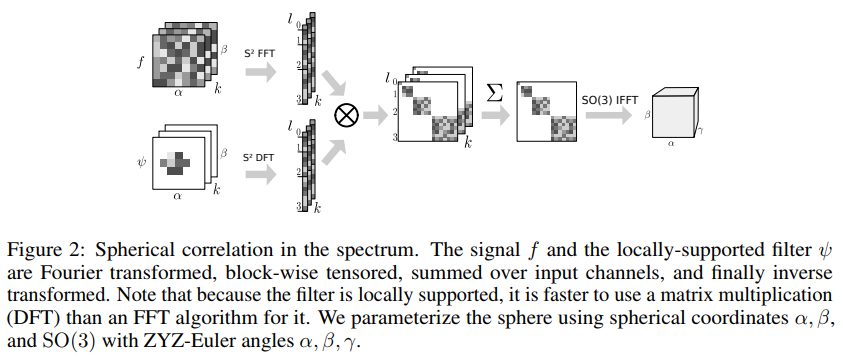
A high-level, approximately-correct, somewhat intuitive explanation of the above figure is that the spherical signal [math]\displaystyle{ f }[/math] parameterized over [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] having [math]\displaystyle{ k }[/math] channels is being correlated with a single filter [math]\displaystyle{ \psi }[/math] with the end result being a 3-D feature map on SO(3) (parameterized by Euler angles). The size in [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] is the kernel size. The index [math]\displaystyle{ l }[/math] going from 0 to 3 correspond the degree of the basis functions used in the Fourier transform. As the degree goes up, so does the dimensionality of vector-valued (for spheres) basis functions. The signals involved are discrete, so the maximum degree (analogous to number of Fourier coefficients) depends on the resolution of the signal. The SO(3) basis functions are matrix-valued, but because [math]\displaystyle{ S^2 = SO(3)/SO(2) }[/math], it ends up that the sphere basis functions correspond to one column in the matrix-valued SO(3) basis functions, which is why the outer product in the figure works.
The GFFT algorithm details are taken from Kostelec and Rockmore. The authors claim they have the first automatically differentiable implementation of the GFT for [math]\displaystyle{ S^2 }[/math] and SO(3). The authors do not provide any run time comparisons for real time applications (they just mentioned that FFT can be computed in [math]\displaystyle{ O(n\mathrm{log}n) }[/math] time as opposed to [math]\displaystyle{ O(n^2) }[/math] for FT) or any comparisons on training times with/without GFFT. However, they do provide the source code of their implementation at: https://github.com/jonas-koehler/s2cnn.
Experiments
The authors provide several experiments. The first set of experiments are designed to show the numerical stability and accuracy of the outlined methods. The second group of experiments demonstrates how the algorithms can be applied to current problem domains.
Equivariance Error
In this experiment the authors try to show experimentally that their theory of equivariance holds. They express that they had doubts about the equivariance in practice due to potential discretization artifacts since equivariance was proven for the continuous case, with the potential consequence of equivariance not holding being that the weight sharing scheme becomes less effective. The experiment is set up by first testing the equivariance of the SO(3) correlation at different resolutions. 500 random rotations and feature maps (with 10 channels) are sampled. They then calculate the approximation error [math]\displaystyle{ \small\Delta = \dfrac{1}{n} \sum_{i=1}^n std(L_{R_i} \Phi(f_i) - \phi(L_{R_i} f_i))/std(\Phi(f_i)) }[/math] Note: The authors do not mention what the std function is however it is likely the standard deviation function as 'std' is the command for standard deviation in MATLAB. [math]\displaystyle{ \Phi }[/math] is a composition of SO(3) correlation layers with filters which have been randomly initialized. The authors mention that they were expecting [math]\displaystyle{ \Delta }[/math] to be zero in the case of perfect equivariance. This is due to, as proven earlier, the following two terms equaling each other in the continuous case: [math]\displaystyle{ \small L_{R_i} \Phi(f_i) - \phi(L_{R_i} f_i) }[/math]. The results are shown in Figure 3.
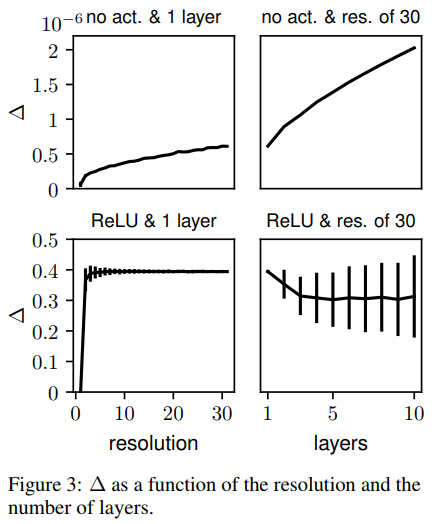
[math]\displaystyle{ \Delta }[/math] only grows with resolution/layers when there is no activation function. With ReLU activation the error stays constant once slightly higher than 0 resolution. The authors indicate that the error must therefore be from the feature map rotation since this type of error is exact only for bandlimited functions.
MNIST Data
The experiment using MNIST data was created by projecting MNIST digits onto a sphere using stereographic projection to create the resulting images as seen in Figure 4.

The authors created two datasets, one with the projected digits and the other with the same projected digits which were then subjected to a random rotation. The spherical CNN architecture used was [math]\displaystyle{ \small S^2 }[/math]conv-ReLU-SO(3)conv-ReLU-FC-softmax and was attempted with bandwidths of 30,10,6 and 20,40,10 channels for each layer respectively. This model was compared to a baseline CNN with layers conv-ReLU-conv-ReLU-FC-softmax with 5x5 filters, 32,64,10 channels and stride of 3. For comparison this leads to approximately 68K parameters for the baseline and 58K parameters for the spherical CNN. Results can be seen in Table 1. It is clear from the results that the spherical CNN architecture made the network rotationally invariant. Performance on the rotated set is almost identical to the non-rotated set. This is true even when trained on the non-rotated set and tested on the rotated set. Compare this to the non-spherical architecture which becomes unusable when rotating the digits.

SHREC17
The SHREC dataset contains 3D models from the ShapeNet dataset which are classified into categories. It consists of a regularly aligned dataset and a rotated dataset. The models from the SHREC17 dataset were projected onto a sphere by means of raycasting. Different properties of the objects obtained from the raycast of the original model and the convex hull of the model make up the different channels which are input into the spherical CNN.
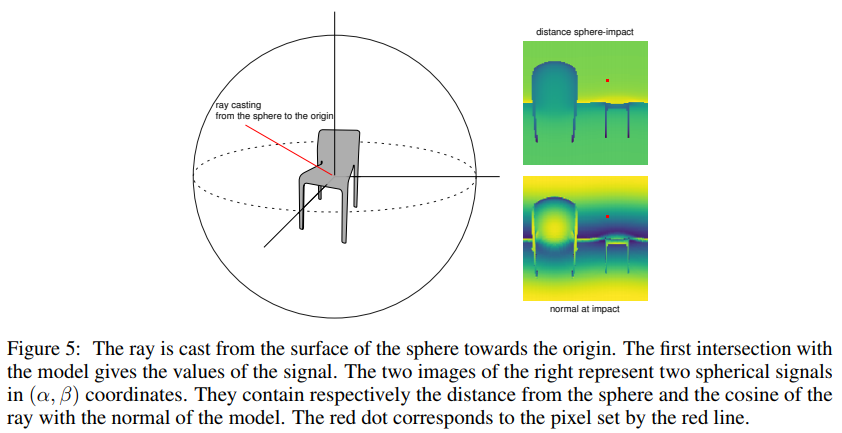
The network architecture used is an initial [math]\displaystyle{ \small S^2 }[/math]conv-BN-ReLU block which is followed by two SO(3)conv-BN-ReLU blocks. The output is then fed into a MaxPool-BN block then a linear layer to the output for final classification. An important note is that the max pooling happens over the group SO(3): if [math]\displaystyle{ f_k }[/math] is the [math]\displaystyle{ \small k }[/math]-th filter in the final layer, the result of pooling is [math]\displaystyle{ max_{x \in SO(3)} f_k(x) }[/math]. 50 features were used for the [math]\displaystyle{ \small S^2 }[/math] layer, while the two SO(3) layers used 70 and 350 features. Additionally, for each layer the resolution [math]\displaystyle{ \small b }[/math] was reduced from 128,32,22 to 7 in the final layer. The architecture for this experiment has ~1.4M parameters, far exceeding the scale of the spherical CNNs in the other experiments.
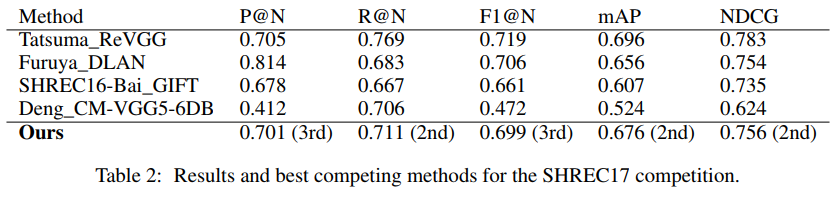
This architecture achieves state of the art results on the SHREC17 tasks. The model places 2nd or 3rd in all categories but was not submitted as the SHREC17 task is closed. Table 2 shows the comparison of results with the top 3 submissions in each category. In the table, P@N stands for precision, R@N stands for recall, F1@N stands for F-score, mAP stands for mean average precision, and NDCG stands for normalized discounted cumulative gain in relevance based on whether the category and subcategory labels are predicted correctly. The authors claim the results show empirical proof of the usefulness of spherical CNNs. They elaborate that this is largely due to the fact that most architectures on the SHREC17 competition are highly specialized whereas their model is fairly general.
Molecular Atomization
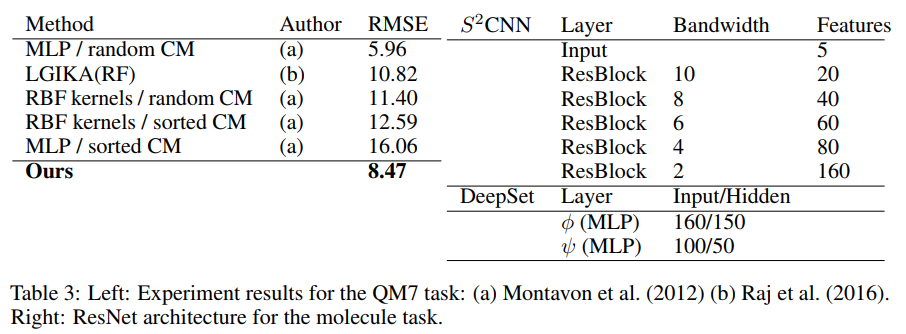
In this experiment a spherical CNN is implemented with an architecture resembling that of ResNet. They use the QM7 dataset (Blum et al. 2009) which has the task of predicting atomization energy of molecules. The QM7 dataset is a subset of GDB-13 (database of organic molecules) composed of all molecules up to 23 atoms. The positions and charges given in the dataset are projected onto the sphere using potential functions. For each atom, a sphere is defined around its position with the radius of the sphere kept uniform across all atoms. Next, the radius is chosen as the minimal radius so no intersections between atoms occur in the training set. Finally, using potential functions, a T channel spherical signal is produced for each atom in the molecule as shown in the figure below. A summary of their results is shown in Table 3 along with some of the spherical CNN architecture details. It shows the different RMSE obtained from different methods. The results from this final experiment also seem to be promising as the network the authors present achieves the second best score. They also note that the first place method grows exponentially with the number of atoms per molecule so is unlikely to scale well.

Conclusions
This paper presents a novel architecture called Spherical CNNs and evaluate it on 2 important learning problems and introduces a trainable signal representation for spherical signals rotationally equivariant by design. The paper defines [math]\displaystyle{ \small S^2 }[/math] and SO(3) cross correlations, shows the theory behind their rotational invariance for continuous functions, and demonstrates that the invariance also applies to the discrete case. An effective GFFT algorithm was implemented and evaluated on two very different datasets with close to state of the art results, demonstrating that there are practical applications to Spherical CNNs. The network is able to generalize across rotation and generate comparative results in the process.
For future work the authors believe that improvements can be obtained by generalizing the algorithms to the SE(3) group (SE(3) simply adds translations in 3D space to the SO(3) group). The authors also briefly mention their excitement for applying Spherical CNNs to omnidirectional vision such as in drones and autonomous cars. They state that there is very little publicly available omnidirectional image data which could be why they did not conduct any experiments in this area.
Commentary
The reviews on Spherical CNNs are very positive and it is ranked in the top 1% of papers submitted to ICLR 2018. Positive points are the novelty of the architecture, the wide variety of experiments performed, and the writing. One critique of the original submission is that the related works section only lists, instead of describing, previous methods and that a description of the methods would have provided more clarity. The authors have since expanded the section however I found that it is still limited which the authors attribute to length limitations. Another critique is that the evaluation does not provide enough depth. For example, it would have been great to see an example of omnidirectional vision for spherical networks. However, this is to be expected as it is just the introduction of spherical CNNs and more work is sure to come.
Source Code
Source code is available at: https://github.com/jonas-koehler/s2cnn
Sources
- T. Cohen et al. Spherical CNNs, 2018.
- J. Feldman. Haar Measure. http://www.math.ubc.ca/~feldman/m606/haar.pdf
- P. Kostelec, D. Rockmore. FFTs on the Rotation Group, 2008.