Searching For Efficient Multi Scale Architectures For Dense Image Prediction: Difference between revisions
| (5 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
=Introduction= | =Introduction= | ||
The design of neural network architectures is an important component for the success of machine learning and data science projects. In recent years, the field of Neural Architecture Search (NAS) has emerged, which is to automatically find an optimal neural architecture for a given task in a well-defined architecture space. The resulting architectures have often | The design of neural network architectures is an important component for the success of machine learning and data science projects. In recent years, the field of Neural Architecture Search (NAS) has emerged, which is to automatically find an optimal neural architecture for a given task in a well-defined architecture space. The resulting architectures have often outperformed networks designed by human experts on tasks such as image classification and natural language processing. [2,3,4] | ||
This paper presents a meta-learning technique to have computers search for a neural architecture that performs well on the task of dense image segmentation, mainly focused on the problem of scene labeling. | This paper presents a meta-learning technique to have computers search for a neural architecture that performs well on the task of dense image segmentation, mainly focused on the problem of scene labeling. | ||
| Line 11: | Line 11: | ||
The part of deep neural networks(DNN) success is largely due to the fact that it greatly reduces the work in feature engineering. This is because DNNs have the ability to extract useful features given the raw input. However, this creates a new paradigm to look at - network engineering. In order to extract significant features, an appropriate network architecture must be used. Hence, the engineering work is shifted from feature engineering to network architecture design for better abstraction of features. | The part of deep neural networks(DNN) success is largely due to the fact that it greatly reduces the work in feature engineering. This is because DNNs have the ability to extract useful features given the raw input. However, this creates a new paradigm to look at - network engineering. In order to extract significant features, an appropriate network architecture must be used. Hence, the engineering work is shifted from feature engineering to network architecture design for better abstraction of features. | ||
The motivation for NAS is to establish a guiding theory behind how to design | The motivation for NAS is to establish a guiding theory behind how to design optimal network architecture. Given that there is an | ||
abundant amount of computational resources available, an intuitive solution is to define a finite search space for a computer to search for optimal network structures and hyperparameters. | abundant amount of computational resources available, an intuitive solution is to define a finite search space for a computer to search for optimal network structures and hyperparameters. | ||
| Line 107: | Line 107: | ||
[[File:NAS_fig2.png|center|500px]] | [[File:NAS_fig2.png|center|500px]] | ||
Average spatial pyramid pooling | Average spatial pyramid pooling performs mean pooling on the last convolution layer (either convolution or sub sampling) and produces a N*B dimensional vector (where N=Number of filters in the convolution layer, B= Number of Bins). The vector is in turn fed to the fully connected layer. The number of bins is a constant value. Therefore, the vector dimension remains constant irrespective of the input image size. | ||
The resulting search space is able to encode all the main state-of-the-art architectures(i.e. Deformable Convnets [11], ASPP, Dense-ASPP [12] etc.), but these encoded architectures are more diverse since each branch of a DPC cell could build contextual information through parallel or cascaded representations. The number of potential architectures may determine the potential diversity of the search space. For <math display="inline">i</math>-th branch, there are <math display="inline">i</math> possible inputs, including the last feature maps produced by the network backbone, all the outputs from previous branch (<math display="inline">i.e., Y_1,...,Y_{i-1}</math>), and also 1 + 8×8 + 4×4 = 81 functions in the operator space, resulting in <math display="inline">i × 81</math> possible options. Therefore, for B = 5, the search space size is B! × 81^B ≈ 4.2 × 10^11 configurations. | The resulting search space is able to encode all the main state-of-the-art architectures(i.e. Deformable Convnets [11], ASPP, Dense-ASPP [12] etc.), but these encoded architectures are more diverse since each branch of a DPC cell could build contextual information through parallel or cascaded representations. The number of potential architectures may determine the potential diversity of the search space. For <math display="inline">i</math>-th branch, there are <math display="inline">i</math> possible inputs, including the last feature maps produced by the network backbone, all the outputs from previous branch (<math display="inline">i.e., Y_1,...,Y_{i-1}</math>), and also 1 + 8×8 + 4×4 = 81 functions in the operator space, resulting in <math display="inline">i × 81</math> possible options. Therefore, for B = 5, the search space size is B! × 81^B ≈ 4.2 × 10^11 configurations. | ||
[[File:picture2.png|center|500px]] | |||
=Search Strategy= | =Search Strategy= | ||
| Line 128: | Line 130: | ||
It essentially repeatedly searches randomly within the hypersphere of the current state, and updates only if the reward function is increased when using the newly found vector. The approach is highly non-parametric, and is easily generalized for complex problems such as architectural finding once parameters are properly defined. Although Random Search can return a reasonable approximation of the optimal solution under low problem dimensionality, the approach is commonly cited to perform poorly under higher problem dimensionality. The implementation of Random Search within this context is used to find highly complex architectures with millions of parameters; this could explain the only marginal improvements to human created state-of-the art networks despite the heavy machinery used to arrive at new architectures in the experiments section. | It essentially repeatedly searches randomly within the hypersphere of the current state, and updates only if the reward function is increased when using the newly found vector. The approach is highly non-parametric, and is easily generalized for complex problems such as architectural finding once parameters are properly defined. Although Random Search can return a reasonable approximation of the optimal solution under low problem dimensionality, the approach is commonly cited to perform poorly under higher problem dimensionality. The implementation of Random Search within this context is used to find highly complex architectures with millions of parameters; this could explain the only marginal improvements to human created state-of-the art networks despite the heavy machinery used to arrive at new architectures in the experiments section. | ||
They quoted from another paper that claims random search performs the random search is competitive with reinforcement learning and other learning techniques | They quoted from another paper that claims random search performs the random search is competitive with reinforcement learning and other learning techniques [7]. In the implementation, they used Google's black box optimization tool Google vizier. It is not open source, but there is an open source implementation of it [8]. A more recent and detailed survey detailing other methods such as Bayesian optimization strategies for Neural architecture search can be found in [13] | ||
In the implementation, they used Google's black box optimization tool Google vizier. It is not open source, but there is an open source implementation of it [8] | |||
=Performance Evaluation Strategy= | =Performance Evaluation Strategy= | ||
| Line 169: | Line 170: | ||
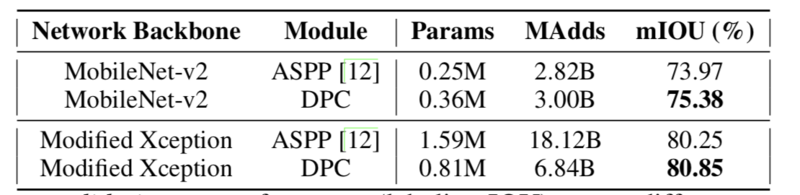
As we can see, the searched DPC model achieves better performance (measured by mIOU) with less than half of the computational resources(parameters), and 37% less of operations (add and multiply). | As we can see, the searched DPC model achieves better performance (measured by mIOU) with less than half of the computational resources(parameters), and 37% less of operations (add and multiply). | ||
=Conclusion= | |||
The paper demonstrates, how architecture search techniques can be employed for problems beyond image classification - in particular , problems of dense image prediction where multi-scale processing is critical for achieving state of the art performance. The paper focused on application of architecture search to dense image prediction through - 1.) Construction of recursive search space, leveraging innovations in the dense prediction literature and 2.) the construction of a fast proxy predictions of the large scale task. The resulting learned architecture surpasses human-invented architectures across three dense image prediction tasks: scene parsing , person-part segmentation and semantic segmentation. The authors also conclude that - The use of intelligent search algorithms such as reinforcement learning, sequential model-based optimization and evolutionary methods may be leveraged to further improve search efficiency particularly as the space grows in size. | |||
=Future work= | =Future work= | ||
| Line 224: | Line 229: | ||
12. M. Yang, K. Yu, C. Zhang, Z. Li, and K. Yang. Denseaspp for semantic segmentation in street scenes. In CVPR, 2018. | 12. M. Yang, K. Yu, C. Zhang, Z. Li, and K. Yang. Denseaspp for semantic segmentation in street scenes. In CVPR, 2018. | ||
13. Elsken, Thomas, Jan Hendrik Metzen, and Frank Hutter. "Neural architecture search: A survey." arXiv preprint arXiv:1808.05377 (2018). | |||
Latest revision as of 18:12, 14 December 2018
[Need add more pics and references]
Introduction
The design of neural network architectures is an important component for the success of machine learning and data science projects. In recent years, the field of Neural Architecture Search (NAS) has emerged, which is to automatically find an optimal neural architecture for a given task in a well-defined architecture space. The resulting architectures have often outperformed networks designed by human experts on tasks such as image classification and natural language processing. [2,3,4]
This paper presents a meta-learning technique to have computers search for a neural architecture that performs well on the task of dense image segmentation, mainly focused on the problem of scene labeling.
Motivation
The part of deep neural networks(DNN) success is largely due to the fact that it greatly reduces the work in feature engineering. This is because DNNs have the ability to extract useful features given the raw input. However, this creates a new paradigm to look at - network engineering. In order to extract significant features, an appropriate network architecture must be used. Hence, the engineering work is shifted from feature engineering to network architecture design for better abstraction of features.
The motivation for NAS is to establish a guiding theory behind how to design optimal network architecture. Given that there is an abundant amount of computational resources available, an intuitive solution is to define a finite search space for a computer to search for optimal network structures and hyperparameters.
Related Work
This paper focuses on two main literature research topics. One is the neural architecture search (NAS) and the other is the Multi-Scale representation for dense image prediction. Neural architecture search trains a controller network to generate neural architectures. The following are the important research directions in this area:
1) One kind of research transfers architectures learned on a proxy dataset to more challenging datasets and demonstrates superior performance over many human-invented architectures.
2) Reinforcement learning, evolutionary algorithms and sequential model-based optimization have been used to learn network structures.
3) Some other works focus on increasing model size, sharing model weights to accelerate model search or a continuous relaxation of the architecture representation.
4) Some recent methods focus on proposing methods for embedding an exponentially large number of architectures in a grid arrangement for semantic segmentation tasks.
In the area of multi-scale representation for dense image prediction the following are useful prior work:
1) State of the art methods use Convolutional Neural Nets. There are different methods proposed for supplying global features and context information to perform pixel level classification.
2) Some approaches focus on how to efficiently encode multi-scale context information in a network architecture like designing models that take an input an image pyramid so that large-scale objects are captured by the downsampled image.
3) Research also tried to come up with a theme on how best to tune the architecture to extract context information. Some works focus on sampling rates in atrous convolution to encode multi-scale context. Some others build context module by gradually increasing the rate on top of belief maps.
NAS Overview
NAS essentially turns a design problem into a search problem. As a search problem in general, we need a clear definition of three things:
- Search space
- Search strategy
- Performance Estimation Strategy
The search space is easy to understand, for instance defining a hyperparameter space to consider for our optimal solution. In the field of NAS, the search space is heavily dependent on the assumptions we make on the neural architecture. The search strategy details how to explore the search space. The evaluation strategy refers to taking an input of a set of hyperparameters, and from there evaluating how well our model fits. In the field of NAS, it is typical to find architectures that achieve high predictive performance on unseen data. [5]
We will take a deep dive into the above three dimensions of NAS in the following sections
Search Space
The purpose of architecture search space is to design a space that can express various state-of-the-art architectures, and able to identify good models.
There are typically three ways of defining the search space.
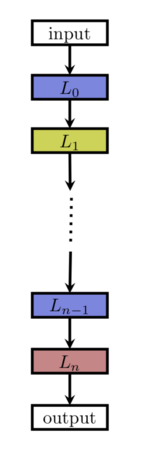
Chain-structured neural networks
[5] The chain structed network can be viewd as sequence of n layers, where the layer [math]\displaystyle{ i }[/math] recives input from [math]\displaystyle{ i-1 }[/math] layer and the output serves the input to layer [math]\displaystyle{ i+1 }[/math].
The search space is then parametrized by: 1) Number of layers n 2) Type of operations can be executed on each layer 3) Hyperparameters associated with each layer
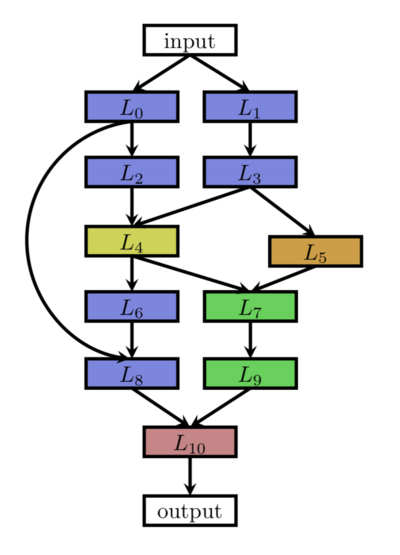
Multi-branch networks
[5] This architecture allows significantly more degrees of freedom. It allows shortcuts and parallel branches. Some of the ideas are inspired by human hand-crafted networks. For example, the shortcut from shallow layers directly to the deep layers are coming from networks like ResNet [6]
The search space includes the search space of chain-structured networks, with additional freedom of adding shortcut connections and allowing parallel branches to exist.
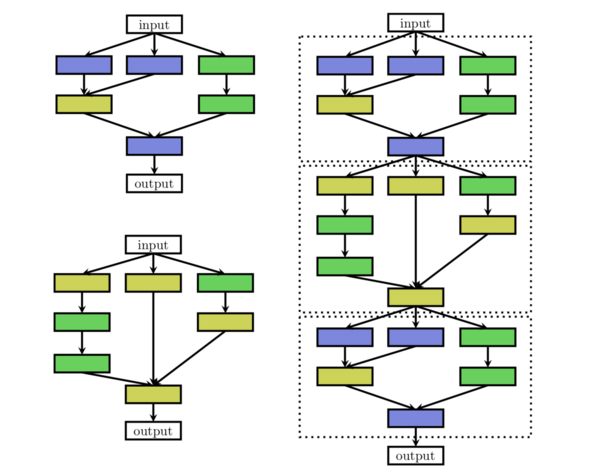
Cell/Block
[6] This architecture defines a cell which is used as the building block of the neural network. A good analogy here is to think a cell as a lego piece, and you can define different types of cells as different lego pieces. And then you can combine them together to form a new neural structure.
The search space includes the internal structure of the cell and how to combine these blocks to form the resulting architecture.
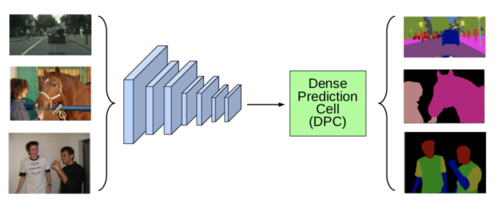
What they used in this paper
[1] This paper's approach is very close to the Cell/Block approach above
The paper defines two components: The "network backbone" and a cell unit called "DPC" which represented by a directed acyclic graph (DAG) with five branches (i.e. the optimal value, which gives a good balance between flexibility and computational tractability). A DAG is a finite directed graph with no directed cycles which consists of finitely many vertices and edges, with each edge directed from one vertex to another, such that there is no way to start at any vertex [math]\displaystyle{ v }[/math] and follow a consistently-directed sequence of edges that eventually loops back to [math]\displaystyle{ v }[/math] again. The network backbone's job is to take input image as a tensor and return a feature map f that is a supposedly good abstraction of the image. The DPC is what they introduced in this paper, short for Dense Prediction Cell, that is a recursive search space to encode multi-scale context information for dense prediction tasks. In theory, the search space consists of what they choose for the network backbone and the internal structure of the DPC. In practice, they just used MobileNet and Modified Xception net as the backbone. So the search space only consists of the internal structure of the DPC cell.
For the network backbone, they simply choose from existing mature architecture. They used networks like Mobile-Net-v2, Inception-Net, and e.t.c. For the structure of DPC, they define a smaller unit of called branch. A branch is a triple of (Xi, OP, Yi), where Xi is an input tensor, and OP is the operation that can be done on the tensor, and Yi is the resulting after the Operation.
In the paper, they set each DPC consists of 5 cells for the balance expressivity and computational tractability.
The operator space, OP, is defined as the following set of functions:
- Convolution with a 1 × 1 kernel.
- 3×3 atrous separable convolution with rate rh×rw, where rh and rw ∈ {1, 3, 6, 9, . . . , 21}.
- Average spatial pyramid pooling with grid size gh × gw, where gh and gw ∈ {1, 2, 4, 8}.
For the spatial pyramid pooling operation, average pooling is performed in each grid. After the average pooling, a 1×1 convolution is applied and the then the resize back the features to have the same spatial resolution as the input tensor.
Separable convolution with 256 filters is employed for all convolutions and 3x3 atrous convolutions with sampling rates rh x rw allows for capturing object scales with different aspect ratios. This is illustrated in the diagram below:

Average spatial pyramid pooling performs mean pooling on the last convolution layer (either convolution or sub sampling) and produces a N*B dimensional vector (where N=Number of filters in the convolution layer, B= Number of Bins). The vector is in turn fed to the fully connected layer. The number of bins is a constant value. Therefore, the vector dimension remains constant irrespective of the input image size.
The resulting search space is able to encode all the main state-of-the-art architectures(i.e. Deformable Convnets [11], ASPP, Dense-ASPP [12] etc.), but these encoded architectures are more diverse since each branch of a DPC cell could build contextual information through parallel or cascaded representations. The number of potential architectures may determine the potential diversity of the search space. For [math]\displaystyle{ i }[/math]-th branch, there are [math]\displaystyle{ i }[/math] possible inputs, including the last feature maps produced by the network backbone, all the outputs from previous branch ([math]\displaystyle{ i.e., Y_1,...,Y_{i-1} }[/math]), and also 1 + 8×8 + 4×4 = 81 functions in the operator space, resulting in [math]\displaystyle{ i × 81 }[/math] possible options. Therefore, for B = 5, the search space size is B! × 81^B ≈ 4.2 × 10^11 configurations.
Search Strategy
There are some common search strategies used in the field of NAS, such as Reinforcement learning, Random search, Evolution algorithm, and Grid Search.
The one they used in the paper is Random Search. It basically samples points from the search space uniformly at random as well as sampling some points that are close to the current observed best point. Intuitively it makes sense because it combines exploration and exploitation. When you sample points close to the current optimal point, you are doing exploitation. And when you sample points randomly, you are doing exploration.
The pseudocode for a general random search algorithm is provided below.
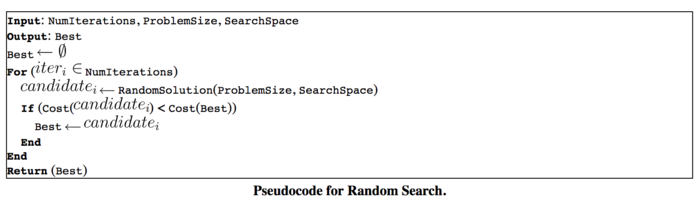
It essentially repeatedly searches randomly within the hypersphere of the current state, and updates only if the reward function is increased when using the newly found vector. The approach is highly non-parametric, and is easily generalized for complex problems such as architectural finding once parameters are properly defined. Although Random Search can return a reasonable approximation of the optimal solution under low problem dimensionality, the approach is commonly cited to perform poorly under higher problem dimensionality. The implementation of Random Search within this context is used to find highly complex architectures with millions of parameters; this could explain the only marginal improvements to human created state-of-the art networks despite the heavy machinery used to arrive at new architectures in the experiments section.
They quoted from another paper that claims random search performs the random search is competitive with reinforcement learning and other learning techniques [7]. In the implementation, they used Google's black box optimization tool Google vizier. It is not open source, but there is an open source implementation of it [8]. A more recent and detailed survey detailing other methods such as Bayesian optimization strategies for Neural architecture search can be found in [13]
Performance Evaluation Strategy
The evaluation in this particular task is very tricky. The reason is we are evaluating neural network here. In order to evaluate it, we need to train it first. And we are doing pixel level classification on images with high resolutions, so the naive approach would require a tremendous amount of computational resources.
The way they solve it in the paper is defining a proxy task. The proxy task is a task that requires sufficient less computational resources, while can still give a good estimate of the performance of the network. In most image classical tasks of NAS, the proxy task is to train the network on images of lower resolution. The assumption is, if the network performs well on images with lower density, it should reasonably perform well on images with higher resolution.
However, the above approach does not work on this case. The reason is that the dense prediction tasks innately require high-resolution images as training data. The approach used in the paper is the flowing:
- Use a smaller backbone for proxy task
- caching the feature maps produced by the network backbone on the training set and directly building a single DPC on top of it
- Early stopping train for 30k iterations with a batch size of 8
If training on the large-scale backbone without fixing the weights of the backbone, they would need one week to train a network on a P100 GPU, but now they cut down the proxy task to be run 90 min. Then they rank the selected architectures, choosing the top 50 and do a full evaluation on it.
The evaluation metric they used is called mIOU, which is pixel level intersection over union. Which just the area of the intersection of the ground truth and the prediction over the area of the union of the ground truth and the prediction.
Result
This method achieves state of art performances in many datasets. The following table quantifies the gain on performance on many datasets.
The chose to train on modified Xception network as a backbone, and the following are the resulting architecture for the DPC.
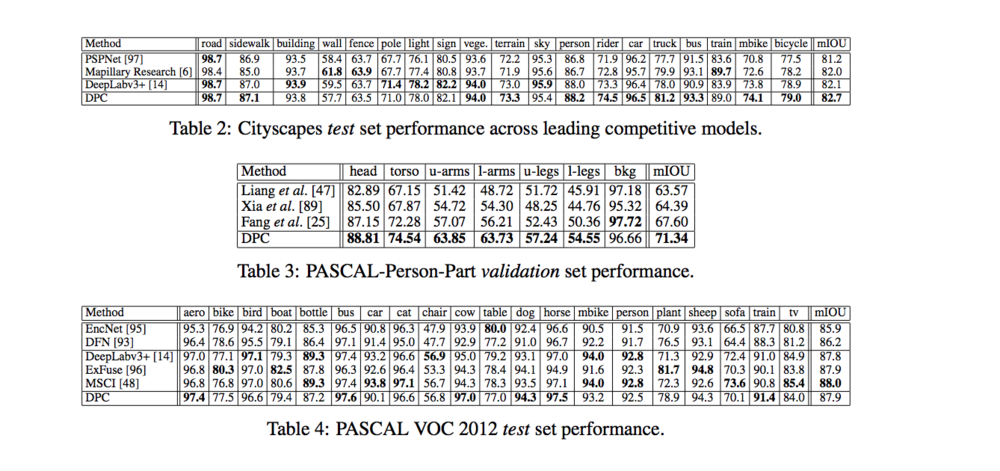
Table 2 describes the results on scene parsing dataset. It sets a new state-of-the-art performance of 82.7% mIOU and outperforms other state-of-the-art models across 11 of the 19 categories.
Table 3 describes the results on person part segmentation dataset. It achieve the state-of-the-art performance of 71.34% mIOU and outperforms other state-of-the-art models across 6 of the 7 categories.
Table 4 describes the results on semantic image segmentation dataset. It achieve the state-of-the-art performance of 87.9% mIOU and outperforms other state-of-the-art models across 6 of the 20 categories.
As we can see, the searched DPC model achieves better performance (measured by mIOU) with less than half of the computational resources(parameters), and 37% less of operations (add and multiply).
Conclusion
The paper demonstrates, how architecture search techniques can be employed for problems beyond image classification - in particular , problems of dense image prediction where multi-scale processing is critical for achieving state of the art performance. The paper focused on application of architecture search to dense image prediction through - 1.) Construction of recursive search space, leveraging innovations in the dense prediction literature and 2.) the construction of a fast proxy predictions of the large scale task. The resulting learned architecture surpasses human-invented architectures across three dense image prediction tasks: scene parsing , person-part segmentation and semantic segmentation. The authors also conclude that - The use of intelligent search algorithms such as reinforcement learning, sequential model-based optimization and evolutionary methods may be leveraged to further improve search efficiency particularly as the space grows in size.
Future work
The author suggests that when increasing the number of branches in the DPC, there might be a further gain on the performance on the image segmentation task. However, although the random search in an exponentially growing space may become more challenging. There may need more intelligent search strategy. They hope that by using some meta learning on metadata it can lead to future insight and be advantageous.
The author hope that this architecture search techniques can be ported into other domains such as depth prediction and object detection to achieve similar gains over human-invented designs.
Critique
1. Rich man's game
The technique described in the paper can only be applied by parties with abundant computational resources, like Google, Facebook, Microsoft, and e.t.c. For small research groups and companies, this method is not that useful due to the lack of computational power. Future improvement will be needed on the design an even more efficient proxy task that can tell whether a network will perform well that requires fewer computations.
2. Benefit/Cost ratio
The technique here does outperform human designed network in many cases, but the gain is not huge. In Cityscapes dataset, the performance gain is 0.7%, wherein PASCAL-Person-Part dataset, the gain is 3.7%, and the PASCAL VOC 2012 dataset, it does not outperform human experts. (All measured by mIOU) Even though the push of the state-of-the-art is always something that worth celebrating, but in practice, one would argue after spending so many resources doing the search, the computer should achieve superhuman performance. (Like Chess Engine vs Chess Grand Master). In practice, one may simply go with the current state-of-the-art model to avoid the expensive search cost.
3. Still Heavily influenced by Human Bias
When we define the search space, we introduced human bias. Firstly, the network backbone is chosen from previous matured architectures, which may not actually be optimal. Secondly, the internal branches in the DPC also consist with layers whose operations are defined by us humans, and we define these operations based on previous experience. That also prevents the search algorithm to find something revolutionary.
4. May have the potential to take away entry-level data science jobs.
If there is a significant reduction in the search cost, it will be more cost effective to apply NAS rather than hire data scientists. Once matured, this technology will have the potential to take away entry-level data science jobs and make data science jobs only possessed by high-level researchers.
There are some real-world applications that already deploy NAS techniques in production. Two good examples are Google AutoML and Microsoft Custom Vision AI. [9, 10]
References
1. Searching For Efficient Multi-Scale Architectures For Dense Image Prediction, [[1]].
2. E. Real, A. Aggarwal, Y. Huang, and Q. V. Le. Regularized evolution for image classifier architecture search. arXiv:1802.01548, 2018.
3. C. Liu, B. Zoph, M. Neumann, J. Shlens, W. Hua, L.-J. Li, L. Fei-Fei, A. Yuille, J. Huang, and K. Murphy. Progressive neural architecture search. In ECCV, 2018.
4. B. Zoph, V. Vasudevan, J. Shlens, and Q. V. Le. Learning transferable architectures for scalable image recognition. In CVPR, 2018.
5. Neural Architecture Search: A Survey [[2]]
6. Deep Residual Learning for Image Recognition [[3]]
7. J. Long, E. Shelhamer, and T. Darrell. Fully convolutional networks for semantic segmentation. In CVPR, 2015. In the implementation wise, they used a Google vizier, which is a search tool for black box optimization. [D. Golovin, B. Solnik, S. Moitra, G. Kochanski, J. Karro, and D. Sculley. Google vizier: A service for black-box optimization. In SIGKDD, 2017.]
8. Github implementation of Google Vizer, a black-box optimization tool [4]
9. AutoML: https://cloud.google.com/automl/
10. Custom-vision: https://azure.microsoft.com/en-us/services/cognitive-services/custom-vision-service/
11. J. Dai, H. Qi, Y. Xiong, Y. Li, G. Zhang, H. Hu, and Y. Wei. Deformable convolutional networks. In ICCV, 2017.
12. M. Yang, K. Yu, C. Zhang, Z. Li, and K. Yang. Denseaspp for semantic segmentation in street scenes. In CVPR, 2018.
13. Elsken, Thomas, Jan Hendrik Metzen, and Frank Hutter. "Neural architecture search: A survey." arXiv preprint arXiv:1808.05377 (2018).