STAT946F17/Decoding with Value Networks for Neural Machine Translation
Introduction
Background Knowledge
- NMT
Neural Machine Translation (NMT), which is based on deep neural networks and provides an end-to-end solution to machine translation, uses an RNN-based encoder-decoder architecture to model the entire translation process. Specifically, an NMT system first reads the source sentence using an encoder to build a "thought" vector, a sequence of numbers that represents the sentence meaning; a decoder, then, processes the "meaning" vector to emit a translation. (Figure 1)[1]

- Generalization: Sequence-to-Sequence(Seq2Seq) Model
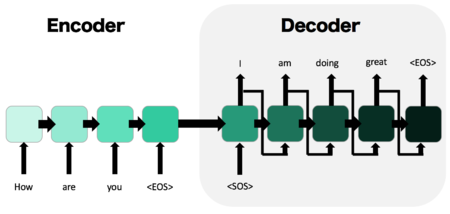
- Two RNNs: an encoder RNN, and a decoder RNN
- The input is passed through the encoder and it’s final hidden state, the “thought vector” is passed to the decoder as it’s initial hidden state.
- Decoder given the start of sequence token, <SOS>, and iteratively produces output until it outputs the end of sequence token, <EOS>
- Commonly used in text generation, machine translation, speech recognition and related problems
- Beam Search
Decoding process:
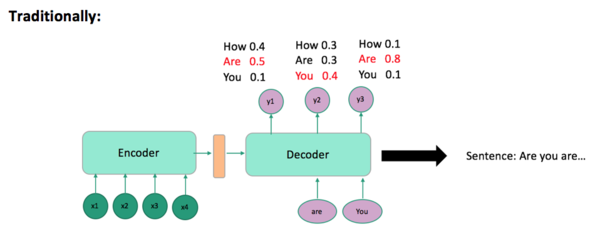
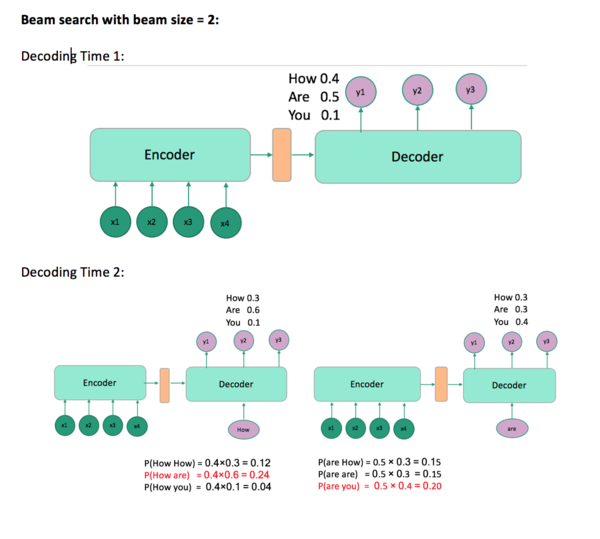
Problem: Choosing the word with the highest score at each time step t is not necessarily going to give you the sentence with the highest probability(Figure 3). Beam search solves this problem (Figure 4). Beam search is a heuristic search algorithm such that at each time step t, it takes the top m proposal and continues decoding with each one of them. In the end, you will get a sentence with the highest probability, not in the word level. The algorithm terminates if all sentences are completely generated, i.e., all sentences are ended with the <EOS> token.
value network
Upon the success of NMT with beam search, beam search tends to focus more on short-term reward, which is called myopic bias. At time t, a word $w$ may be appended to the candidates $y_{<t} = y_1,...,y_{t-1}$ if $P(y_{<t}+w|x) > P(y_{<t}+w'|x)$ even if the word $w'$ is the ground truth translation at step t or can offer a better score in future decodings. By applying the concept of value function in Reinforcement Learning (RL), the authors develop a neural network-based prediction model, the value network for NMT, to estimate the long-term reward when appending $w$ to $y_{<t}$ to address the myopic bias.
The value network takes the source sentence and any partial target sequence as input, and outputs a predicted value to estimate the expected total reward (e.g. BLEU[2]) so that select the best candidates in the decoding step is based on both conditional probability of the partial sequence outputted by the NMT model and the estimated long-term reward outputted by the value network.
Contributions
1) Developing a decoding scheme that considers long-term reward while generating words one by one for machine translation.
2) Building another two modules for the value network, a semantic matching module and a context-coverage module. The semantic matching module estimates the similarity between the source and target sentences. The context-coverage module measures the coverage of context used in the encoder-decoder layer observing the fact that better translation is generated when using more context in the attention mechanism.
Results of translation experiments demonstrate the effectiveness and robustness of the new decoding mechanism compared to several baseline algorithms.
Neural Machine Translation
NMT systems are implemented with a RNN based encoder-decoder framework, which directly models the probability $P(y|x)$ of a target sentence $y = {y_1,...,y_{T_y}}$ conditioned on the source sentence $x = {x_1,...,x_{T_x}}$, where $T_x$ and $T_y$ are the length of sentence x and y.
The encoder of NMT reads the source sentence x word by word and generates a hidden representation for each word xi: $$ h_i = f(h_{i-1},x_i) $$ where function f is the recurrent unit such as LSTM unit or GRU.
Then the decoder of NMT computes the conditional probability of each target word $y_t$ conditioned on its preceding words $y_{<t}$ and source sentence: $$ \begin{align*} c_t = q(r_{t-1};h_1,...,h_{T_x})\\ r_t = g(r_{t-1},y_{t-1},c_t)\\ P(y_t|y_{<t},x)\propto exp(y_t;r_t,c_t) \end{align*} $$ where,
$c_t$: weighted contextual information summarizing the source sentence x using some attention mechanism.
$r_t$: decoder RNN hidden representation at step t, computed by an LSTM or GRU
Notations:
- $Θ$: All learned parameters
- $π_{Θ}$: Translation model with parameter $Θ$
- D: training dataset that contains source-target sentence pairs.
The training process aims at seeking the optimal parameters $Θ^*$ using MLE to encode source sentence and decode it into the target sentence.
[math]\displaystyle{ Θ^* = \displaystyle\arg\max_{Θ} \prod\limits_{(x,y)∈D}P(y|x;Θ) = \displaystyle\arg\max_{Θ}\prod\limits_{(x,y)∈D}\prod\limits^{T_y}_{t=1}P(y_t|y_{\lt t},x;Θ) }[/math]
Value Network for NMT
Motivation: Beam search has limited ability at predicting a high-quality sentence due to myopic bias. [3][3] introduced scheduled sampling approach, which takes the generated outputs from the model and the golden truth sentence in training to help the model learn from its own errors but cannot avoid the myopic bias of beam search during testing. [4][4] learns a predictor to predict the ranking score of a certain word at step t, and use this score to replace the conditional probability outputted by the NMT model for beam search during testing. Unfortunately, this work still looks only one step forward and cannot address the problem. Thus the authors motivate to estimate the expected performance of any sequence during decoding based on the concept of value function in reinforcement learning.
Value Network Structure
In conventional reinforcement learning, a value function describes how much cumulated reward could be collected from state s by following certain policy $π$. In NMT, consider $x$ and $y_{<t}$ as the state, $π_{Θ}$ as policy which can generate a word (action) given any state. The value function characterizes the expected translation performance (e.g. BLEU score) when using $π_{Θ}$ to translate $x$ with the previous $t-1$ words, $y_{<t}$. The value function is defined as:
[math]\displaystyle{ v(x,y_{\lt t}) = \sum\limits_{y'∈Y: y'_{\lt t}=y_{\lt t}}BLEU(y^*(x),y')P(y'|x;Θ) }[/math]
where $y^*(x)$: ground truth translation, $Y$: the space of complete sentence.
Two modules are developed to fully exploit the information in the encoder-decoder framework.
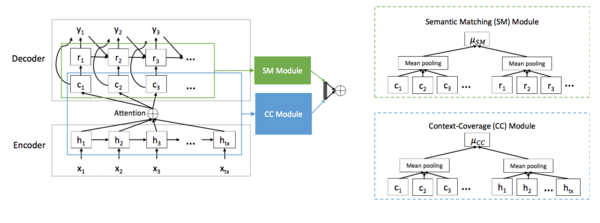
Semantic Matching (SM) Module: at time step, use mean pooling over the decoder RNN hidden states and the over the context states as summarizations of the partial target sequence and the context in source language. Then use a feed-forward network to evaluate semantic information between the source sentence and the target sentence. i.e.,
- $\bar{r_{t}} = \frac{1}{t}\sum\limits^{t}_{l=1}r_l$, $\bar{c_{t}} = \frac{1}{t}\sum\limits^{t}_{l=1}c_l$
- $𝜇_{SM} = f_{SM}([\bar{r_{t}},\bar{c_{t}}])$
Context-Coverage (CC) Module: It is often observed that more context covered in the attention model leads to better translation. CC is built to measure coverage of information in the network. Similarly as the process in SM module, the process is defined as:
- $\bar{h} = \frac{1}{T_x}\sum\limits^{T_x}_{l=1}h_l$
- $𝜇_{CC} = f_{CC}([\bar{c_{t}},\bar{h}])$
In the end, the authors concatenate $𝜇_{SM}$ and $𝜇_{CC}$ and then use another fully connected layer with sigmoid activation function to output a scalar as the value prediction. (Figure 5)
Training and Learning
The authors adopt the Monte-Carlo method to learn the value function. The training of the value network for NMT model $π_{Θ}$ is shown in Algorithm 1.

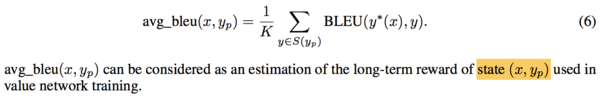
In conventional Monte-Carlo method for value function estimation, people usually use a regression model to approximate the value function, i.e., learn a mapping from $(x, y_p) \rightarrow avg\_bleu(x, y_p)$ by minimizing the mean square error (MSE). In this paper, the authors take an alternative objective function which is shown to be more effective in experiments.
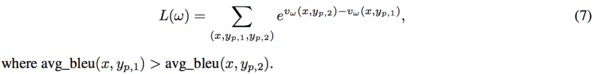
Notes:
- 4-8 for training; 9 for learning
- 9: Eqn.(7), for value function estimation, the authors minimize the pairwise ranking loss objective function to learn the mapping from $(x,y_p)$ → avg_bleu$(x,y_p)$ since they hope the value network to be useful in differentiating good and bad examples.
- 11: $w$ is the learned weights of the value network
Decoding Process
The authors linearly combine the conditional probability $P(y|x)$, which is the output of the NMT model and the value network representing the future reward motivated by the success of AlphaGo[5] They believe it would generate a better result by considering both past and future information. Mathematically,given a translation model $P(y|x)$, a value network $v(x,y)$ and a hyperparameter $𝛼∈(0,1)$, the score of partial sequence y for x is:
$𝛼×\frac{1}{|y|}\,log\,P(y|x) + (1-𝛼)×log\,v(x,y)$
where $|y|$ is the length of y. The details of the decoding process are presented in Algorithm 2. This neural network based decoding algorithm is called NMT-VNN for short.

Notes:
- If $𝛼=1$, it is just the original beam search algorithm (i.e., without considering the value network)
- $U_{complete}$: How many sentences are complete (reach the <EOS> token) at time step t.
- $S$: All full sentences found by beam search from time step 1 up to time step t.
Experiments
Settings
The author compare their proposed NMT-VNN with two baseline models, the classic NMT with beam search (NMT-BS)[6] and the one referred as beam search optimization (NMT-BSO), which trains a predictor to evaluate the quality of any partial sequence, and then uses the predictor to select words instead of the probability. Note the difference between NMT-BSO and their NMT-VNN is NMT-BSO predicts the local improvement of BLEU for any single word, while NMT-VNN predicts the final BLEU score and use the predicted score to select words.
The models are tested using three pairs of languages: English→French (En→Fr), English→German (En→De), and Chinese→English (Zh→En). They used the same bilingual corpora from WMT’14 as used in [6] , which contains 12M, 4.5M and 10M training data for each task.[6]
- For En→Fr and En→De: validation set: newstest2012 and newstest2013; test set: newstest2014
- For Zh→En: validation set: NIST 2004; test set: NIST 2006 and NIST 2008
For all datasets in Chinese, they use a public tool for Chinese word segmentation. In all experiments, validation sets were only used for early-stopping and hyperparameter tuning.
For NMT-VNN and NMT-BS, they first set experimental parameters to train an NMT model following [6]. The vocabulary for each language is the most common 30K in the parallel corpora and the words not in the vocabulary (i.e., unknown words) were replaced with a special token “UNK". Each word was embedded into a vector space of 620 dimensions, and recurrent unit has dimension of 1000. Sentences with length ≤ 50 were kept in the training set. Batch size was set as 80 with 20 batches pre-fetched and sorted by sentence lengths.
The NMT model was trained with asynchronized SGD on four K40m GPUs for about seven days. For NMT-BSO, they implemented the algorithm and the model was trained in the same environment. For the value network used in NMT-VNN, they set the same parameters for the encoder-decoder layers as the NMT model. Additionally, in the SM module and CC module, they set function $μ_{SM}$ and $μ_{CC}$ as single-layer feed forward networks with 1000 output nodes. In Algorithm 1, they set the hyperparameter K = 20 to estimate the value of any partial sequence. They used mini-batch training with batch size 80, and the value network model was trained with AdaDelta [8] on one K40m GPU for about three days.
During testing, the hyperparameter $𝛼$ for NMT-VNN was set by cross validation and they found the optimal $𝛼$ for En→Fr, En→De and Zh→En are 0.85, 0.9 and 0.8 respectively. They used the BLEU score [9] as the evaluation metric, which is computed by the multi-bleu.perl[10]. Beam search size was set to be 12 for all the algorithms following the common practice [11].
Results
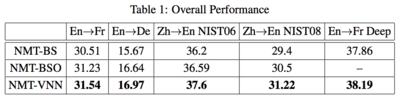
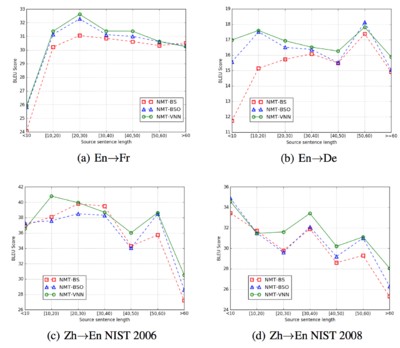
Table 1 shows that the NMT-VNN algorithm outperforms the baseline algorithms on all tasks, especially for harder level translations (Zh→En).
For En→Fr and En→De tasks, NMT-VNN outperforms NMT-BS by 1.03/1.3 points due to the additional use of value network, which suggests the additional knowledge provides useful information to help the NMT model. NMT-VNN outperforms NMT-BSO by about 0.31/0.33 points since NMT-BSO only uses a local BLEU predictor to estimate the partial BLEU score while NMT-VNN predicts the future performance, which shows the advantage of considering long-term rewards. For Zh→En task, NMT-VNN outperforms NMT-BS by 1.4/1.82 points on NIST 2006 and NIST 2008, and outperforms NMT-BSO by 1.01/0.72 points.
The plots BLEU Score vs. Source Sentence Length (Figure 6) depict NMT-VNN algorithm outperforms the baseline algorithms for almost any sentence length.
Furthermore, they also test the value network on a deep NMT model in which the encoder and decoder both have 4-layer LSTMs. The result (Table 1) shows 0.33 points improvement on the En→Fr task. These results demonstrate the effectiveness and robustness of the NMT-VNN algorithm.
Analysis on Value Network
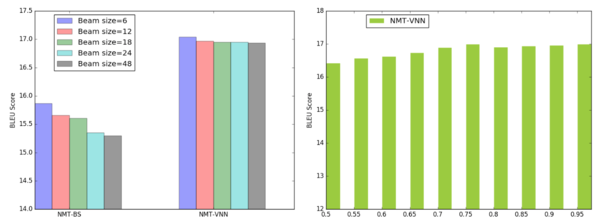
First, the additional component in decoding will affect the translation process.
Second, the accuracy of NMT sometimes drops dramatically as the beam size grows on certain tasks because the training of NMT favors short but inadequate translation candidates[12]. This happens for the En→De translation, however, such shortage can be largely avoided by using value network. Figure 7(a) shows the accuracy (BLEU score) using different beam size for the NMT-BS and the NMT-VNN models. NMT-VNN is much more stable than the original NMT as its accuracy only differs a little for different beam sizes while NMT-BS drops more than 0.5 points when the beam size is large.
Third, the performances of NMT-VNN using different hyperparameter 𝛼 during decoding for En→De task is shown in Figure 7(b) and it is stable for 𝛼 ranging from 0.7 to 0.95, and slightly drops for a smaller 𝛼. The authors declare the proposed algorithm is robust to the hyperparameter.
Conclusions and Future Work
This paper introduces a new decoding scheme that incorporates value networks for NMT. The new decoding scheme considers not only the local conditional probability of a candidate word but also its long-term reward for future decoding. Experiments on three translation tasks verify the effectiveness of the new scheme. For future works:
- designing better structures for the value network.
- extending it to other sequence-to-sequence learning tasks, such as image captioning and dialog systems.
Critiques
- It is a good idea to consider future reward by using the value network in addition to beam search which is based on past information. Intuitively, the NMT-VNN should improve the NMT by using both past and future information.
- The paper does not give much information or give any quantitative evaluations about the two modules they built, for example, how much the two modules contribute to the accuracy of their NMT-VNN model?
- In algorithm 1 step 5, it is reasonable to generate partial target sentence $y_{p,1}$,$y_{p,2}$ using $π_{Θ}$ with random early stop, but if the stop times for the two sentences are too far from each other, there could be a problem for the beam search...since beam size is kind of related to the number of words of the sentence left to generate.
- In the experiment results section, they only test the value network on a deep NMT model on the En→Fr task and show the improvement, is that true for all other translations?
- In the decoder section of the network, the authors could have experimented with fast-forward linear connections while stacking LSTMs. This technique has proven to obtain some of the best empirical accuracies in machine translation ( En->Fr BLEU= 37.7) [13].
References
[1] https://github.com/tensorflow/nmt
[2] https://en.wikipedia.org/wiki/BLEU
[3] S. Bengio, O. Vinyals, N. Jaitly, and N. Shazeer. Scheduled sampling for sequence prediction with recurrent neural networks. In Advances in Neural Information Processing Systems, pages 1171–1179, 2015.
[4] S. Wiseman and A. M. Rush. Sequence-to-sequence learning as beam-search optimization. In EMNLP, 2016.
[5] D. Silver, A. Huang, C. J. Maddison, A. Guez, L. Sifre, G. Van Den Driessche, J. Schrittwieser, I. Antonoglou, V. Panneershelvam, M. Lanctot, et al. Mastering the game of go with deep neural networks and tree search. Nature, 529(7587):484–489, 2016.
[6] D. Bahdanau, K. Cho, and Y. Bengio. Neural machine translation by jointly learning to align and translate. ICLR, 2015.
[8] M. D. Zeiler. Adadelta: an adaptive learning rate method. arXiv preprint arXiv:1212.5701, 2012.
[9] K. Papineni, S. Roukos, T. Ward, and W.-J. Zhu. Bleu: a method for automatic evaluation of machine translation. In Proceedings of the 40th annual meeting on association for computational linguistics, pages 311–318. Association for Computational Linguistics, 2002.
[10] https://github.com/moses-smt/mosesdecoder/blob/master/scripts/generic/multi-bleu.perl.
[11] I. Sutskever, O. Vinyals, and Q. V. Le. Sequence to sequence learning with neural networks. In Advances in neural information processing systems, pages 3104–3112, 2014.
[12] Z. Tu, Y. Liu, L. Shang, X. Liu, and H. Li. Neural machine translation with reconstruction. In AAAI, pages 3097–3103, 2017.
[13] Jie Zhou, Ying Cao, Xuguang Wang, Peng Li, Wei Xu ; "Deep Recurrent Models with Fast-Forward Connections for Neural Machine Translation". arXiv:1606.04199 [cs.CL]