STAT946F17/Conditional Image Generation with PixelCNN Decoders: Difference between revisions
No edit summary |
|||
| Line 81: | Line 81: | ||
$$y = tanh(W_{k,f} \ast x + V_{k,f} \ast s) \odot \sigma(W_{k,g} \ast x + V_{k,g} \ast s)$$ | $$y = tanh(W_{k,f} \ast x + V_{k,f} \ast s) \odot \sigma(W_{k,g} \ast x + V_{k,g} \ast s)$$ | ||
where $V_{k,g}\ | where $V_{k,g}\ast s$ is an unmasked $1\times1$ convolution. | ||
=PixelCNN Auto-Encoders= | =PixelCNN Auto-Encoders= | ||
Revision as of 15:07, 18 November 2017
NOT DONE YET!
Introduction
This works is based of the widely used PixelCNN and PixelRNN, introduced by Oord et al. in [1]. From the previous work, the authors observed that PixelRNN performed better than PixelCNN, however, PixelCNN was faster to compute as you can parallize the training process. In this work, Oord et al. [2] introduced a Gated PixelCNN, which is a convolutional variant of the PixelRNN model, based on PixelCNN. In particular, the Gated PixelCNN uses explicit probability densities to generate new images using autoregressive connections to model images through pixel-by-pixel computation by decomposing the joint image distribution as a product of conditionals. The Gated PixelCNN is an improvement over the PixelCNN by removing the "blindspot" problem, and to yield a better performance, the authors replaced the ReLU units with sigmoid and tanh activation function. The proposed Gated PixelCNN combines the strength of both PixelRNN and PixelCNN - that is by matching the log-likelihood of PixelRNN on both CIFAR and ImageNet along with the quicker computational time presented by the PixelCNN. Moreover, the authors also introduced a conditional Gated PixelCNN variant (called Conditional PixelCNN) which has the ability to generate images based on class labels, tags, as well as latent embeddings to create new image density models. These embeddings capture high level information of an image to generate a large variety of images with similar features; for instance, the authors can generate different poses of a person based on a single image by conditioning on a one-hot encoding of the class. This approach provided insight into the invariances of the embeddings which enabled the authors to generate different poses of the same person based on a single image. Finally, the authors also presented a PixelCNN Auto-encoder variant which essentially replaces the deconvolutional decoder with the PixelCNN.
Gated PixelCNN
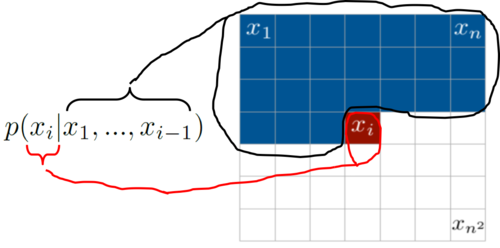
Pixel-by-pixel is a simple generative method wherein given an image of dimension of dimension $x_{n^2}$, we iterate, employ feedback and capture pixel densities from every pixel to predict our "unknown" pixel density $x_i$. To do this, the traditional PixelCNNs and PixelRNNs adopted the joint distribution p(x), wherein the pixels of a given image is the product of the conditional distributions. Hence, the authors employ autoregressive models which means they just use plain chain rule for joint distribution, depicted in Equation 1. So the very first pixel is independent, second depend on first, third depends on first and second and so on. Basically you just model your image as sequence of points where each pixel depends linearly on previous ones. Equation 1 depicts the joint distribution where x_i is a single pixel:
$$p(x) = \prod\limits_{i=1}^{n^2} p(x_i | x_1, ..., x_{i-1})$$
where $p(x)$ is the generated image, $n^2$ is the number of pixels, and $p(x_i | x_1, ..., x_{i-1})$ is the probability of the $i$th pixel which depends on the values of all previous pixels. It is important to note that $p(x_0, x_1, ..., x_{n^2})$ is the joint probability based on the chain rule - which is a product of all conditional distributions $p(x_0) \times p(x_1|x_0) \times p(x_2|x_1, x_0)$ and so on. Figure 1 provides a pictorial understanding of the joint distribution which displays that the pixels are computed pixel-by-pixel for every row, and the forthcoming pixel depends on the pixels values above and to the left of the pixel in concern.
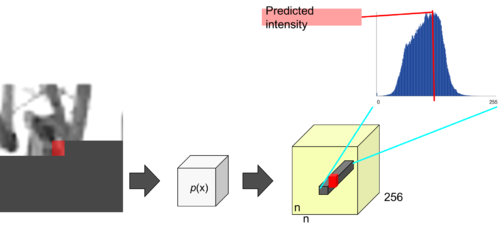
Hence, for every pixel, we use the softmax layer towards the end of the PixelCNN to predict the pixel intensity value (i.e. the highest probable index from 0 to 255). Figure 2 illustrates how to predict (generate) a single pixel value.
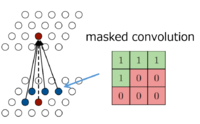
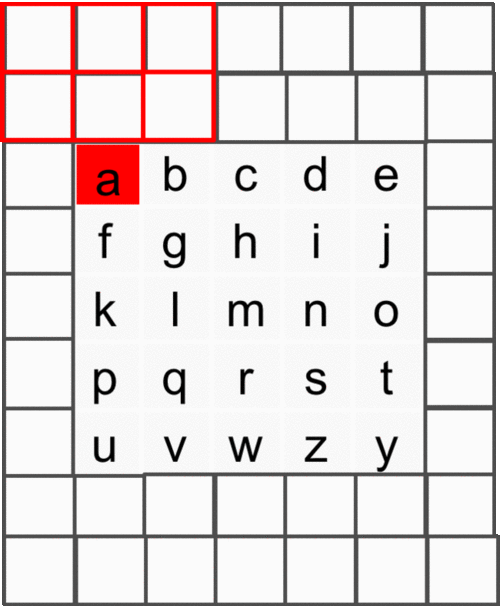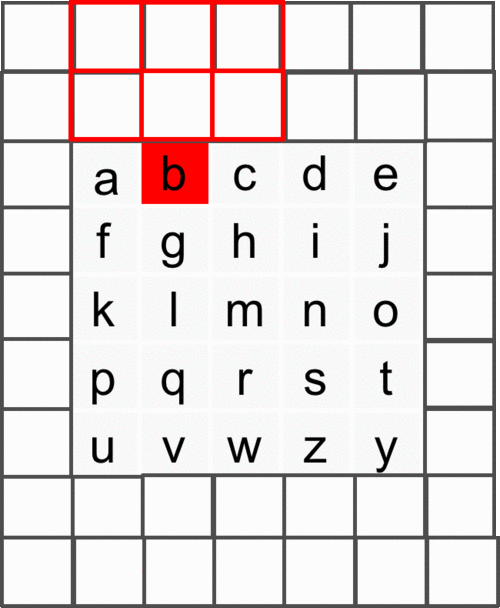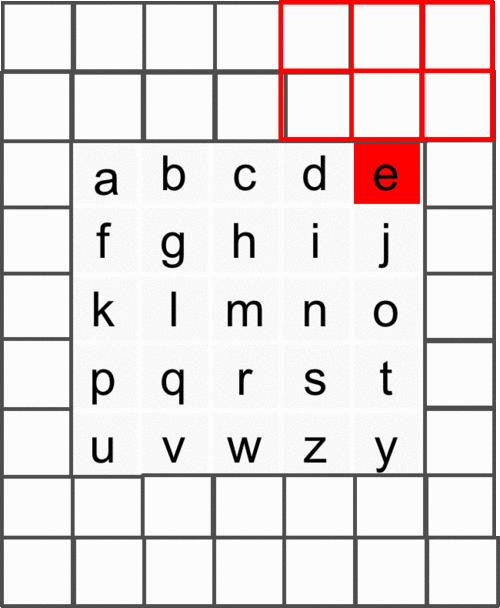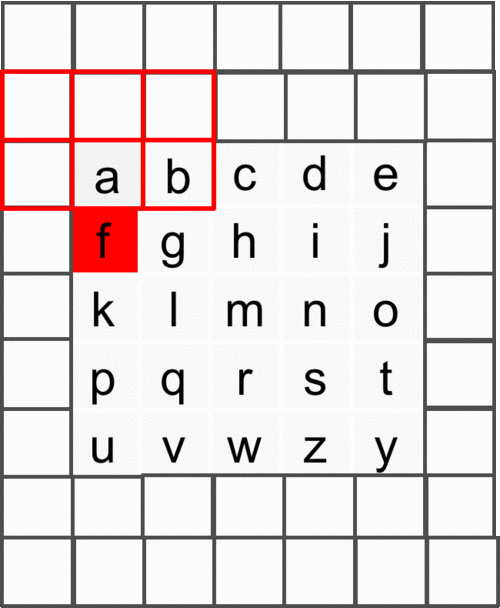
So, the PixelCNN is supposedly to maps a neighborhood of pixels to prediction for the next pixel. That is, to generate pixel $x_i$ the model can only condition on the previously generated pixels $x_1 , ..., x_{i−1}$; so every conditional distribution is modelled by a convolutional neural network. For instance, given a $5\times5$ image (let's represent each pixel as an alphabet and zero-padded), and we have a filter of dimension $3\times3$ that slides over the image which multiplies each element and sums them together to produce a single response. However, we cannot use this filter because pixel $a$ should not know the pixel intensities for $b,f,g$ (future pixel values). To counter this issue, the authors use a mask on top of the filter to only choose prior pixels and zeroing the future pixels to negate them from calculation - depicted in Figure 3. Hence, to make sure the CNN can only use information about pixels above and to the left of the current pixel, the filters of the convolution are masked - that means the model cannot read pixels below (or strictly to the right) of the current pixel to make its predictions.
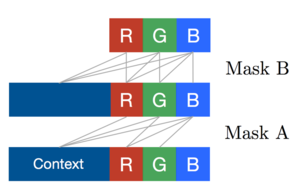
Hence, for each pixel there are three colour channels (R, G, B) which are modelled successively, with B conditioned on (R, G), and G conditioned on R. This is achieved by splitting the feature maps at every layer of the network into three and adjusting the centre values of the mask tensors, as depicted in Figure 4. The 256 possible values for each colour channel are then modelled using a softmax.
Now, from Figure 5, notice that as the filter with the mask slides across the image, pixel $f$ does not take pixels $c, d, e$ into consideration (breaking the conditional dependency) - this is where we encounter the "blind spot" problem.

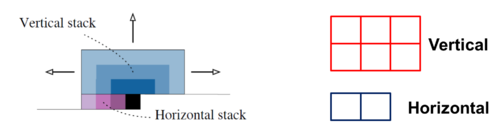
It is evident that the progressive growth of the receptive field of the masked kernel over the image disregards a significant portion of the image. For instance, when using a 3x3 filter, roughly quarter of the receptive field is covered by the "blind spot", meaning that the pixel contents are ignored in that region. In order to address the blind spot, the authors use two filters (horizontal and vertical stacks) in conjunction to allow for capturing the whole receptive field, depicted in Figure{vh_stack}. In particular, the horizontal stack conditions the current row, and the vertical stack conditions all the rows above the current pixel. It is observed that the vertical stack, which does not have any masking, allows the receptive field to grow in a rectangular fashion without any blind spot. Thereafter, the outputs of both the stacks, per-layer, is combined to form the output. Hence, every layer in the horizontal stack takes an input which is the output of the previous layer as well as that of the vertical stack. By spliting the convolution into two different operations enables the model to access all pixels prior to the pixel of interest.
Horizontal Stack
For the horizontal stack (in purple for Figure 7), the convolution operation conditions only on the current row, so it has access to left pixels. In essence, we take a $1 \times n//2+1$ convolution with shift (pad and crop) rather than $1\times n$ masked convolution. So, we perform convolution on the row with a kernel of width 2 pixels (instead of 3) from which the output is padded and cropped such that the image shape stays the same. Hence, the image convolves with kernel width of 2 and without masks.
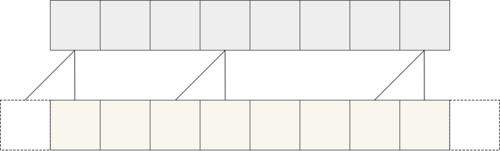
Figure 8 shows that the last pixel from output (just before ‘Crop here’ line) does not hold information from last input sample (which is the dashed line).
Vertical Stack
Vertical stack (blue) has access to all top pixels. The vertical stack is of kernel size $n//2 + 1 \times n$ with the input image being padded with another row in the top and bottom. Thereafter, we perform the convolution operation, and crop the image to force the predicted pixel to be dependent on the upper pixels only (i.e. to preserve the spatial dimensions). Since the vertical filter does not contain any "future" pixel values, only upper pixel values, no masking is incorporated as no target pixel is touched. However, the computed pixel from the vertical stack yields information from top pixels and sends that info to horizontal stack (which supposedly eliminates the "blindspot problem").
From Figure 9 it is evident that the image is padded (left) with kernel height zeros, then convolution operation is performed from which we crop the output so that rows are shifted by one with respect to input image. Hence, it is noticeable that the first row of output does not depend on first (real, non-padded) input row. Also, the second row of output only depends on the first input row - which is the desired behaviour.
Gated block
The PixelRNNs are observed to perform better than the traditional PixelCNN for generating new images. This is because the spatial LSTM layers in the PixelRNN allows for every layer in the network to access the entire neighbourhood of previous pixels. The PixelCNN, however, only takes into consideration the neighborhood region and the depth of the convolution layers to make its predictions. Another advantage for the PixelRNN is that this network contains multiplicative units (in the form of the LSTM gates), which may help it to model more complex interactions. To address the benefits of PixelRNN and append it onto the newly proposed Gated PixelCNN, the authors replaced the rectified linear units between the masked convolutions with the following custom-made gated activation function, depicted in Equation 2:
$$y = tanh(W_{k,f} \ast x) \odot \sigma(W_{k,g} \ast x)$$
where $\sigma$ is the sigmoid non-linearity, $k$ is the number of the layer, $f, g$ are the different feature maps, $\odot$ is the element-wise product and $\ast$ is the convolution with the input. This function is the key ingredient that cultivates the Gated PixelCNN model.
Figure 10 provides a pictorial illustration of a single layer in the Gated PixelCNN architecture; wherein the vertical stack contributes to the horizontal stack with the $1\times1$ convolution - going the other way would break the conditional distribution. In other words, the horizontal and vertical stacks are sort of independent, wherein vertical stack should not access any information horizontal stack has - otherwise it will have access to pixels it shouldn’t see. However, vertical stack can be connected to vertical as it predicts pixel following those in vertical stack. In particular, the convolution operations are shown in green (which are masked), element-wise multiplications and additions are shown in red. The convolutions with $W_f$ and $W_g$ are not combined into a single operation (which is essentially the masked convolution) to increase parallelization shown in blue. The parallelization now splits the $2p$ features maps into two groups of $p$. Finally, the authors also use the residual connection in the horizontal stack. Moreover, the $(n \times 1)$ and $(n \times n)$ are the masked convolutions which can also be implemented as $([n/2] \times 1)$ and $([n/2] \times n)$ which are convolutions followed by a shift in pixels by padding and cropping to get the original dimension of the image.
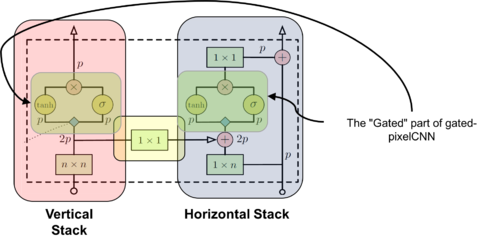
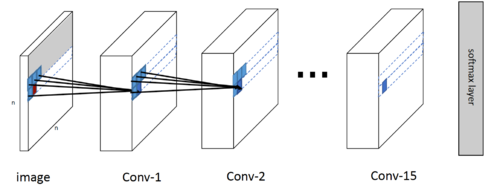
In essence, PixelCNN typically consists of a stack of masked convolutional layers that takes an $N \times N \times 3$ image as input and produces $N \times N \times 3 \times 256$ (probability of pixel intensity) predictions as output. During sampling the predictions are sequential: every time a pixel is predicted, it is fed back into the network to predict the next pixel. This sequentiality is essential to generating high quality images, as it allows every pixel to depend in a highly non-linear and multimodal way on the previous pixels.
Another important mention is that the residual connections are only for horizontal stacks. On the other side skip connections allow as to incorporate features from all layers at the very end of out network. Most important stuff to mention here is that skip and residual connection use different weights after gated block.
Conditional PixelCNN
Conditioning is a smart word for saying that we’re feeding the network some high-level information - for instance, providing an image to the network with the associated classes in MNIST/CIFAR datasets. During training you feed image as well as class to your network to make sure network would learn to incorporate that information as well. During inference you can specify what class your output image should belong to. You can pass any information you want with conditioning, we’ll start with just classes.
For a conditional PixelCNN, we represent a provided high-level image description as a latent vector $h$, wherein the purpose of the latent vector is to model the conditional distribution $p(x|h)$ such that we get a probability as to if the images suites this description. The conditional PixelCNN models based on the following distribution:
$$p(x|h) = \prod\limits_{i=1}^{n^2} p(x_i | x_1, ..., x_{i-1}, h)$$
Hence, now the conditional distribution is dependent on the latent vector h, which is now appended onto the activations prior to the non-linearities; hence the activation function after adding the latent vector becomes:
$$y = tanh(W_{k,f} \ast x + V_{k,f}^T h) \odot \sigma(W_{k,g} \ast x + V_{k,g}^T h)$$
Note $h$ multiplied by matrix inside tanh and sigmoid functions, $V$ matrix has the shape $[number of classes, number of filters]$, $k$ is the layer number, and the classes were passed as a one-hot vector $h$ during training and inference.
Note that if the latent vector h is a one-hot encoding vector that provides the class labels, which is equivalent to the adding a class dependent bias at every layer. So, this means that the conditioning is independent from the location of the pixel - this is only if the latent vector holds information about “what should the image contain” rather than the location of contents in the image. For instance, we could specify that a certain animal or object should appear in different positions, poses and backgrounds.
In addition, the authors also developed a variant that makes the conditional distribution dependent on the location (an application when the location of an object is important). This is achieved by mapping the latent vector $h$ to a spatial representation $s=m(h)$ (which contains the same dimension of the image but may have an arbitrary number of feature maps) with a deconvolutional neural network $m()$; this provides a location dependent bias as follows:
$$y = tanh(W_{k,f} \ast x + V_{k,f} \ast s) \odot \sigma(W_{k,g} \ast x + V_{k,g} \ast s)$$
where $V_{k,g}\ast s$ is an unmasked $1\times1$ convolution.
PixelCNN Auto-Encoders
Since conditional PixelCNNs can model images based on the distribution $p(x|h)$, it is possible to apply this analogy into image decoders used in Autoencoders. Introduced by Hinton et. al in [3], autoencoder is a dimensionality reduction neural network which is composed of two parts: an encoder which maps the input image into low-dimensional representation (i.e. the latent vector $h$) , and a decoder that decompresses the latent vector to reconstruct the original image.
In order to apply the conditional PixelCNN onto the autoencoder, the deconvolutional decoders are replaced with the conditional PixelCNN - the re-architectured network of which is used for training a data set. The authors observe that the encoder can better extract representations of the provided input data - this is because much of the low-level pixel statistics is now handled by the PixelCNN; hence, the encoder omits low-level pixel statistics and focuses on more high-level abstract information.
Summary
$\bullet$ Improved PixelCNN
- Similar performance as PixelRNN, and quick to compute like PixelCNN (since it is easier to parallelize)
- Fixed the "blind spot" problem by introducing 2 stacks (horizontal and vertical)
- Gated activation units which now use sigmoid and tanh instead of ReLU units
$\bullet$ Conditioned Image Generation
- One-shot conditioned on class-label
- Conditioned on portrait embedding
- Pixel AutoEncoders
Reference
- Aaron van den Oord et al., "Pixel Recurrent Neural Network", ICML 2016
- Aaron van den Oord et al., "Conditional Image Generation with PixelCNN Decoders", NIPS 2016