Robust Imitation of Diverse Behaviors
Introduction
One of the longest standing challenges in AI is building versatile embodied agents, both in the form of real robots and animated avatars, capable of a wide and diverse set of behaviors. State-of-the-art robots cannot compete with the effortless variety and adaptive flexibility of motor behaviors produced by toddlers. Towards addressing this challenge, the authors combine several deep generative approaches to imitation learning in a way that accentuates their individual strengths and addresses their limitations. The end product is a robust neural network policy that can imitate a large and diverse set of behaviors using few training demonstrations.
Motivation
Some of the models that have recently shown great promise in imitation learning for motor control are the deep generative models. The authors primarily talk about two approaches viz. supervised approaches that condition on demonstrations and Generative Adversarial Imitation Learning (GAIL) and their limitations and try to combine those two approaches in order to address these limitations. Some of these limitations are as follows:
- Supervised approaches that condition on demonstrations (VAE):
- They require large training datasets in order to work for non-trivial tasks
- They tend to be brittle and fail when the agent diverges too much from the demonstration trajectories
- Generative Adversarial Imitation Learning (GAIL)
- Adversarial training leads to mode-collapse (the tendency of adversarial generative models to cover only a subset of modes of a probability distribution, resulting in a failure to produce adequately diverse samples)
- More difficult and slow to train as they do not immediately provide a latent representation of the data
Thus, the former approach can model diverse behaviors without dropping modes but does not learn robust policies, while the latter approach gives robust policies but insufficiently diverse behaviors. Thus, the authors combine the favorable aspects of these two approaches. The base of their model is a new type of variational autoencoder on demonstration trajectories that learns semantic policy embeddings. Leveraging these policy representations, they develop a new version of GAIL that
- is much more robust than the purely-supervised controller, especially with few demonstrations, and
- avoids mode collapse, capturing many diverse behaviors when GAIL on its own does not.
Model
The authors first introduce a variational autoencoder (VAE) for supervised imitation, consisting of a bi-directional LSTM encoder mapping demonstration sequences to embedding vectors, and two decoders. The first decoder is a multi-layer perceptron (MLP) policy mapping a trajectory embedding and the current state to a continuous action vector. The second is a dynamics model mapping the embedding and previous state to the present state while modeling correlations among states with a WaveNet.
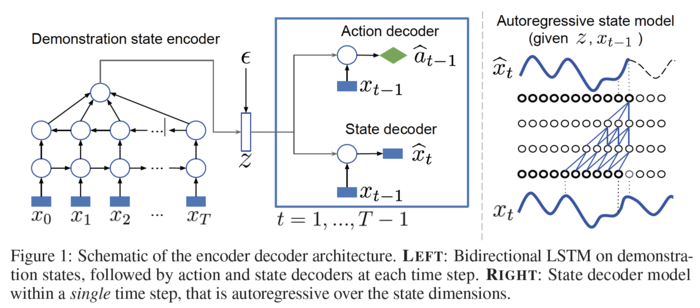
Behavioral cloning with VAE suited for control
In this section, the authors follow a similar approach to Duan et al., but opt for stochastic VAEs as having a distribution [math]\displaystyle{ q_\phi(z|x_{1:T}) }[/math] to better regularize the latent space. In their VAE, an encoder maps a demonstration sequence to an embedding vector [math]\displaystyle{ z }[/math]. Given [math]\displaystyle{ z }[/math], they decode both the state and action trajectories as shown in the figure above. To train the model, the following loss is minimized:
\begin{align} L\left( \alpha, w, \phi; \tau_i \right) = - \pmb{\mathbb{E}}_{q_{\phi}(z|x_{1:T_i}^i)} \left[ \sum_{t=1}^{T_i} log \pi_\alpha \left( a_t^i|x_t^i, z \right) + log p_w \left( x_{t+1}^i|x_t^i, z\right) \right] +D_{KL}\left( q_\phi(z|x_{1:T_i}^i)||p(z) \right) \end{align}
The encoder [math]\displaystyle{ q }[/math] uses a bi-directional LSTM. To produce the final embedding, it calculates the average of all the outputs of the second layer of this LSTM before applying a final linear transformation to generate the mean and standard deviation of a Gaussian. Then, one sample from this Gaussian is taken as the demonstration encoding.
The action decoder is an MLP that maps the concatenation of the state and the embedding of the parameters of a Gaussian policy. The state decoder is similar to a conditional WaveNet model. In particular, it conditions on the embedding [math]\displaystyle{ z }[/math] and previous state [math]\displaystyle{ x_{t-1} }[/math] to generate the vector [math]\displaystyle{ x_t }[/math] autoregressively. That is, the autoregression is over the components of the vector [math]\displaystyle{ x_t }[/math]. Finally, instead of a Softmax, the model uses a mixture of Gaussians as the output of the WaveNet.
Diverse generative adversarial imitiation learning
To enable GAIL to produce diverse solutions, the authors condition the discriminator on the embeddings generated by the VAE encoder and integrate out the GAIL objective with respect to the variational posterior [math]\displaystyle{ q_\phi(z|x_{1:T}) }[/math]. Specifically, the authors train the discriminator by optimizing the following objective:
\begin{align} {max}_{\psi} \pmb{\mathbb{E}}_{\tau_i \sim \pi_E} \left( \pmb{\mathbb{E}}_{q(z|x_{1:T_i}^i)} \left[\frac{1}{T_i} \sum_{t=1}^{T_i} logD_{\psi} \left( x_t^i, a_t^i | z \right) + \pmb{\mathbb{E}}_{\pi_\theta} \left[ log(1 - D_\psi(x, a | z)) \right] \right] \right) \end{align}
The authors condition on unlabeled trajectories, which have been passed through a powerful encoder, and hence this approach is capable of one-shot imitation learning. Moreover, the VAE encoder enables to obtain a continuous latent embedding space where interpolation is possible.
To better motivate the objective, the authors propose on temporarily leaving the context of imitation learning and considering an alternative objective for training GANs
\begin{align} {min}_{G}{max}_{D} V (G, D) = \int_{y} p(y) \int_{z} q(z|y) \left[ log D(y | z) + \int_{\hat{y}} G(\hat{y} | z) log (1 - D(\hat{y} | z)) d\hat{y} \right] dy dz \end{align}
This function is a simplification of the previous objective function. Furthermore, it satisfies the following property.
Lemma 1
Assuming that [math]\displaystyle{ q }[/math] computes the true posterior distribution that is [math]\displaystyle{ q(z|y) = \frac{p(y|z)p(z)}{p(y)} }[/math] then
\begin{align} V (G, D) = \int_{z} p(z) \left[ \int_{y} p(y|z) log D(y|z) dy + \int_{\hat{y}} G(\hat{y} | z) log (1 - D(\hat{y} | z)) d\hat{y} \right] dz \end{align}
If an optimal discriminator is further assumed, the cost optimized by the generator then becomes
\begin{align} C(G) = 2 \int_ p p(z) JSD[p(\cdot|z) || G(\cdot|z)] dz - log4 \end{align}
where [math]\displaystyle{ JSD }[/math] stands for the Jensen-Shannon divergence.
Experiments
The primary focus of the paper's experimental evaluation is to demonstrate that the architecture allows learning of robust controllers capable of producing the full spectrum of demonstration behaviors for a diverse range of challenging control problems. The authors consider three bodies: a 9 DoF robotic arm, a 9 DoF planar walker, and a 62 DoF complex humanoid (56-actuated joint angles, and a freely translating and rotating 3d root joint). While for the reaching task BC is sufficient to obtain a working controller, for the other two problems the full learning procedure is critical.
The authors analyze the resulting embedding spaces and demonstrate that they exhibit a rich and sensible structure that can be exploited for control. Finally, the authors show that the encoder can be used to capture the gist of novel demonstration trajectories which can then be reproduced by the controller.
Robotic arm reaching
In this experiment, the authors demonstrate the effectiveness of their VAE architecture and investigate the nature of the learned embedding space on a reaching task with a simulated Jaco arm.
To obtain demonstrations, the authors trained 60 independent policies to reach to random target locations in the workspace starting from the same initial configuration. 30 trajectories from each of the first 50 policies were generated. These served as training data for the VAE model (1500 training trajectories in total). The remaining 10 policies were used to generate test data.
The reaching task is relatively simple, so with this amount of data the VAE policy is fairly robust. After training, the VAE encodes and reproduces the demonstrations as shown in the figure below.

2D Walker
As a more challenging test compared to the reaching task, the authors consider bipedal locomotion. Here, the authors train 60 neural network policies for a 2d walker to serve as demonstrations. These policies are each trained to move at different speeds both forward and backward depending on a label provided as additional input to the policy. Target speeds for training were chosen from a set of four different speeds (m/s): -1, 0, 1, 3.
The authors trained their model with 20 episodes per policy (1200 demonstration trajectories in total, each with a length of 400 steps or 10s of simulated time). In this experiment a full approach is required: training the VAE with BC alone can imitate some of the trajectories, but it performs poorly in general, presumably because the relatively small training set does not cover the space of trajectories sufficiently densely. On this generated dataset, they also train policies with GAIL using the same architecture and hyper-parameters. Due to the lack of conditioning, GAIL does not reproduce coherently trajectories. Instead, it simply meshes different behaviors together. In addition, the policies trained with GAIL also, exhibit dramatically less diversity; see video.