Robust Imitation of Diverse Behaviors: Difference between revisions
(Added a section on TRPO, the optimization strategy used in policy update.) |
|||
| Line 23: | Line 23: | ||
==Behavioral cloning with VAE suited for control== | ==Behavioral cloning with VAE suited for control== | ||
In this section, the authors follow a similar approach to Duan et al. (2017), but opt for stochastic VAEs as having a distribution <math display="inline">q_\phi(z|x_{1:T})</math> to better regularize the latent space. In their VAE, an encoder maps a demonstration sequence to an embedding vector <math display="inline">z</math>. Given <math display="inline">z</math>, they decode both the state and action trajectories as shown in the figure above. To train the model, the following loss is minimized: | In this section, the authors follow a similar approach to Duan et al. (2017), but opt for stochastic VAEs as having a distribution <math display="inline">q_\phi(z|x_{1:T})</math> to better regularize the latent space. In their VAE, an encoder stochastically maps a demonstration sequence to an embedding vector <math display="inline">z</math>. Given <math display="inline">z</math>, they decode both the state and action trajectories as shown in the figure above. To train the model, the following loss is minimized: | ||
\begin{align} | \begin{align} | ||
L\left( \alpha, w, \phi; \tau_i \right) = - \pmb{\mathbb{E}}_{q_{\phi}(z|x_{1:T_i}^i)} \left[ \sum_{t=1}^{T_i} log \pi_\alpha \left( a_t^i|x_t^i, z \right) + log p_w \left( x_{t+1}^i|x_t^i, z\right) \right] +D_{KL}\left( q_\phi(z|x_{1:T_i}^i)||p(z) \right) | L\left( \alpha, w, \phi; \tau_i \right) = - \pmb{\mathbb{E}}_{q_{\phi}(z|x_{1:T_i}^i)} \left[ \sum_{t=1}^{T_i} log \pi_\alpha \left( a_t^i|x_t^i, z \right) + log p_w \left( x_{t+1}^i|x_t^i, z\right) \right] +D_{KL}\left( q_\phi(z|x_{1:T_i}^i)||p(z) \right) | ||
\end{align} | \end{align} | ||
Where <math> \alpha </math> parameterizes the action decoder, <math> w </math> parameterizes the state decoder, <math> \phi </math> parameterizes the state encoder, and <math> T_i \in \tau_i </math> is the set of demonstration trajectories. | |||
The encoder <math display="inline">q</math> uses a bi-directional LSTM. To produce the final embedding, it calculates the average of all the outputs of the second layer of this LSTM before applying a final linear transformation to | The encoder <math display="inline">q</math> uses a bi-directional LSTM. To produce the final embedding, it calculates the average of all the outputs of the second layer of this LSTM before applying a final linear transformation to | ||
Revision as of 13:07, 21 March 2018
Introduction
One of the longest standing challenges in AI is building versatile embodied agents, both in the form of real robots and animated avatars, capable of a wide and diverse set of behaviors. State-of-the-art robots cannot compete with the effortless variety and adaptive flexibility of motor behaviors produced by toddlers. Towards addressing this challenge, the authors combine several deep generative approaches to imitation learning in a way that accentuates their individual strengths and addresses their limitations. The end product is a robust neural network policy that can imitate a large and diverse set of behaviors using few training demonstrations.
Motivation
Some of the models that have recently shown great promise in imitation learning for motor control are the deep generative models. The authors primarily talk about two approaches viz. supervised approaches that condition on demonstrations and Generative Adversarial Imitation Learning (GAIL) and their limitations and try to combine those two approaches in order to address these limitations. Some of these limitations are as follows:
- Supervised approaches that condition on demonstrations (VAE):
- They require large training datasets in order to work for non-trivial tasks
- They tend to be brittle and fail when the agent diverges too much from the demonstration trajectories (As proof of this brittleness, the authors cite Ross et al. (2010), who provide a theorem showing that the cost incurred by this kind of model when it deviates from a demonstration trajectory with a small probability can be amplified in a manner quadratic in the number of time steps. )
- Generative Adversarial Imitation Learning (GAIL)
- Adversarial training leads to mode-collapse (the tendency of adversarial generative models to cover only a subset of modes of a probability distribution, resulting in a failure to produce adequately diverse samples)
- More difficult and slow to train as they do not immediately provide a latent representation of the data
Thus, the former approach can model diverse behaviors without dropping modes but does not learn robust policies, while the latter approach gives robust policies but insufficiently diverse behaviors. Thus, the authors combine the favorable aspects of these two approaches. The base of their model is a new type of variational autoencoder on demonstration trajectories that learns semantic policy embeddings. Leveraging these policy representations, they develop a new version of GAIL that
- is much more robust than the purely-supervised controller, especially with few demonstrations, and
- avoids mode collapse, capturing many diverse behaviors when GAIL on its own does not.
Model
The authors first introduce a variational autoencoder (VAE) for supervised imitation, consisting of a bi-directional LSTM encoder mapping demonstration sequences to embedding vectors, and two decoders. The first decoder is a multi-layer perceptron (MLP) policy mapping a trajectory embedding and the current state to a continuous action vector. The second is a dynamics model mapping the embedding and previous state to the present state while modeling correlations among states with a WaveNet.
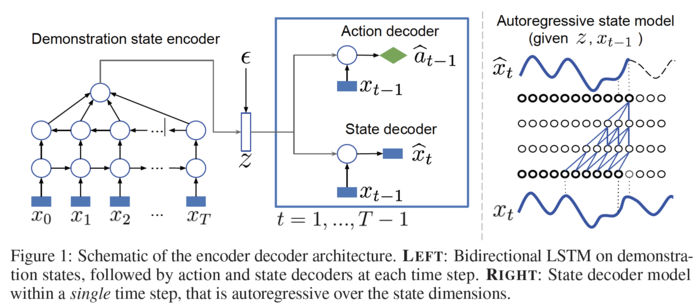
Behavioral cloning with VAE suited for control
In this section, the authors follow a similar approach to Duan et al. (2017), but opt for stochastic VAEs as having a distribution [math]\displaystyle{ q_\phi(z|x_{1:T}) }[/math] to better regularize the latent space. In their VAE, an encoder stochastically maps a demonstration sequence to an embedding vector [math]\displaystyle{ z }[/math]. Given [math]\displaystyle{ z }[/math], they decode both the state and action trajectories as shown in the figure above. To train the model, the following loss is minimized:
\begin{align} L\left( \alpha, w, \phi; \tau_i \right) = - \pmb{\mathbb{E}}_{q_{\phi}(z|x_{1:T_i}^i)} \left[ \sum_{t=1}^{T_i} log \pi_\alpha \left( a_t^i|x_t^i, z \right) + log p_w \left( x_{t+1}^i|x_t^i, z\right) \right] +D_{KL}\left( q_\phi(z|x_{1:T_i}^i)||p(z) \right) \end{align}
Where [math]\displaystyle{ \alpha }[/math] parameterizes the action decoder, [math]\displaystyle{ w }[/math] parameterizes the state decoder, [math]\displaystyle{ \phi }[/math] parameterizes the state encoder, and [math]\displaystyle{ T_i \in \tau_i }[/math] is the set of demonstration trajectories.
The encoder [math]\displaystyle{ q }[/math] uses a bi-directional LSTM. To produce the final embedding, it calculates the average of all the outputs of the second layer of this LSTM before applying a final linear transformation to generate the mean and standard deviation of a Gaussian. Then, one sample from this Gaussian is taken as the demonstration encoding.
The action decoder is an MLP that maps the concatenation of the state and the embedding of the parameters of a Gaussian policy. The state decoder is similar to a conditional WaveNet model. In particular, it conditions on the embedding [math]\displaystyle{ z }[/math] and previous state [math]\displaystyle{ x_{t-1} }[/math] to generate the vector [math]\displaystyle{ x_t }[/math] autoregressively. That is, the autoregression is over the components of the vector [math]\displaystyle{ x_t }[/math]. Finally, instead of a Softmax, the model uses a mixture of Gaussians as the output of the WaveNet.
Diverse generative adversarial imitiation learning
To enable GAIL to produce diverse solutions, the authors condition the discriminator on the embeddings generated by the VAE encoder and integrate out the GAIL objective with respect to the variational posterior [math]\displaystyle{ q_\phi(z|x_{1:T}) }[/math]. Specifically, the authors train the discriminator by optimizing the following objective:
\begin{align} {max}_{\psi} \pmb{\mathbb{E}}_{\tau_i \sim \pi_E} \left( \pmb{\mathbb{E}}_{q(z|x_{1:T_i}^i)} \left[\frac{1}{T_i} \sum_{t=1}^{T_i} logD_{\psi} \left( x_t^i, a_t^i | z \right) + \pmb{\mathbb{E}}_{\pi_\theta} \left[ log(1 - D_\psi(x, a | z)) \right] \right] \right) \end{align}
The authors condition on unlabeled trajectories, which have been passed through a powerful encoder, and hence this approach is capable of one-shot imitation learning. Moreover, the VAE encoder enables to obtain a continuous latent embedding space where interpolation is possible.
To better motivate the objective, the authors propose on temporarily leaving the context of imitation learning and considering an alternative objective for training GANs
\begin{align} {min}_{G}{max}_{D} V (G, D) = \int_{y} p(y) \int_{z} q(z|y) \left[ log D(y | z) + \int_{\hat{y}} G(\hat{y} | z) log (1 - D(\hat{y} | z)) d\hat{y} \right] dy dz \end{align}
This function is a simplification of the previous objective function. Furthermore, it satisfies the following property.
Lemma 1
Assuming that [math]\displaystyle{ q }[/math] computes the true posterior distribution that is [math]\displaystyle{ q(z|y) = \frac{p(y|z)p(z)}{p(y)} }[/math] then
\begin{align} V (G, D) = \int_{z} p(z) \left[ \int_{y} p(y|z) log D(y|z) dy + \int_{\hat{y}} G(\hat{y} | z) log (1 - D(\hat{y} | z)) d\hat{y} \right] dz \end{align}
If an optimal discriminator is further assumed, the cost optimized by the generator then becomes
\begin{align} C(G) = 2 \int_ p p(z) JSD[p(\cdot|z) || G(\cdot|z)] dz - log4 \end{align}
where [math]\displaystyle{ JSD }[/math] stands for the Jensen-Shannon divergence. In the context of the WaveNet described in the earlier section, [math]\displaystyle{ p(x) }[/math] is the distribution of a mixture of Gaussians, and [math]\displaystyle{ p(z) }[/math] is the distribution over the mixture components, so the conditional distribution over the latent [math]\displaystyle{ z }[/math], [math]\displaystyle{ p(x | z) }[/math] is uni-modal, and optimizing the divergence will not lead to mode collapse.
Policy Optimization Strategy: TRPO
In Algorithm 1, it states that TRPO is used for policy parameter updates. TRPO is short for Trust Region Policy Optimization, which an iterative procedure for policy optimization, developed by John Schulman, Sergey Levine, Philip Moritz, Micheal Jordan and Pieter Abbeel. This optimization methods achieves monotonic improve in fields related to robotic motions, such as walking and swimming. For more details on TRPO, please refer to the original paper.
Experiments
The primary focus of the paper's experimental evaluation is to demonstrate that the architecture allows learning of robust controllers capable of producing the full spectrum of demonstration behaviors for a diverse range of challenging control problems. The authors consider three bodies: a 9 DoF robotic arm, a 9 DoF planar walker, and a 62 DoF complex humanoid (56-actuated joint angles, and a freely translating and rotating 3d root joint). While for the reaching task BC is sufficient to obtain a working controller, for the other two problems the full learning procedure is critical.
The authors analyze the resulting embedding spaces and demonstrate that they exhibit a rich and sensible structure that can be exploited for control. Finally, the authors show that the encoder can be used to capture the gist of novel demonstration trajectories which can then be reproduced by the controller.
Robotic arm reaching
In this experiment, the authors demonstrate the effectiveness of their VAE architecture and investigate the nature of the learned embedding space on a reaching task with a simulated Jaco arm.
To obtain demonstrations, the authors trained 60 independent policies to reach to random target locations in the workspace starting from the same initial configuration. 30 trajectories from each of the first 50 policies were generated. These served as training data for the VAE model (1500 training trajectories in total). The remaining 10 policies were used to generate test data.
Here are the trajectories produced by the VAE model.
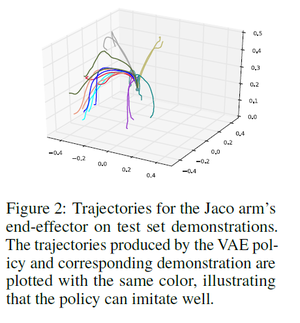
The reaching task is relatively simple, so with this amount of data the VAE policy is fairly robust. After training, the VAE encodes and reproduces the demonstrations as shown in the figure below.

2D Walker
As a more challenging test compared to the reaching task, the authors consider bipedal locomotion. Here, the authors train 60 neural network policies for a 2d walker to serve as demonstrations. These policies are each trained to move at different speeds both forward and backward depending on a label provided as additional input to the policy. Target speeds for training were chosen from a set of four different speeds (m/s): -1, 0, 1, 3.
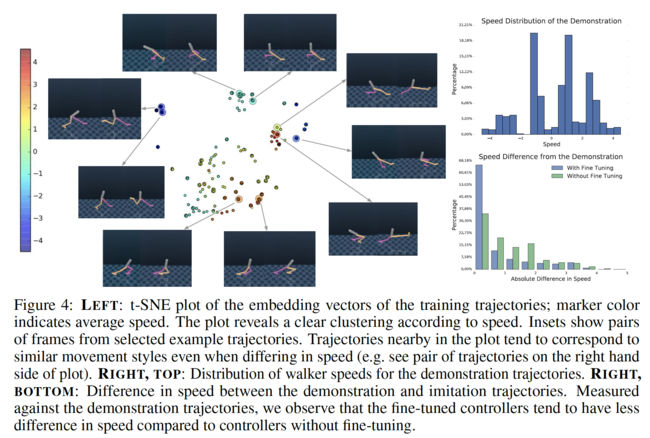
The authors trained their model with 20 episodes per policy (1200 demonstration trajectories in total, each with a length of 400 steps or 10s of simulated time). In this experiment a full approach is required: training the VAE with BC alone can imitate some of the trajectories, but it performs poorly in general, presumably because the relatively small training set does not cover the space of trajectories sufficiently densely. On this generated dataset, they also train policies with GAIL using the same architecture and hyper-parameters. Due to the lack of conditioning, GAIL does not reproduce coherently trajectories. Instead, it simply meshes different behaviors together. In addition, the policies trained with GAIL also, exhibit dramatically less diversity; see video.

Complex humanoid
For this experiment, the authors consider a humanoid body of high dimensionality that poses a hard control problem. They generate training trajectories with the existing controllers, which can produce instances of one of six different movement styles. Examples of such trajectories are shown in Fig. 5.
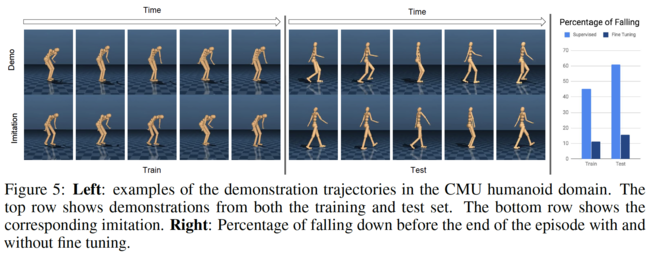
The training set consists of 250 random trajectories from 6 different neural network controllers that were trained to match 6 different movement styles from the CMU motion capture database. Each trajectory is 334 steps or 10s long. The authors use a second set of 5 controllers from which they generate trajectories for evaluation (3 of these policies were trained on the same movement styles as the policies used for generating training data).
Surprisingly, despite the complexity of the body, supervised learning is quite effective at producing sensible controllers: The VAE policy is reasonably good at imitating the demonstration trajectories, although it lacks the robustness to be practically useful. Adversarial training dramatically improves the stability of the controller. The authors analyze the improvement quantitatively by computing the percentage of the humanoid falling down before the end of an episode while imitating either training or test policies. The results are summarized in Figure 5 right. The figure further shows sequences of frames of representative demonstration and associated imitation trajectories. Videos of demonstration and imitation behaviors can be found in the video.

Also, for practical purposes, it is desirable to allow the controller to transition from one behavior to another. The authors test this possibility in an experiment similar to the one for the Jaco arm: They determine the embedding vectors of pairs of demonstration trajectories, start the trajectory by conditioning on the first embedding vector, and then transition from one behavior to the other half-way through the episode by linearly interpolating the embeddings of the two demonstration trajectories over a window of 20 control steps. Although not always successful the learned controller often transitions robustly, despite not having been trained to do so. An example of this can be seen in the gif above. More examples can be seen in this video.
Conclusions
The authors have proposed an approach for imitation learning that combines the favorable properties of techniques for density modeling with latent variables (VAEs) with those of GAIL. The result is a model that from a moderate number of demonstration tragectories, can learn:
- a semantically well structured embedding of behaviors,
- a corresponding multi-task controller that allows to robustly execute diverse behaviors from this embedding space, as well as
- an encoder that can map new trajectories into the embedding space and hence allows for one-shot imitation.
The experimental results demonstrate that this approach can work on a variety of control problems and that it scales even to very challenging ones such as the control of a simulated humanoid with a large number of degrees of freedoms.
Critique
The paper proposes a deep-learning-based approach to imitation learning which is sample-efficient and is able to imitate many diverse behaviors. The architecture can be seen as conditional generative adversarial imitation learning (GAIL). The conditioning vector is an embedding of a demonstrated trajectory, provided by a variational autoencoder. This results in one-shot imitation learning: at test time, a new demonstration can be embedded and provided as a conditioning vector to the imitation policy. The authors evaluate the method on several simulated motor control tasks.
Pros:
- Addresses a challenging problem of learning complex dynamics controllers / control policies
- Well-written introduction / motivation
- The proposed approach is able to learn complex and diverse behaviors and outperforms both the VAE alone (quantitatively) and GAIL alone (qualitatively).
- Appealing qualitative results on the three evaluation problems. Interesting experiments with motion transitioning.
Cons:
- Comparisons to baselines could be more detailed.
- Many key details are omitted (either on purpose, placed in the appendix, or simply absent, like the lack of definitions of terms in the modeling section, details of the planner model, simulation process, or the details of experimental settings)
- Experimental evaluation is largely subjective (videos of robotic arm/biped/3D human motion)
- A discussion of sample efficiency compared to GAIL and VAE would be interesting.
- The presentation is not always clear, in particular, I had a hard time figuring out the notation in Section 3.
- There has been some work on hybrids of VAEs and GANs, which seem worth mentioning when generative models are discussed, like:
- Autoencoding beyond pixels using a learned similarity metric, Larsen et al., ICML 2016
- Generating Images with Perceptual Similarity Metrics based on Deep Networks, Dosovitskiy&Brox. NIPS 2016
These works share the intuition that good coverage of VAEs can be combined with sharp results generated by GANs.
- Some more extensive analysis of the approach would be interesting. How sensitive is it to hyperparameters? How important is it to use VAE, not usual AE or supervised learning? How difficult will it be for others to apply it to new tasks?
References
- Duan, Y., Andrychowicz, M., Stadie, B., Ho, J., Schneider, J., Sutskever, I., Abbeel, P., & Zaremba, W. (2017). One-shot imitation learning. Preprint arXiv:1703.07326.
- Ross, Stéphane, and Drew Bagnell. "Efficient reductions for imitation learning." Proceedings of the thirteenth international conference on artificial intelligence and statistics. 2010.
- Wang, Z., Merel, J. S., Reed, S. E., de Freitas, N., Wayne, G., & Heess, N. (2017). Robust imitation of diverse behaviors. In Advances in Neural Information Processing Systems (pp. 5326-5335).
- https://deepmind.com/blog/producing-flexible-behaviours-simulated-environments/
- https://www.youtube.com/watch?v=NaohsyUxpxw
- https://www.youtube.com/watch?v=VBrIll0B24o