Robot Learning in Homes: Improving Generalization and Reducing Dataset Bias

Introduction

The use of data-driven approaches in robotics has increased in the last decade. Instead of using hand-designed models, these data-driven approaches work on large-scale datasets and learn appropriate policies that map from high-dimensional observations to actions. Since collecting data using an actual robot in real-time is very expensive, most of the data-driven approaches in robotics use simulators in order to collect simulated data. The concern here is whether these approaches have the capability to be robust enough to domain shift and to be used for real-world data. It is an undeniable fact that there is a wide reality gap between simulators and the real world.

This has motivated the robotics community to increase their efforts in collecting real-world physical interaction data for a variety of tasks. This effort has been accelerated by the declining costs of hardware. This approach has been quite successful at tasks such as grasping, pushing, poking and imitation learning. However, the major problem is that the performance of these learning models are not good enough and tend to plateau fast. Furthermore, robotic action data did not lead to similar gains in other areas such as computer vision and natural language processing. As the paper claimed, the solution for all of these obstacles is using “real data”. Current robotic datasets lack diversity of environment. Learning-based approaches need to move out of simulators in the labs and go to real environments such as real homes so that they can learn from real datasets.

Like every other process, the process of collecting real-world data is made difficult by a number of problems. First, there is a need for cheap and compact robots to collect data in homes but current industrial robots (i.e. Sawyer and Baxter) are too expensive. Secondly, cheap robots are not accurate enough to collect reliable data. Also, there is a lack of constant supervision for data collection in homes. Finally, there is also a circular dependency problem in home-robotics: there is a lack of real-world data which are needed to improve current robots, but current robots are not good enough to collect reliable data in homes. These challenges in addition to some other external factors will likely result in noisy data collection. In this paper, a first systematic effort has been presented for collecting a dataset inside homes. In accomplishing this goal, the authors:

1. Build a cheap robot costing less than USD 3K which is appropriate for use in homes

2. Collect training data in 6 different homes and testing data in 3 homes

3. Propose a method for modelling the noise in the labelled data

4. Demonstrate that the diversity in the collected data provides superior performance and requires little-to-no domain adaptation

Overview

This paper emphasizes the importance of diversifying the data for robotic learning in order to have a greater generalization, by focusing on the task of grasping. A diverse dataset also allows for removing biases in the data. By considering these facts, the paper argues that even for simple tasks like grasping, datasets which are collected in labs suffer from strong biases such as simple backgrounds and same environment dynamics. Hence, the learning approaches cannot generalize the models and work well on real datasets.

As a future possibility, there would be a need for having a low-cost robot to collect large-scale data inside a huge number of homes. For this reason, they introduced a customized mobile manipulator. They used a Dobot Magician which is a robotic arm mounted on a Kobuki which is a low-cost mobile robot base equipped with sensors such as bumper contact sensors and wheel encoders. The resulting robot arm has five degrees of freedom (DOF) (x, y, z, roll, pitch). The gripper is a two-fingered electric gripper with a 0.3kg payload. They also add an Intel R200 RGBD camera to their robot which is at a height of 1m above the ground. An Intel Core i5 processor is also used as an onboard laptop to perform all the processing. The whole system can run for 1.5 hours with a single charge.

As there is always a trade-off, when we gain a low-cost robot, we are actually losing accuracy for controlling it. So, the low-cost robot which is built from cheaper components than the expensive setups such as Baxter and Sawyer suffers from higher calibration errors and execution errors. This means that the dataset collected with this approach is diverse and huge but it has noisy labels. To illustrate, consider when the robot wants to grasp at location [math]\displaystyle{ {(x, y)} }[/math]. Since there is a noise in the execution, the robot may perform this action in the location [math]\displaystyle{ {(x + \delta_{x}, y+ \delta_{y})} }[/math] which would assign the success or failure label of this action to a wrong place. Therefore, to solve the problem, they used an approach to learn from noisy data. They modeled noise as a latent variable and used two networks, one for predicting the noise and one for predicting the action to execute.

Learning on low-cost robot data

This paper uses a patch grasping framework in its proposed architecture. Also, as mentioned before, there is a high tendency for noisy labels in the datasets which are collected by inaccurate and cheap robots. The cause of the noise in the labels could be due to the hardware execution error, inaccurate kinematics, camera calibration, proprioception, wear, and tear, etc. Here are more explanations about different parts of the architecture in order to disentangle the noise of the low-cost robot’s actual and commanded executions.

Grasping Formulation

Planar grasping is the object of interest in this architecture. It means that all the objects are grasped at the same height and vertical to the ground (ie: a fixed end-effector pitch). The object is fixed in the z direction and basically perpendicular to the ground. The final goal is to find [math]\displaystyle{ {(x, y, \theta)} }[/math] given an observation [math]\displaystyle{ {I} }[/math] of the object, where [math]\displaystyle{ {x} }[/math] and [math]\displaystyle{ {y} }[/math] are the translational degrees of freedom and [math]\displaystyle{ {\theta} }[/math] is the rotational degrees of freedom (roll of the end-effector). For the purpose of comparison, they used a model which does not predict the [math]\displaystyle{ {(x, y, \theta)} }[/math] directly from the image [math]\displaystyle{ {I} }[/math], but samples several smaller patches [math]\displaystyle{ {I_{P}} }[/math] at different locations [math]\displaystyle{ {(x, y)} }[/math]. Thus, the angle of grasp [math]\displaystyle{ {\theta} }[/math] is predicted from these patches. Also, in order to have multi-modal predictions, discrete steps of the angle [math]\displaystyle{ {\theta} }[/math], [math]\displaystyle{ {\theta_{D}} }[/math] is used.

Hence, each datapoint consists of an image [math]\displaystyle{ {I} }[/math], the executed grasp [math]\displaystyle{ {(x, y, \theta)} }[/math] and the grasp success/failure label g. Then, the image [math]\displaystyle{ {I} }[/math] and the angle [math]\displaystyle{ {\theta} }[/math] are converted to image patch [math]\displaystyle{ {I_{P}} }[/math] and angle [math]\displaystyle{ {\theta_{D}} }[/math]. Then, to minimize the classification error, a binary cross entropy loss is used which minimizes the error between the predicted and ground truth label [math]\displaystyle{ g }[/math]. A convolutional neural network with weight initialization from pre-training on Imagenet is used for this formulation.

(Note: On Cross Entropy:

If we think of a distribution as the tool we use to encode symbols, then entropy measures the number of bits we'll need if we use the correct tool. This is optimal, in that we can't encode the symbols using fewer bits on average. In contrast, cross entropy is the number of bits we'll need if we encode symbols from [math]\displaystyle{ y }[/math] using the wrong tool [math]\displaystyle{ {\hat h} }[/math] . This consists of encoding the [math]\displaystyle{ {i_{th}} }[/math] symbol using [math]\displaystyle{ {\log(\frac{1}{{\hat h_i}})} }[/math] bits instead of [math]\displaystyle{ {\log(\frac{1}{{ h_i}})} }[/math] bits. We of course still take the expected value to the true distribution y , since it's the distribution that truly generates the symbols:

\begin{align} H(y,\hat y) = \sum_i{y_i\log{\frac{1}{\hat y_i}}} \end{align}

Cross entropy is always larger than entropy; encoding symbols according to the wrong distribution [math]\displaystyle{ {\hat y} }[/math] will always make us use more bits. The only exception is the trivial case where y and [math]\displaystyle{ {\hat y} }[/math] are equal, and in this case entropy and cross entropy are equal.)

Modeling noise as latent variable

In order to tackle the problem of inaccurate position control and calibration due to cheap robot, they found a structure in the noise which is dependent on the robot and the design. They modeled this structure of noise as a latent variable and decoupled during training. The approach is shown in figure 2:

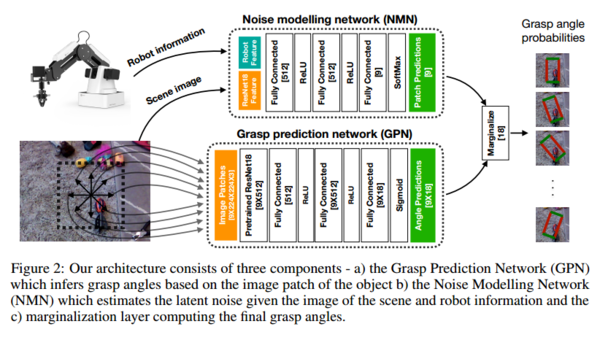
The conventional approach models the grasp success probability for a given image patch at a given angle where the variables of the environment which can introduce noise in the system is generally insignificant, due to the high accuracy of expensive, commercial robots. However, in the low cost setting with multiple robots collecting data in parallel, it becomes an important consideration for learning.

The grasp success probability for image patch [math]\displaystyle{ {I_{P}} }[/math] at angle [math]\displaystyle{ {\theta_{D}} }[/math] is represented as [math]\displaystyle{ {P(g|I_{P},\theta_{D}; \mathcal{R} )} }[/math] where [math]\displaystyle{ \mathcal{R} }[/math] represents environment variables that can add noise to the system.

The conditional probability of grasping at a noisy image patch [math]\displaystyle{ I_P }[/math] for this model is computed by:

\[ { P(g|I_{P},\theta_{D}, \mathcal{R} ) = ∑_{( \widehat{I_P} \in \mathcal{P})} P(g│z=\widehat{I_P},\theta_{D},\mathcal{R}) \cdot P(z=\widehat{I_P} | \theta_{D},I_P,\mathcal{R})} \]

Here, [math]\displaystyle{ {z} }[/math] models the latent variable of the actual patch executed, and [math]\displaystyle{ \widehat{I_P} }[/math] belongs to a set of possible neighboring patches [math]\displaystyle{ \mathcal{P} }[/math].[math]\displaystyle{ P(z=\widehat{I_P}|\theta_D,I_P,\mathcal{R}) }[/math] shows the noise which can be caused by [math]\displaystyle{ \mathcal{R} }[/math] variables and is implemented as the Noise Modelling Network (NMN). [math]\displaystyle{ {P(g│z=\widehat{I_P},\theta_{D}, \mathcal{R} )} }[/math] shows the grasp prediction probability given the true patch and is implemented as the Grasp Prediction Network (GPN). The overall Robust-Grasp model is computed by marginalizing GPN and NMN.

Learning the latent noise model

This section concerns what be the inputs to the NMN network should be and how should the inputs can be trained. The authors assume that [math]\displaystyle{ {z} }[/math] is conditionally independent of the local patch-specific variables [math]\displaystyle{ {(I_{P}, \theta_{D})} }[/math]. To estimate the latent variable [math]\displaystyle{ {z} }[/math] given the global information [math]\displaystyle{ \mathcal{R} }[/math], i.e [math]\displaystyle{ P(z=\widehat{I_P}|\theta_D,I_P,\mathcal{R}) \equiv P(z=\widehat{I_P}|\mathcal{R}) }[/math]. Apart from the patch [math]\displaystyle{ I_{P} }[/math] and grasp information [math]\displaystyle{ (x, y, θ) }[/math], they use information like image of the entire scene, ID of the robot and the location of the raw pixel. They argue that the image of the full scene could contain some essential information about the system such as the relative location of camera to the ground which may change over the lifetime of the robot. The identification number of the robot might give cues about errors specific to a particular hardware. Finally, the raw pixels of execution contain calibration specific information, since calibration error is coupled with pixel location, since least squares fit are used to to compute calibration parameters.

They used direct optimization to learn both NMN and GPN with noisy labels. However, explicit labels are not available to train NMN but the latent variable [math]\displaystyle{ z }[/math] can be estimated using a technique such as Expectation-Maximization. The entire image of the scene and the environment information are the inputs of the NMN, as well as robot ID and raw-pixel grasp location. The output of the NMN is the probability distribution of the actual patches where the grasps are executed. Finally, a binary cross entropy loss is applied to the marginalized output of these two networks and the true grasp label [math]\displaystyle{ g }[/math].

Training details

They implemented their model in PyTorch and fine tuned a pretrained ResNet-18 model. They concatenated 512 dimensional ResNet feature with a 1-hot vector of robot ID and the raw pixel location of the grasp for their NMN. This passes through a series of three fully connected layers and a SoftMax layer to convert the correct patch predictions to a probability distribution. Also, the inputs of the GPN are the original noisy patch plus 8 other equidistant patches from the original one. The angle predictions for all the patches are passed through a sigmoid activation at the end to obtain grasp success probability for a specific patch at a specific angle.

The training of the network takes place in two stages. It starts with training only GPN over 5 epochs of the data. Then, the NMN and the marginalization operator are added to the model. So, they train NMN and GPN simultaneously in an end-to-end fashion for the other 25 epochs.

This two-stage approach is crucial for effective training of their networks, without which NMN trivially selects the same patch irrespective of the input. The optimizer used for training is Adam [16].

Results

In the results part of the paper, they show that collecting dataset in homes is essential for generalizing learning from unseen environments. They also show that modelling the noise in their Low-Cost Arm (LCA) can improve grasping performance.

They collected data about planar grasping. This was done in parallel using multiple robots in 6 different homes, as shown in Figure 3. They used an object detector (tiny-YOLO) as the input data were unstructured due to LCA limited memory and computational capabilities. With an object location detected, object class information was discarded and used only the 2D location for making a sample grasp.The grasp location in 3D was computed using PointCloud data. They scattered different objects in homes within 2m area to prevent collision of the robot with obstacles and let the robot move randomly and grasp objects. Finally, they collected a dataset with 28K grasp results.

To evaluate their approach in a more quantitative way, they used three test settings:

- The first one is a binary classification or held-out data. The test set is collected by performing random grasps on objects. They measure the performance of binary classification by predicting the success or failure of grasping, given a location and the angle. Using binary classification allows for testing a lot of models without running them on real robots. They collected two held-out datasets using LCA in lab and homes and the dataset for Baxter robot.

- The second one is Real Low-Cost Arm (Real-LCA). Here, they evaluate their model by running it in three unseen homes. They put 20 new objects in these three homes in different orientations. Since the objects and the environments are completely new, this tests could measure the generalization of the model.

- The third one is Real Sawyer (Real-Sawyer). They evaluate the performance of their model by running the model on the Sawyer robot which is more accurate than the LCA. They tested their model in the lab environment to show that training models with the datasets collected from homes can improve the performance of models even in lab environments. Since Sawyer , is a more accurate and better calibrated, the Robust-Grasp model was evaluated against the model which doesnot disentangle the noise in the data.

They used baselines for both their data which is collected in homes and their model which is Robust-Grasp. They used two datasets for the baseline. The dataset collected by (Lab-Baxter) and the dataset collected by their LCA in the lab (Lab-LCA). They compared their Robust-Grasp model with the noise independent patch grasping model (Patch-Grasp) [4]. They also compared their data and model with DexNet-3.0 (DexNet) for a strong real-world grasping baseline.

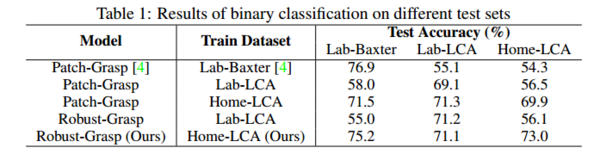
Experiment 1: Performance on held-out data

Table 1 shows that the models trained on lab data cannot generalize to the Home-LCA environment (i.e. they overfit to their respective environments and attain a lower binary classification score). However, the model trained on Home-LCA has a good performance on both lab data and home environment.

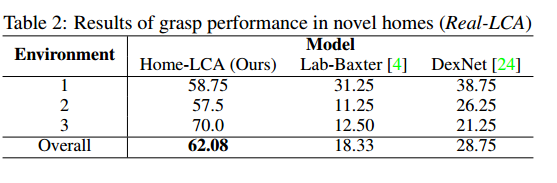
Experiment 2: Performance on Real LCA Robot

In table 2, the performance of the Home-LCA is compared against a pre-trained DexNet and the model trained on the Lab-Baxter. Training on the Home-LCA dataset performs 43.7% better than training on the Lab-Baxter dataset and 33% better than DexNet. The low performance of DexNet can be described by the possible noise in the depth images that are caused by the natural light. DexNet, which requires high-quality depth sensing, cannot perform well in these scenarios. By using cheap commodity RGBD cameras in LCA, the noise in the depth images is not a matter of concern, as the model has no expectation of high-quality sensing.

Performance on Real Sawyer

To compare the performance of the Robust-Grasp model against the Patch-Grasp model without collecting noise-free data, they used Lab-Baxter for benchmarking, which is an accurate and better-calibrated robot. The Sawyer robot is used for testing to ensure that the testing robot is different from both training robots. As shown in Table 3, the Robust-Grasp model trained on Home-LCA outperforms the Patch-Grasp model and achieves 77.5% accuracy which is similar to several recent learning to grasp papers. This accuracy is similar to several recent papers, however, this model was trained and tested in a different environment. The Robust-Grasp model also outperforms the Patch-Grasp by about 4% on binary classification. Furthermore, the visualizations of predicted noise corrections in Figure 4 shows that the corrections depend on both the pixel locations of the noisy grasp and the robot.

Related work

Over the last few years, the interest of scaling up robot learning with large-scale datasets has been increased. Hence, many papers were published in this area. A hand annotated grasping dataset, a self-supervised grasping dataset, and grasping using reinforcement learning are some examples of using large-scale datasets for grasping. The work mentioned above used high-cost hardware and data labeling mechanisms. There were also many papers that worked on other robotic tasks like material recognition, pushing objects and manipulating a rope. However, none of these papers worked on real data in real environments like homes, they all used lab data.

Furthermore, since grasping is one of the basic problems in robotics, there were some efforts to improve grasping. Classical approaches focused on physics-based issues of grasping and required 3D models of the objects. However, recent works focused on data-driven approaches which learn from visual observations to grasp objects. Simulation and real-world robots are both required for large-scale data collection. A versatile grasping model was proposed to achieve a 90% performance for a bin-picking task. The point here is that they usually require high-quality depth as input which seems to be a barrier for practical use of robots in real environments. High-quality depth sensing means a high cost to implement in hardware and thus is a barrier for practical use.

Most labs use industrial robots or standard collaborative hardware for their experiments. Therefore, there is few research that used low-cost robots. One of the examples is learning using a cheap inaccurate robot for stack multiple blocks. Although mobile robots like iRobot’s Roomba have been in the home consumer electronics market for a decade, it is not clear whether learning approaches are used in it alongside mapping and planning.

Learning from noisy inputs is another challenge specifically in computer vision. A controversial question which is often raised in this area is whether learning from noise can improve the performance. Some works show it could have bad effects on the performance; however, some other works find it valuable when the noise is independent or statistically dependent on the environment. In this paper, they used a model that can exploit the noise and learn a better grasping model.

Conclusion

All in all, the paper presents an approach for collecting large-scale robot data in real home environments. They implemented their approach by using a mobile manipulator which is a lot cheaper than the existing industrial robots and costs under 3K USD. They collected a dataset of 28K grasps in six different homes. In order to solve the problem of noisy labels which were caused by their inaccurate robots, they presented a framework to factor out the noise in the data. They tested their model by physically grasping 20 new objects in three new homes and in the lab. The model trained with home dataset showed 43.7% improvement over the models trained with lab data. Their framework performed 33% better than a baseline DexNet model, which struggled with the typically poor depth sensing in common household environments with a lot of natural light. Their results also showed that their model can improve the grasping performance even in lab environments. They also demonstrated that their architecture for modeling the noise improved the performance by about 10%.

Critiques

This paper does not contain a significant algorithmic contribution. They are just combining a large number of data engineering techniques for the robot learning problem. The authors claim that they have obtained 43.7% more accuracy than baseline models, but it does not seem to be a fair comparison as the data collection happened in simulated settings in the lab for other methods, whereas the authors use the home dataset. The authors must have also discussed safety issues when training robots in real environments as against simulated environments like labs. The authors are encouraging other researchers to look outside the labs, but are not discussing the critical safety issues in this approach.

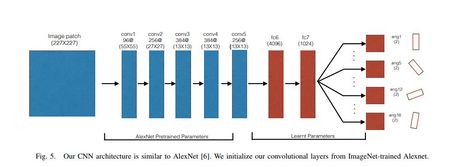
Another strange finding is that the paper mentions that they "follow a model architecture similar to [Pinto and Gupta [4]]," however, the proposed model is, in fact, a fine-tuned resnet-18 architecture. Pinto and Gupta, implement a version similar to AlexNet as shown below in Figure 5.

Figure 5: AlexNet architecture implemented in Pinto and Gupta [4].

The paper argues that the dataset collected by the LCA is noisy, since the robot is cheap and inaccurate. It further asserts that in order to handle the noise in the dataset, they can model the noise as a latent variable and their model can improve the performance of grasping. Although learning from noisy data and achieving a good performance is valuable, it is better that they test their noise modeling network for other robots as well. Since their noise modelling network takes robot information as an input, it would be a good idea to generalize it by testing it using different inaccurate robots to ensure that it would perform well.

They did not mention other aspects of their comparison, for example they could mention their training time compared to other models or the size of other datasets.

References

1. Josh Tobin, Rachel Fong, Alex Ray, Jonas Schneider, Wojciech Zaremba, and Pieter Abbeel. "Domain randomization for transferring deep neural networks from simulation to the real world." 2017. URL https://arxiv.org/abs/1703.06907.
2. Xue Bin Peng, Marcin Andrychowicz, Wojciech Zaremba, and Pieter Abbeel. "Sim-to-real transfer of robotic control with dynamics randomization." arXiv preprint arXiv:1710.06537,2017.
3. Lerrel Pinto, Marcin Andrychowicz, Peter Welinder, Wojciech Zaremba, and Pieter Abbeel. "Asymmetric actor-critic for image-based robot learning." Robotics Science and Systems, 2018.
4. Lerrel Pinto and Abhinav Gupta. "Supersizing self-supervision: Learning to grasp from 50k tries and 700 robot hours." CoRR, abs/1509.06825, 2015. URL http://arxiv.org/abs/1509. 06825.
5. Adithyavairavan Murali, Lerrel Pinto, Dhiraj Gandhi, and Abhinav Gupta. "CASSL: Curriculum accelerated self-supervised learning." International Conference on Robotics and Automation, 2018.
6. Sergey Levine, Chelsea Finn, Trevor Darrell, and Pieter Abbeel. "End-to-end training of deep visuomotor policies." The Journal of Machine Learning Research, 17(1):1334–1373, 2016.
7. Sergey Levine, Peter Pastor, Alex Krizhevsky, and Deirdre Quillen. "Learning hand-eye coordination for robotic grasping with deep learning and large-scale data collection." CoRR, abs/1603.02199, 2016. URL http://arxiv.org/abs/1603.02199.
8. Pulkit Agarwal, Ashwin Nair, Pieter Abbeel, Jitendra Malik, and Sergey Levine. "Learning to poke by poking: Experiential learning of intuitive physics." 2016. URL http://arxiv.org/ abs/1606.07419
9. Chelsea Finn, Ian Goodfellow, and Sergey Levine. "Unsupervised learning for physical interaction through video prediction." In Advances in neural information processing systems, 2016.
10. Ashvin Nair, Dian Chen, Pulkit Agrawal, Phillip Isola, Pieter Abbeel, Jitendra Malik, and Sergey Levine. "Combining self-supervised learning and imitation for vision-based rope manipulation." International Conference on Robotics and Automation, 2017.
11. Chen Sun, Abhinav Shrivastava, Saurabh Singh, and Abhinav Gupta. "Revisiting unreasonable effectiveness of data in deep learning era." ICCV, 2017.
12. Marc Peter Deisenroth, Carl Edward Rasmussen, and Dieter Fox. Learning to control a low-cost manipulator using data-efficient reinforcement learning. RSS, 2011.
13. David F Nettleton, Albert Orriols-Puig, and Albert Fornells. A study of the effect of different types of noise on the precision of supervised learning techniques. Artificial intelligence review, 33(4):275–306, 2010.
14. Benoît Frénay and Michel Verleysen. Classification in the presence of label noise: a survey. IEEE transactions on neural networks and learning systems, 25(5):845–869, 2014.
15. Tong Xiao, Tian Xia, Yi Yang, Chang Huang, and Xiaogang Wang. Learning from massive noisy labeled data for image classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 2691–2699, 2015.
16. Diederik P Kingma and Jimmy Ba. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980, 2014.