Research on Multiple Classification Based on Improved SVM Algorithm for Balanced Binary Decision Tree
Presented By
Aavinash Syamala, Dilmeet Malhi, Sohan Islam, Vansh Joshi
Introduction
According to the Support Vector Machine, if we have a set of m samples: S = {(x1,y1), (x2,y2), …, (xm,ym)}, where xi 𝜖 Rn for all i and yi 𝜖 {-1,1}, and hyperplane wx + b = 0 separate the set exactly with the distance from the hyperplane to the nearest sample is maximum, then this hyperplane will be called an optimal hyperplane. This is also known as the maximum margin hyperplane.
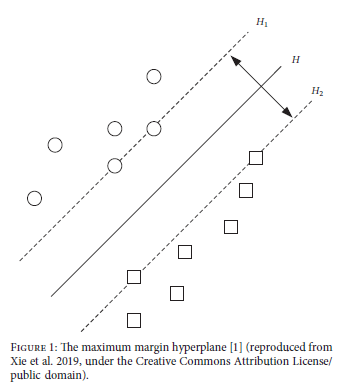
The SVM is much stronger than many other classification methods as we are able to classify in the higher dimensions with the use of Kernel methods. In the kernel methods, we map the sample from the original space to a higher dimension and then we construct a hyperplane that separates the samples in higher-dimensional space.
Using the kernel method leads us to a minimization problem for :
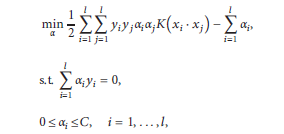
And finally, our final decision function is:
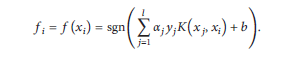
Previous Work
Currently, there are two main multi-classification methods for SVM including the direct method and the indirect method. The solution process of the objective function for the direct method is difficult, especially in the case of a large number of samples, which will greatly increase the difficulty of calculation and solution and increase the training time which results in bad classification accuracy. For this reason, Indirect methods are preferred in practice.
There are many indirect classification methods based on SVM: one-versus-one method, one-versus-all method directed acyclic graph method, error-correcting output codes method, binary decision tree method, and hierarchical multiclass SVM algorithm. The principle of the SVM multiclass classification method based on Decision Tree (DT) is to construct a decision tree recursively so that each layer can separate one or more classes from the rest of the classes. The “error accumulation” phenomenon during the construction process is the error occurring at a certain node will spread to the next layer of nodes, making the classification error of the next level further expand. Therefore, the higher the node where the error occurs the larger the scope of the error’s influence.
The key to reducing the error accumulation is separating the easily distinguishable classes first and reducing the error rate of the upper nodes as much as possible. The binary tree classification algorithm based on SVM uses the minimum distance method as the between-classes separability measure. The separation measure is defined in [1] as “the distance between the centre of two types of samples and the ratio of the variance sum of the two types of samples themselves. However this measure does not take “between classes variance” into consideration which could have a profound impact on the result.
The Design of IBDT-SVM Algorithm
The algorithm divides the samples with the greatest difference step by step according to the new between-classes separability measure to train the classifier and then classifies the rest of the classes according to the class-grouping-by-majority principle to form the new training samples and trains the classifier again. This is how we come up with the IBDT-SVM algorithm.
1. The Improved Between-Classes Separability Measure
To solve the existing problems in the traditional between-classes separability measure inspired by three decision making of clustering, this paper proposes between-classes separability about q neighbours, and the new between-class separability measure considers the following three factors importantly:
(1) The Between-Classes Variance: Considering one sample’s q neighbours in the other neighbour class, its value indicates the degree of separation of one class object from another class.
(2) Class Variance: It reflects the compactness of distribution of samples of the class itself and is inversely proportional to the between-classes separability measure; that is, the smaller the value, the greater the separation of the class from other classes.
(3) Between-Class Distance: It is the distance between two class centres and is proportional to the between-classes separability measure; the greater the values is, the greater the separability of the two classes of samples is.
2. Class Grouping Algorithm Based on the Principle of Class-Grouping by Majority
The IBDT-SVM multiclassification algorithm proposed in this paper improves the between classes separability measure on the basis of considering the between-classes distance, class variance, and between-classes variance. According to the improved between-classes separability measure, the two classes with the highest separability measure are first found and the classification model is trained. Then, it uses the class-grouping-by majority principle to group the other classes into these two groups and use them as the training samples to retrain the classifier. This algorithm loops on each decision surface until each output is a leaf node, that is, a single sample point. This method can ensure that all classes can be separated as far as possible at each classification node and the classification of the rest classes as reasonable as possible. For the data with uneven or sparse distribution, the error caused by the classification method of the minimum distance between class centres can be avoided.
3. The IBDT Algorithm
The algorithm is as follows:
Assume that there are M classes of input data, and class i contains ni samples, then n1+n2+…+ ni = n. The IBDT process is:
Step 1. Set initial q value and calculate the separability measure values of every two classes of samples in M class which is calculated according to the value of separation.
Step 2. Set two maximum between-classes separability measures and let them be class max1 and class max2
Step 3. The classifier is trained by using class max 1 and class max 2 as the training samples which is denoted as the old classifier.
Step 4. According to the principle of the class-grouping-by-majority, which is mentioned above, the remaining class samples are classified into class max 1 and class max 2 and form two major classes {max1, Mi1, Mi2, Mi3, . . . . ., Mij} and {max2, Mij+1, Mij+2, Mij+3, . . . ., MiM-2} and then they are marked as positive samples and negative samples, training the SVM classifier to form the classifier, denoted as our new-classifier.
Step 5. Repeat the process until each sample is labelled as a single category.
The Numerical Experiments and Results
Five multiclass datasets are chosen for 10-fold cross-validation to calculate the classification accuracy for each model. The models include OVO, OVA, BDT-SVM, VBDT-SVM algorithm, and the newly proposed IBDT-SVM algorithm. The datasets chosen have different sample sizes, categories and attributes to see how well the models perform on a wider range of data with different statistical properties. It is to be noted that the OVO algorithm performs considerably well for most datasets except for Breast Tissue where the lack of data could have affected predictions, whereas IBDT-SVM performs comparatively well for all datasets irrespective of different properties as shown in table 2 below. This implies that overall, the IBDT-SVM algorithm has greater stability and improved classification predictions in comparison with the other models. The numerical results can be summarized as shown in table 8 below where the average classification accuracy of all 10 experiments is calculated for each dataset.


Conclusion
In this paper, the authors provide an improvement to the original BDT-SVM method in which originally we consider the distance between the classes. However, the authors suggest using the class variance and the variance between classes. They suggest using the two classes with the maximum difference in order to train the old classifier.
The number of classifiers needed to be constructed is less hence, it makes the algorithm easy and moreover the results also provide evidence on the improvement of classification accuracy as compared to the binary tree classification algorithm.
The authors also discuss the future considerations to further improve the SVM algorithms such as constructing the decision tree based on SVM using the distance between each centre and the root node.
References
[1] S. Y. Xia, H. Pan, and L. Z. Jin, “Multi-class SVM method based on a non-balanced binary tree,” Computer Engineering and Applications, vol. 45, no. 17, pp. 167–169, 2009.
H. Yu and C. K. Mao, “Automatic three-way decision clustering algorithm based on k means,” Computer Applications, vol. 36, no. 8, pp. 2061–2065, 2016.
P. Kantavat, B. Kijsirikul, P. Songsiri, K.-I. Fukui, and M. Numao, “Efficient decision trees for multi-class support vector machines using entropy and generalization error estimation,” International Journal of Applied Mathematics and Computer Science, vol. 28, no. 4, pp. 705–717, 2018.