Reinforcement Learning of Theorem Proving: Difference between revisions
No edit summary |
No edit summary |
||
| Line 28: | Line 28: | ||
In formal terms, the rules of connection calculi is shown in Figure 2, and the formal tableaux for the example sentence is shown in Figure 3. Each leaf is denoted as <math display="inline">subgoal, M, path</math> where <math display="inline">subgoal</math> is a list of literals that we need to find connection later, <math display="inline">M</math> stands for the matrix, and <math display="inline">path</math> stands for the path leading to this leaf. | In formal terms, the rules of connection calculi is shown in Figure 2, and the formal tableaux for the example sentence is shown in Figure 3. Each leaf is denoted as <math display="inline">subgoal, M, path</math> where <math display="inline">subgoal</math> is a list of literals that we need to find connection later, <math display="inline">M</math> stands for the matrix, and <math display="inline">path</math> stands for the path leading to this leaf. | ||
[[file:formal_calculi.png|thumb|center|Figure 2. Formal connection calculi. Adapted from [2]]] | [[file:formal_calculi.png|thumb|center|Figure 2. Formal connection calculi. Adapted from [2].]] | ||
[[file:formal_tableaux.png|thumb|center|Figure 3. Formal tableaux constructed from the example sentence. Adapted from [2]]] | [[file:formal_tableaux.png|thumb|center|Figure 3. Formal tableaux constructed from the example sentence. Adapted from [2].]] | ||
To sum up, the base prover follows a very simple algorithm. given a matrix, a non-negated clause is chosen as the first subgoal. The function ''prove(subgoal, M, path)'' is stated as follows: | To sum up, the base prover follows a very simple algorithm. given a matrix, a non-negated clause is chosen as the first subgoal. The function ''prove(subgoal, M, path)'' is stated as follows: | ||
| Line 49: | Line 49: | ||
[[file:pathological.png|frameless|center]] | [[file:pathological.png|frameless|center]] | ||
However, if we choose <math display="inline">\neg P(x) \lor P(s(x))</math> to do extension, the algorithm will generate an infinite branch <math display="inline">P(0), P(s(0)), P(s(s(0))) ...</math> | However, if we choose <math display="inline">\neg P(x) \lor P(s(x))</math> to do extension, the algorithm will generate an infinite branch <math display="inline">P(0), P(s(0)), P(s(s(0))) ...</math>. It is the task of reinforcement learning to guide the prover in such scenarios towards a successful proof. | ||
In addition, the provability of first order sentences is generally undecidable (this result is named the Church-Turing Thesis), providing us with some insights about the difficulty of automated theorem proving. | |||
== Mizar Math Library == | |||
Mizar Math Library (MML) is a library of mathematical theories. The axioms behind the library is the Tarski-Grothendieck set theory, written in first-order logic. The library contains 57,000+ theorems and their proofs, along with many other lemmas, as well as unproven conjectures. Figure 4 shows a Mizar article of the theorem "If <math display="inline"> p </math> is prime, then <math display="inline"> \sqrt p </math> is irrational." | |||
[[file:mizar_article.png|thumb|center|Figure 3. An article from MML. Adapted from [6].]] | |||
The training and testing data for this paper is a subset of MML, the Mizar 40, which is 32,524 theorems proved by automated theorem provers. Below is an example from the Mizar 40 library, it states that with ''d3_xboole_0'' and ''t3_xboole_0'' as premises, we can prove ''t5_xboole_0''. | |||
[[file:mizar40_0.png|frameless|center]] | |||
[[file:mizar40_1.png|frameless|center]] | |||
[[file:mizar40_2.png|frameless|center]] | |||
[[file:mizar40_3.png|frameless|center]] | |||
== References == | == References == | ||
| Line 61: | Line 75: | ||
[5] A. Alemi, et al. DeepMath-Deep Sequence Models for Premise Selection. NIPS 2016. | [5] A. Alemi, et al. DeepMath-Deep Sequence Models for Premise Selection. NIPS 2016. | ||
[6] Mizar Math Library. http://mizar.org/library/ | |||
Revision as of 21:51, 13 November 2018
Introduction
Automated reasoning over mathematical proof was a major motivation for the development of computer science. Automated theorem provers (ATP) can in principle be used to attack any formally stated mathematical problem, and is a research area that has been studied since the early 20th century. [1] As of today, state-of-art ATP systems rely on fast implementation of complete proof calculi. such as resolution and tableau. However, they are still far weaker than trained mathematicians. Within current ATP systems, many heuristics are essential for their performance. As a result, in recent years machine learning has been used to replace such heuristics and improve the performance of ATPs.
In this paper the authors implemented a reinforcement learning based ATP, rlCoP. The proposed ATP reasons within first-order logic. The underlying proof calculi is the connection calculi [2], and the reinforcement learning method is Monte Carlo tree search along with policy and value learning. It was shown that reinforcement learning results in a 42.1% performance increase compared to the base prover (without learning).
Related Work
C. Kalizyk and J. Urban proposed a supervised learning based ATP, FEMaLeCoP, whose underlying proof calculi is the same as this paper in 2015. [3] In their algorithm learns from existing proofs to choose the next tableau extension step. Similarly, S. Loos, et al. developed an supervised learning ATP system in 2017 [4], with superposition as their proof calculi. However they chose deep neural network (CNNs and RNNs) as feature extractor.
On a different note, A. Alemi, et al. proposed a deep sequence model for premise selection in 2016 [5], and they claim to be the first team to involve deep neural networks in ATPs. Although premise selection is not directly linked to automated reasoning, it is still an important component in ATPs, and their paper provides some insights about how to process datasets of formally stated mathematical problems.
First Order Logic and Connection Calculi
Here we assume basic first-order logic and theorem proving terminology, and we will offer a brief introduction of the base prover and connection calculi. For example, let us try to prove the following first-order sentence.
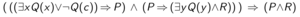
This sentence can be transformed into a formula in Skolemized DNF form, which is referred to as the "matrix".
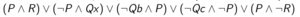
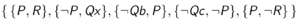
The original first-order sentence is valid if and only if the Skolemized DNF formula is a tautology. The connection calculi attempts to show that the Skolemized DNF formula is a tautology by constructing a tableaux. You will start at the special node, root, which is an open leaf. At each step, you select a clause (for example, clause [math]\displaystyle{ P \wedge R }[/math] is selected in the first step), and add the literals as children for an existing open leaf. For every open leaf, examine the path from root to this leaf. If two literals on this path are unifiable (for example, [math]\displaystyle{ Qx' }[/math] is unifiable with [math]\displaystyle{ \neg Qc }[/math]), this leaf is then closed. In standard terminology it states that a connection is found on this branch.
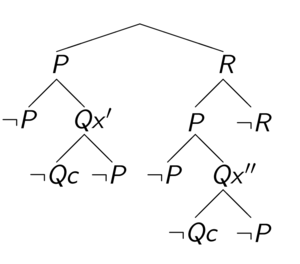
Our goal is to close every leaf, i.e. on every branch, there exists a connection. If such state is reached, we have showed that the Skolemized DNF formula is a tautology, thus proving the original first-order sentence. As we can see from the constructed tableaux, the example sentence is indeed valid.
In formal terms, the rules of connection calculi is shown in Figure 2, and the formal tableaux for the example sentence is shown in Figure 3. Each leaf is denoted as [math]\displaystyle{ subgoal, M, path }[/math] where [math]\displaystyle{ subgoal }[/math] is a list of literals that we need to find connection later, [math]\displaystyle{ M }[/math] stands for the matrix, and [math]\displaystyle{ path }[/math] stands for the path leading to this leaf.


To sum up, the base prover follows a very simple algorithm. given a matrix, a non-negated clause is chosen as the first subgoal. The function prove(subgoal, M, path) is stated as follows:
- If subgoal is empty
- return TRUE
- If reduction is possible
- Perform reduction, generating new_subgoal, new_path
- return prove(new_subgoal, M, new_path)
- For all clauses in M
- If a clause can do extension with subgoal
- Perform extension, generating new_subgoal1, new_path, new_subgoal2
- return prove(new_subgoal1, M, new_path) and prove(new_subgoal2, M, path)
- return FALSE
It is important to note that the base prover implemented in this paper is incomplete. For example, here is a pathological example. Suppose the following matrix (which is trivially a tautology) is feed into the base prover. Let clause [math]\displaystyle{ P(0) }[/math] be the first subgoal. Clearly choosing [math]\displaystyle{ \neg P(0) }[/math] to extend will complete the proof.
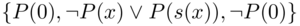
However, if we choose [math]\displaystyle{ \neg P(x) \lor P(s(x)) }[/math] to do extension, the algorithm will generate an infinite branch [math]\displaystyle{ P(0), P(s(0)), P(s(s(0))) ... }[/math]. It is the task of reinforcement learning to guide the prover in such scenarios towards a successful proof.
In addition, the provability of first order sentences is generally undecidable (this result is named the Church-Turing Thesis), providing us with some insights about the difficulty of automated theorem proving.
Mizar Math Library
Mizar Math Library (MML) is a library of mathematical theories. The axioms behind the library is the Tarski-Grothendieck set theory, written in first-order logic. The library contains 57,000+ theorems and their proofs, along with many other lemmas, as well as unproven conjectures. Figure 4 shows a Mizar article of the theorem "If [math]\displaystyle{ p }[/math] is prime, then [math]\displaystyle{ \sqrt p }[/math] is irrational."

The training and testing data for this paper is a subset of MML, the Mizar 40, which is 32,524 theorems proved by automated theorem provers. Below is an example from the Mizar 40 library, it states that with d3_xboole_0 and t3_xboole_0 as premises, we can prove t5_xboole_0.

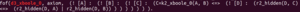


References
[1] C. Kaliszyk, et al. Reinforcement Learning of Theorem Proving. NIPS 2018.
[2] J. Otten and W. Bibel. leanCoP: Lean Connection-Based Theorem Proving. Journal of Symbolic Computation, vol. 36, pp. 139-161, 2003.
[3] C. Kaliszyk and J. Urban. FEMaLeCoP: Fairly Efficient Machine Learning Connection Prover. Lecture Notes in Computer Science. vol. 9450. pp. 88-96, 2015.
[4] S. Loos, et al. Deep Network Guided Proof Search. LPAR-21, 2017.
[5] A. Alemi, et al. DeepMath-Deep Sequence Models for Premise Selection. NIPS 2016.
[6] Mizar Math Library. http://mizar.org/library/