regression on Manifold using Kernel Dimension Reduction
An Algorithm for finding a new linear map for dimension reduction.
Introduction
This paper <ref>[1] Jen Nilsson, Fei Sha, Michael I. Jordan, Regression on Manifold using Kernel Dimension Reduction, 2007</ref> introduces a new algorithm for discovering a manifold that best preserves the information relevant to a non-linear regression. The approach introduced by the authors involves combining the machinery of Kernel Dimension Reduction (KDR) with Laplacian Eigenmaps by optimizing the cross-covariance operators in kernel feature space.
Two main challenges that we usually come across in supervised learning are making a choice of manifold to represent the covariance vector and to choose a function to represent the boundary for classification (i.e. regression surface). As a result of these two complexities, most of the research in supervised learning has been focused on learning linear manifolds. The authors introduce a new algorithm that makes use of methodologies developed in Sufficient Dimension Reduction (SDR) and Kernel Dimension Reduction (KDR). The algorithm is called Manifold Kernel Dimension Reduction (mKDR).
Sufficient Dimension Reduction
The purpose of Sufficient Dimension Reduction (SDR) is to find a linear subspace S such that the response vector Y is conditionally independent of the covariate vector X. More specifically, let [math]\displaystyle{ \,(X,B_X) }[/math] and [math]\displaystyle{ \,(Y,B_Y) }[/math] be measurable spaces of covariates X and response variable Y. S is a subspace if and only if it includes every linear combinations of its elements [2]. If S is a linear subspace of X, it can be imagined as [math]\displaystyle{ \,\{Bv | v \in R^d \} }[/math] where [math]\displaystyle{ \,B \in R^{n \times d} }[/math] and [math]\displaystyle{ \,d \leq n }[/math] are the dimensions of S and X respectively. SDR aims to find a linear subspace [math]\displaystyle{ \,S \subset X }[/math] such that [math]\displaystyle{ \,S }[/math] contains as much predictive information about the response [math]\displaystyle{ \,Y }[/math] as the original covariate space. As seen before in (Fukumizu, K., Bach, F. R., & Jordan, M. I. (2004))<ref>Fukumizu, K., Bach, F. R., & Jordan, M. I. (2004):Kernel Dimensionality Reduction for Supervised Learning</ref> this can be written more formally as a conditional independence assertion.
[math]\displaystyle{ \,Y \perp B^T X | B^T X }[/math] [math]\displaystyle{ \, \Longleftrightarrow Y \perp (X - B^T X) | B^T X }[/math].
The above statement says that [math]\displaystyle{ \,S \subset X }[/math] such that the conditional probability density function [math]\displaystyle{ \,p_{Y|X}(y|x)\, }[/math] is preserved in the sense that [math]\displaystyle{ \,p_{Y|X}(y|x) = p_{Y|B^T X}(y|b^T x)\, }[/math] for all [math]\displaystyle{ \,x \in X \, }[/math] and [math]\displaystyle{ \,y \in Y \, }[/math], where [math]\displaystyle{ \,B^T X\, }[/math] is the orthogonal projection of [math]\displaystyle{ \,X\, }[/math] onto [math]\displaystyle{ \,S\, }[/math]. The subspace [math]\displaystyle{ \,S\, }[/math] is referred to as a dimension reduction subspace. Note that [math]\displaystyle{ \,S\, }[/math] is not unique.
We can define a minimal subspace as the intersection of all dimension reduction subspaces [math]\displaystyle{ \,\,S }[/math]. However, a minimal subspaces will not necessarily satisfy the conditional independence assertion specified above. But when it does, it is referred to as the central subspace.
This is one of the primary goals of the method i.e. to find a central subspace. Several approaches have been introduced in the past, mostly based on inverse regression (Li, 1991)<ref>Sliced inverse regression for dimension reduction. Journal of the American Statistical Association, 86, 316–327</ref> (Li, 1992)<ref>On principal Hessian directions for data visualization and dimension reduction: Another application of Stein’s lemma. Journal of the American Statistical Association, 86, 316–342.</ref>. The main intuition behind this approach is to find [math]\displaystyle{ \,\mathbb{E[} X|Y \mathbb{]} }[/math] becuase if the the forward regression model [math]\displaystyle{ \,\,P(X|Y) }[/math] is concenterated in a subspace of [math]\displaystyle{ \,\,X }[/math], then [math]\displaystyle{ \,\mathbb{E[} X|Y \mathbb{]} }[/math] should also lie in [math]\displaystyle{ \,\,X }[/math] (See Li. 1991 for more details). Unfortunately, such an approach proposes a difficulty of making strong assumptions on the distribution of X (e.g. the distribution should be elliptical) and the methods of inverse regression fail if such assumptions are not satisfied. In order to overcome this problem, the authors turn to the description of KDR, i.e. an approach to SDR which does not make such strong assumptions.
Kernel Dimension Reduction
The framework for Kernel Dimension Reduction was primarily described by Kenji Fukumizu <ref>Fukumizu, K., Bach, F. R., & Jordan, M. I. (2004). Dimensionality reduction for supervised learning with reproducing kernel Hilbert spaces. Journal of Machine Learning Research, 5, 73–99.</ref>. The key idea behind KDR is to map random variables X and Y to Reproducing Kernel Hilbert Spaces (RHKS). Before going ahead, we make some preliminary definitions.
- [math]\displaystyle{ \,\mathbb{D} }[/math]:- Reproducing Kernel Hilbert Space
A Hilbert space is a (possibly infinite dimension) inner product space that is a complete metric space. Elements of a Hilbert space may be functions. A reproducing kernel Hilbert space is a Hilbert space of functions on some set [math]\displaystyle{ \,T }[/math] such that there exists a function [math]\displaystyle{ \,K }[/math] (known as the reproducing kernel) on [math]\displaystyle{ \,T \times T }[/math], where for any [math]\displaystyle{ \,t \in T }[/math], [math]\displaystyle{ \,K( \cdot , t ) }[/math] is in the RKHS.
- [math]\displaystyle{ \,\mathbb{D} }[/math]:- Cross-Covariance Operators
Let [math]\displaystyle{ \,({ H}_1, k_1) }[/math] and [math]\displaystyle{ \,({H}_2, k_2) }[/math] be RKHS over [math]\displaystyle{ \,(\Omega_1, { B}_1) }[/math] and [math]\displaystyle{ \,(\Omega_2, {B}_2) }[/math], respectively, with [math]\displaystyle{ \,k_1 }[/math] and [math]\displaystyle{ \,k_2 }[/math] measurable. For a random vector [math]\displaystyle{ \,(X, Y) }[/math] on [math]\displaystyle{ \,\Omega_1 \times \Omega_2 }[/math]. Using the Reisz representation theorem, one may show that there exists a unique operator [math]\displaystyle{ \,\Sigma_{YX} }[/math] from [math]\displaystyle{ \,H_1 }[/math] to [math]\displaystyle{ \,H_2 }[/math] such that
[math]\displaystyle{ \,\lt g, \Sigma_{YX} f\gt _{H_2} = \mathbb{E}_{XY} [f(X)g(Y)] - \mathbb{E}[f(X)]\mathbb{E}[g(Y)] }[/math]
holds for all [math]\displaystyle{ \,f \in H_1 }[/math] and [math]\displaystyle{ \,g \in H_2 }[/math], which is called the cross-covariance operator.
- [math]\displaystyle{ \,\mathbb{D} }[/math]:- Condtional Covariance Operators
Let [math]\displaystyle{ \,(H_1, k_1) }[/math] and [math]\displaystyle{ \,(H_2, k_2) }[/math] be RKHS on [math]\displaystyle{ \,\Omega_1 \times \Omega_2 }[/math], and let [math]\displaystyle{ \,(X,Y) }[/math] be a random vector on measurable space [math]\displaystyle{ \,\Omega_1 \times \Omega_2 }[/math]. The conditional cross-covariance operator of [math]\displaystyle{ \,(Y,Y) }[/math] given [math]\displaystyle{ \,X }[/math] is defined by
[math]\displaystyle{ \,\Sigma_{YY|x}: = \Sigma_{YY} - \Sigma_{YX}\Sigma_{XX}^{-1}\Sigma_{XY} }[/math].
- [math]\displaystyle{ \,\mathbb{D} }[/math] :- Conditional Covariance Operators and Condtional Indpendence
Let [math]\displaystyle{ \,(H_{11}, k_{11}) }[/math], [math]\displaystyle{ \,(H_{12},k_{12}) }[/math] and [math]\displaystyle{ \,(H_2, k_2) }[/math] be RKHS on measurable space
[math]\displaystyle{ \,\Omega_{11} }[/math], [math]\displaystyle{ \,\Omega_{12} }[/math] and [math]\displaystyle{ \,\Omega_2 }[/math], respectively, with continuous and bounded kernels.
Let [math]\displaystyle{ \,(X,Y)=(U,V,Y) }[/math] be a random vector on [math]\displaystyle{ \,\Omega_{11}\times \Omega_{12} \times \Omega_{2} }[/math], where [math]\displaystyle{ \,X = (U,V) }[/math], and let [math]\displaystyle{ \,H_1 = H_{11} \otimes H_{12} }[/math] be the dirct product. It is assume that [math]\displaystyle{ \,\mathbb{E}_{Y|U} [g(Y)|U= \cdot] \in H_{11} }[/math] and [math]\displaystyle{ \,\mathbb{E}_{Y|X} [g(Y)|X= \cdot] \in H_{1} }[/math] for all [math]\displaystyle{ \,g \in H_2 }[/math]. Then we have
[math]\displaystyle{ \,\Sigma_{YY|U} \ge \Sigma_{YY|X} }[/math],
where the inequality refers to the order of self-adjoint operators.
Furthermore, if [math]\displaystyle{ \,H_2 }[/math] is probability-deremining,
[math]\displaystyle{ \,\Sigma_{YY|X} = \Sigma_{YY|U} \Leftrightarrow Y \perp X|U }[/math].
Therefore, the effective subspace S can be found by minimizing the following function:
[math]\displaystyle{ \,\min_S\quad \Sigma_{YY|U} }[/math],[math]\displaystyle{ \,s.t. \quad U = \Pi_S X }[/math].
Note here for
[math]\displaystyle{ \,\Sigma_{YY|U} \ge \Sigma_{YY|X} }[/math],
in the sense of operator, the inequality means the variance of [math]\displaystyle{ \, Y }[/math] given data [math]\displaystyle{ \, U }[/math] is bigger than the variance of [math]\displaystyle{ \, Y }[/math] given data [math]\displaystyle{ \, X }[/math], which makes sense that [math]\displaystyle{ \, U }[/math] is just a part of the whole data [math]\displaystyle{ \, X }[/math].
- [math]\displaystyle{ \,\mathbb{D} }[/math] :- Stiefel Manifold
Let [math]\displaystyle{ \,M (m \times n;\mathbb{R}) }[/math] be the set of real-valued [math]\displaystyle{ \,\,m \times n }[/math] matrices. For a natural number [math]\displaystyle{ \,d \leq m }[/math], the Stiefel manifold [math]\displaystyle{ \,\mathbb{S}_{d}^{m}(\mathbb{R}) }[/math] is defined by
[math]\displaystyle{ \,\mathbb{S}_{d}^{m}(\mathbb{R}) = \{B \in M(m \times d;\mathbb{R}) | B^T B = I_d \} }[/math]
which is the set of all d orthonormal vectors in [math]\displaystyle{ \,\mathbb{R}^m }[/math]. It is well known that [math]\displaystyle{ \,\mathbb{S}_{d}^{m}(\mathbb{R}) }[/math] is a compact smooth manifold. For [math]\displaystyle{ \,B \in \mathbb{S}_{d}^{m}(\mathbb{R}) }[/math], the matrix [math]\displaystyle{ \,B B^T }[/math] defines an orthogonal projection of [math]\displaystyle{ \,\mathbb{R}^m }[/math] onto the d-dimensional subspace spanned by the column vectors of [math]\displaystyle{ \,B }[/math].
Now that we have defined cross-covariance operators, we are finally ready to link the cross covariance operators to the central subspace. Consider any subspace [math]\displaystyle{ \,S \in X }[/math]. Then we can map this subspace to a RKHS [math]\displaystyle{ \,H_S }[/math] with a kernel function [math]\displaystyle{ \,K_S }[/math]. Furthermore, we define the conditional cross covariance operator as [math]\displaystyle{ \,\Sigma_{YY|S} }[/math] as if we were to regress [math]\displaystyle{ \,Y }[/math] on [math]\displaystyle{ \,S }[/math]. Then, intuitively, the residual error from [math]\displaystyle{ \,\Sigma_{YY|S} }[/math] should be greater than that from [math]\displaystyle{ \,\Sigma_{YY|S} }[/math]. Fukumizu etl al. (2006) formalized that it would be trues unless [math]\displaystyle{ \,S }[/math] contains the central subspace. The intuition is formalized in the following theorem.
[math]\displaystyle{ \, \mathfrak{Theorem 1:-} }[/math] Suppose [math]\displaystyle{ \,Z = B^T B X \in S }[/math] where [math]\displaystyle{ \,B \in \mathbb{R}^{D \times d} }[/math] is a projection matrix such that [math]\displaystyle{ \, B^T B }[/math] is an identity matrix. Further assume Gaussian RBF kernels for [math]\displaystyle{ \, K_X, K_Y, and K_S }[/math]. Then
- [math]\displaystyle{ \,\Sigma_{YY|X} \prec \Sigma_{YY|Z} }[/math] where [math]\displaystyle{ \,\prec }[/math] stands for "less than or equal to" in some operator partial ordering.
- [math]\displaystyle{ \,\Sigma_{YY|X} = \Sigma_{YY|Z} }[/math] if and only if [math]\displaystyle{ \,Y \bot (X - B^T X)|B^T X }[/math], that is, [math]\displaystyle{ \,S }[/math] is a central subspace.
One thing to note about the theorem specifically is that it doesn't impose any strong assumptions on the distribution of X, Y or their marginal distribution [math]\displaystyle{ \,\mathbb{P} }[/math](Y|X) (See Fukumizu et. al. 2006). This theorem leads to the new algorithm for estimating the central subspace characterized by B. Let [math]\displaystyle{ \,\{x_i,y_i\}_{i=1}^{N} }[/math] denote the N samples from the joint distribution of [math]\displaystyle{ \,\mathbb{P} }[/math](X, Y) and let [math]\displaystyle{ \,K_Y \in \mathbb{R}^{N \times N} }[/math] and [math]\displaystyle{ \,K_Z \in \mathbb{R}^{N \times N} }[/math] denote the Gram matrices comuted over yi and zi = BT xi}. Then Fukumizu et al. (2006) <ref>Fukumizu, K., Bach, F. R., & Jordan, M. I. (2006). Kernel dimension reduction in regression (Technical Report). Department of Statistics, University of California, Berkeley.</ref> show that, since X and Y are subsets of Euclidean spaces and Gaussian RBF kernels are used for [math]\displaystyle{ \,K_Y^C }[/math] and [math]\displaystyle{ \,K_Z^C }[/math] (see below), under some conditions the subset B is characterized by the set of solutions of an optimization problem
[math]\displaystyle{ \, B_d^M = \arg_{B \in \mathbb{S}^M_d} \min \Sigma_{YY|X} }[/math]
We can use the Trace to evaluate the partial order of the self-adjoint operators. Thus the Operator [math]\displaystyle{ \,\Sigma_{YY|X}^{B} }[/math] is the trace class for all [math]\displaystyle{ \,B \in \mathbb{S}_d^m(\mathbb{R}) }[/math] by [math]\displaystyle{ \,\Sigma_{YY|X}^{B} \leq \Sigma_{YY} }[/math]. Thus, the above equation can be rewritten as
[math]\displaystyle{ \, \min Tr[\Sigma_{YY|X}^{B}] }[/math]
This problem can be formulated in terms of [math]\displaystyle{ \,K_Y }[/math] and [math]\displaystyle{ \,K_Z }[/math], such that [math]\displaystyle{ \,B }[/math] is the solution to
[math]\displaystyle{ \, \min Tr \mathbb{[}K_Y^C(K_Z^C + N \in I^{-1}) \mathbb{]} }[/math] such that [math]\displaystyle{ \,B^T B = I }[/math]
where I is the Identity matrix and [math]\displaystyle{ \,\epsilon }[/math] is a regularization coefficient. The matrix KC denotes the centered kernel matrices
[math]\displaystyle{ \,K^c = \left(I - \frac{1}{N}ee^T \right) K\left(I - \frac{1}{N}ee^T \right) }[/math]
where e is a vector of all ones.
Manifold Learning
Let [math]\displaystyle{ \,\{x_i,y_i\}_{i=1}^{N} }[/math] denote N data points sampled from the submanifold. Laplacian eigenmaps also appeal to a simple geometric intuition: namely, that nearby high dimensional inputs should be mapped to nearby low dimensional outputs. To this end, a positive weight Wij is associated with inputs xi and xj if either input is among the other’s k-nearest neighbors. Usually, the values of the weights are either chosen to be constant, say Wij = 1/k, or exponentially decaying, as [math]\displaystyle{ \,W_{ij} = exp \left(\frac{- \|x_i - x_j \|^2}{\sigma^2}\right) }[/math]. Let D denote the diagonal matrix with elements [math]\displaystyle{ \, D_{ii} = \sum_{\forall j}W_{ij} }[/math]. Then the outputs yi can be chosen such that it minimizes the cost function:
[math]\displaystyle{ \,\Psi(Y) = \sum_{\forall ij} \frac{W_ij\|y_i - y_j \|^2}{\sqrt{D_{ii}D_{jj}}} }[/math] (6)
The embedding is computed from the bottom eigenvectors of the matrix [math]\displaystyle{ \,\Psi = I - D^{- \frac{1}{2}} W D^{- \frac{1}{2}} }[/math] where the matrix [math]\displaystyle{ \,\Psi }[/math] is a symmetrized, normalized form of the graph Laplacian, given by D - W.
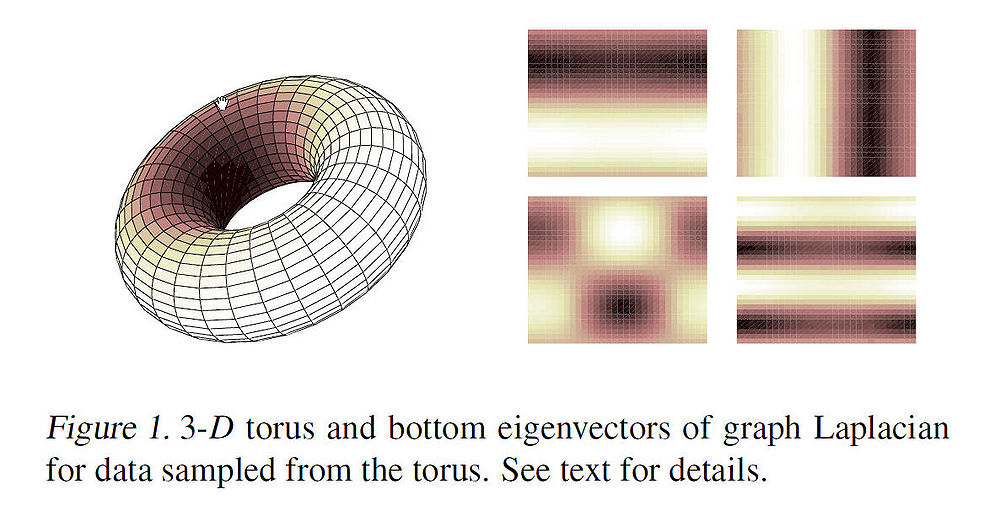
As an example, the figure below shows some of the first non-constant eigenvectors (mapped onto 2-D) for data points sampled from a 3-D torus. The image intesities correspond to high and low values of the eigen vectors. The variation in the intensities can be interpreted as the high and low frequency components of the harmonic functions. Intuitively, these eigenvectors can be used to approximate smooth functions on the manifold.
Manifold Kernel Dimension Reduction
The new algorithm introduced by the authors is called Manifold Kernal Dimension Reduction (mKDR) which combines ideas from supervised manifold learning and Kernel Dimension Reduction.
In essence the algorithm is has three main elements:
(1) Compute a Low-Dimension embedding of the covariates X; (2) Parametrize the central subspace as a linear transformation of the lower-dimensional embedding; (3) Compute the coefficients of the optimal linear map using the Kernel Dimension Reduction framework
The linear map achieved from the algorithm yields directions in the low-dimensional embedding that contribute most significantly to the central subspace. the authors start by illustrating the derivation of the algorithm and then outline the mKDR algorithm.
Derivation
For an M-Dimensional embedding [math]\displaystyle{ \,U \in \mathcal{U} \subset \mathbb{R}^{M \times N} }[/math] generated by graph laplacian, choose M eigenvectors [math]\displaystyle{ \,\{v_m\}_{m=1}^{M} }[/math] (see below for a choice of M).Then continuing from the KDR framework, consider a Kernel function that maps a point BTxi in the central subspace to the Reproducing Kernel Hilbert Space (RKHS). Construct the mapping K(;) as
[math]\displaystyle{ \,K \left(; B^T x_i \right) \approx \Phi u_i }[/math]
where [math]\displaystyle{ \,\,\Phi u_i }[/math] is a linear expression approximating the Kernel Function. Note that, [math]\displaystyle{ \,\Phi \in \mathbb{R}^{M \times M} }[/math] is a linear map independent of xi and our aim now is to find [math]\displaystyle{ \,\Phi }[/math]. This can be done through the KDR framework by minimizing the cost function [[Tr [math]\displaystyle{ \,\mathbb{[} K_Y^C(K_Z^C + N \in I) \mathbb{]} }[/math]]] for statistical independence between yi and xi. Then the Gram Matrix is approximated and parametrized by the linear map [math]\displaystyle{ \,\,\Phi }[/math] i.e.
[math]\displaystyle{ \,\lt K(;B^T x_i),K(B^T x_j)\gt \approx u_i^T \Phi^T \Phi u_j }[/math]
Define [math]\displaystyle{ \,\,\Omega = \Phi^T \Phi }[/math]. Then, continuing from the earlier minimization problem, the matrix KCZ can be approximated by
[math]\displaystyle{ \, K_Z^C \approx U^T \Omega U }[/math]
which allows us to formulate the problem as
Minimize: [math]\displaystyle{ \,\,Tr \mathcal{[} K^C_Y(U^T \Omega U + N \epsilon I)^-1 \mathcal{]} }[/math]
Such that: [math]\displaystyle{ \,\,\Omega \succeq 0 }[/math]
- [math]\displaystyle{ \,\,Tr(\Omega)= 1 }[/math]
The above optimization problem is nonlinear and nonconvex. The second constraint of unit trace is added becuase the objective function attains arbitrarily small value with infimum of zero if [math]\displaystyle{ \,\Omega }[/math] grows arbitrarily large. Furthermore, the matrix [math]\displaystyle{ \,\,\Omega }[/math] needs to be constrained in the cone of positive semidefinitive matrices i.e. [math]\displaystyle{ \,\Omega \succeq 0 }[/math] in order to compute the linear map [math]\displaystyle{ \,\,\Phi }[/math] as the square root of [math]\displaystyle{ \,\,\Omega }[/math].
Once we get our linear map, we can find the matrix B inverting the map that we initially constructed (i.e. [math]\displaystyle{ \,\,K \left(; B^T x_i \right) \approx \Phi u_i }[/math]). The authors did point out however, that in case of regression using reduced dimensionality it is sufficient to regress Y on the central subspace[math]\displaystyle{ \,\,\Phi U }[/math].
The problem of choosing dimensionality is an open problem in case of KDR. One suggested strategy is to choose M relatively larger than a conservative prior estimate d of the central subspace. In this situation, we hope/rely on the fact that the solution to the above described optimization problem leads to a low rank of the linear map [math]\displaystyle{ \,\,\Phi }[/math]. Thus, r = RANK([math]\displaystyle{ \,\,\Phi }[/math]) provides an emperical estimate of d. Thus, if we let [math]\displaystyle{ \,\,\Phi^r }[/math] denote the matrix formed by the rop r eigenvectors of [math]\displaystyle{ \,\,\Phi }[/math], then the subspace [math]\displaystyle{ \,\,\Phi U }[/math] can be approximated with [math]\displaystyle{ \,\,\Phi^r U }[/math]. Furthermore, the row vectors of the matrix [math]\displaystyle{ \,\,\Phi^r }[/math] are combinations of Eigenfunctions. Using the Eigen functions with the largest coefficients, we can visualize the original data {xi}
Algorithm
Note that that the authors applied the projected gradient descent method in the algorithm to find the local optimal minimizers. As illustrated in the next section, the authors claim that it worked well for the experimental data. Furthermore, despite the problem being nonconvex, initialization with the identity matrix gave fast convergence in experiments.
Experimental Results
The authors illustrate the effectiveness of the MKDR algorithm by applying their algorithm to one artificial data set and two real world data sets. The following examples illustrate the potential and shortcomings of the algorithm for exploratory data analysis and visualization of high-dimensional data.
Regression on Torus
In this section we analyze data points lying on the surface of a torus, illustrated below in Fig. 1. A torus can be constructed by rotating a 2-D cycle in [math]\displaystyle{ \,\, \mathbb{R}^3 }[/math] with respect to an axis. Thus, a data point on the surface has two degrees of freedom: the rotated angle [math]\displaystyle{ \,\,\theta_r }[/math] with respect to the axis and the polar angle [math]\displaystyle{ \,\, \theta_p }[/math] on the cycle. The synthesized data set is formed by sampling these two angles from the Cartesian product [math]\displaystyle{ \,\, [0 2\pi] \times [0 2\pi] }[/math]. As a result of that the 3-D coordinates of our torus will be [math]\displaystyle{ \,\, \mathbf{x_1=(2+cos\theta_r)cos\theta_p, x_2=(2+cos\theta_r)sin\theta_p} }[/math] and [math]\displaystyle{ \,\, \mathbf{x_3=sin\theta_r} }[/math]. After that the torus can be embeded in [math]\displaystyle{ \,\, \mathbf{x \in R^{10}} }[/math] by augmenting the coordinates with 7-dimensional all-zero or random vectors. For setting up the regression problem, we define the response by [math]\displaystyle{ \,\, \mathbf{y=\sigma[-17(\sqrt((\theta_r-\pi)^2+(\theta_p-\pi)^2)-0.6\pi)]} }[/math] where [math]\displaystyle{ \,\, \sigma[.] }[/math] is the sigmoid function. The colors on the surface of the torus in Fig. 1 correspond to the value of the response.
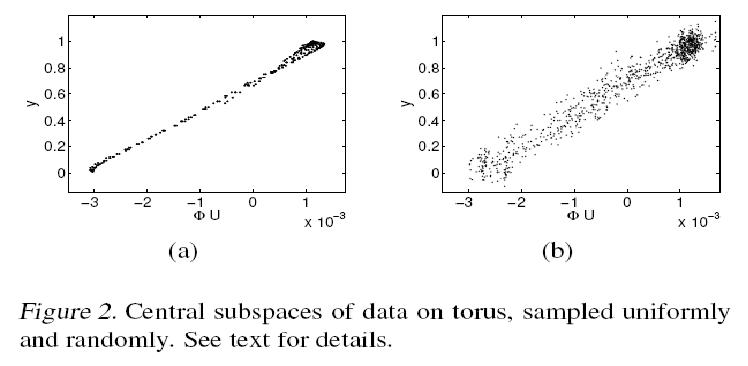
The mKDR was applied to the torus data set generated from 961 uniformly sampled angles [math]\displaystyle{ \,\, \theta_p }[/math] and [math]\displaystyle{ \,\, \theta_r }[/math] and [math]\displaystyle{ \,\, M = 50 }[/math] bottom eigenvectors from the graph Laplacian were used. The mKDR algorithm then computed the matrix [math]\displaystyle{ \,\, \mathbf{ \Phi \in R^{50 \times 50}} }[/math] that minimizes the empirical conditional covariance operator; This matrix turned out to be of nearly rank 1 and can be approximated by [math]\displaystyle{ \, \mathbf{a^T a} }[/math] where [math]\displaystyle{ \, \mathbf{a} }[/math] is the eigenvector corresponding to the largest eigenvalue. Hence, the 50-D embedding of the graph Laplacian was projected onto this principal direction [math]\displaystyle{ \,\, \mathbf{a} }[/math].
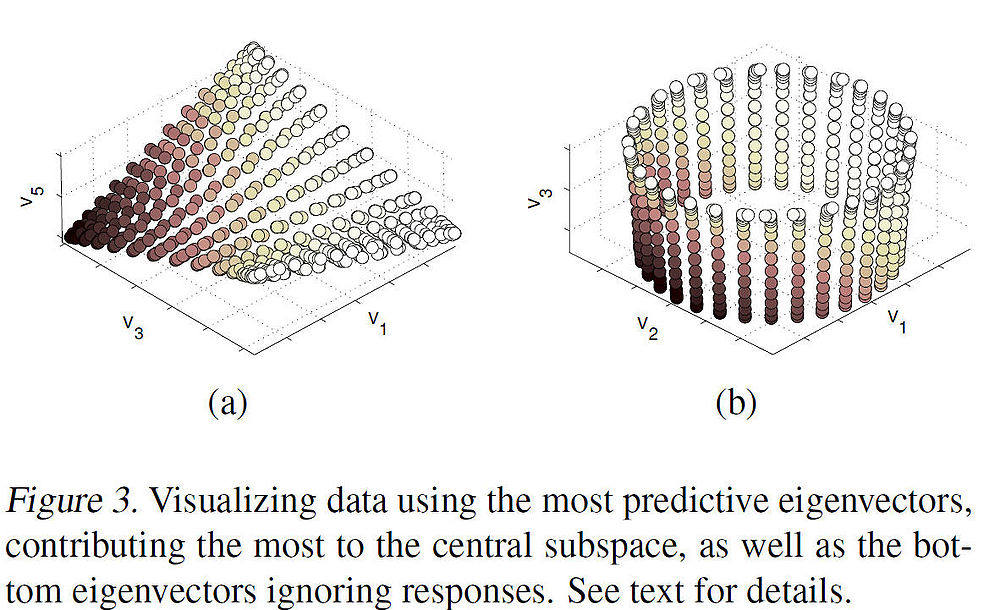
The principal direction [math]\displaystyle{ \,\, \mathbf{a} }[/math] allows us to view the central subspaces in RKHS induced by the manifold learning kernel. More specifically, [math]\displaystyle{ \,\, \mathbf{a} }[/math] encodes the combining coefficients of eigenvectors. Figure 3(a) below shows the 3-D embedding of samples using the predictive eigenvectors (i.e. the eigenvectors most useful in forming the principal direction) as coordinates, where the color encodes the responses. Figure 3(b) shows the 3-D embedding of the torus using the bottom 3 eigenvectors. The purpose of the contrast is to illustrate how data is visualization is clear under mKDR as it arranges samples under the guidance of the responses while unsupervised graph Laplacian does so solely based on the intrinsic geometry of the covariates.
Predicting Global Temperature
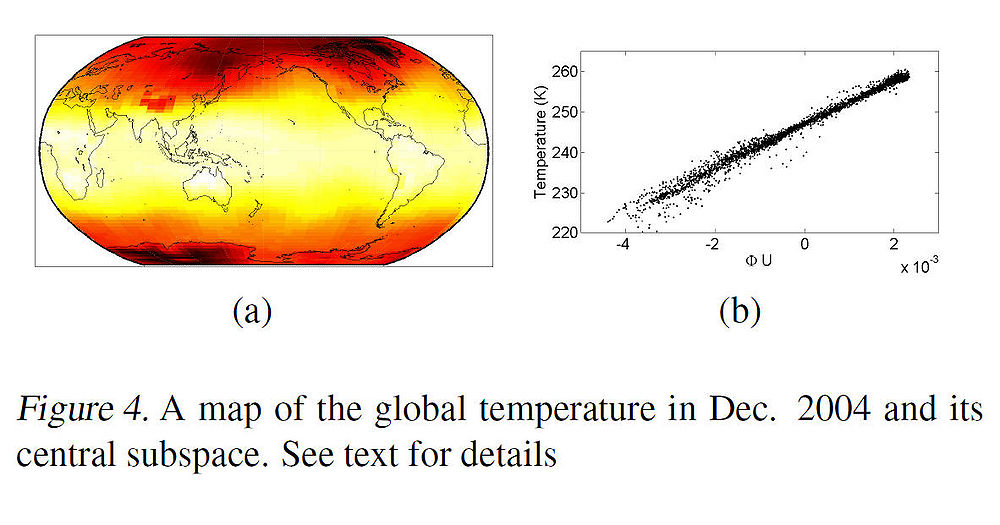
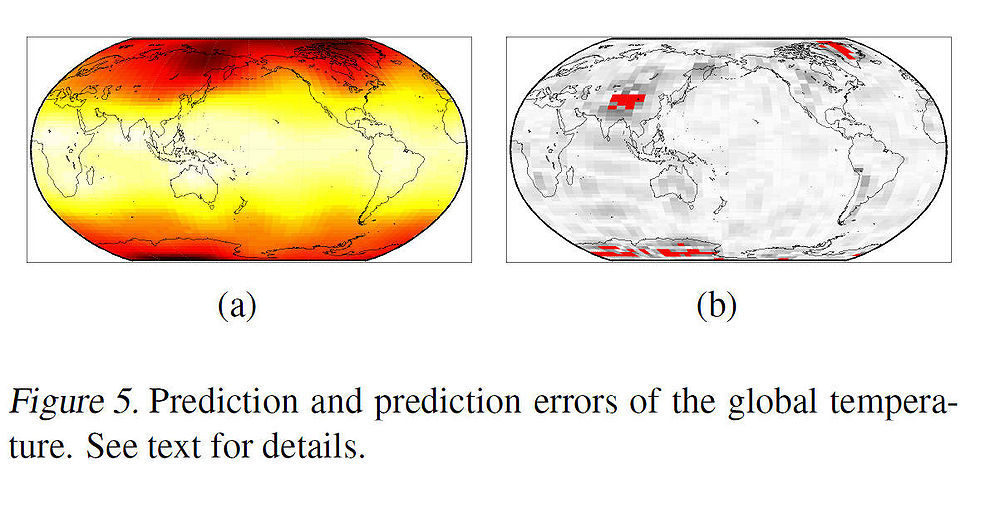
To illustrate the effectiveness of the proposed algorithm, the authors applied it to global temperature data. Figure 4 below shows a map of global temperature in Dec. 2004 which is encoded by colors where yellow or white colors mean hotter temperature and red colors mean lower temperature. The regression problem was to predict the temperature using only two covariates i.e. latitude and longitude.
Note that the domain of the covariates is not Euclidean, but rather ellipsoidal (and thus, the problem is complex nonlinear regression problem). After projecting the M-dimensional manifold embedding (where M was chosen to be 100) onto the principal direction of the linear map [math]\displaystyle{ \,\,\Phi }[/math], we can see from the scatter plot in Fig. 4(b) that the projection against the temperatures has a relatively linear relationship. Linearity was tested by regressing the temperatures on the projections, using a linear regression function. Fig. 5(a) and Fig. 5(b) show the predicted temperatures and the prediction errors (in red) respectively.
The above example illustrates the effectiveness of the mKDR algorithm as the central space predicts the overall temperature pattern well.
Regression on Image Manifolds
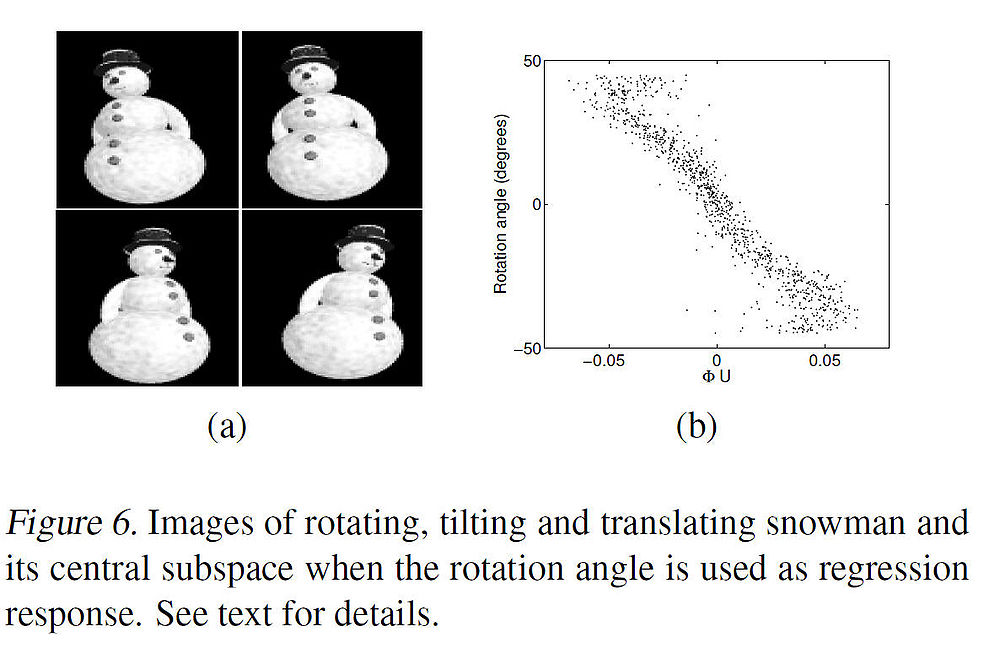
To illustrate the effectiveness of the algorithm on a high dimensional data set, the authors illustrated it by experimenting with a real-world data set whose underlying manifold is high-dimensional and unknown. The data set consists of one thousand 110[math]\displaystyle{ \,\,110\times 80 }[/math] images of a snowman in a three-dimensional scene. First, snowman picture is rotated around its axis with an angle chosen uniformly random from the interval [math]\displaystyle{ \,\,[−45^{\circ}, 45^{\circ}] }[/math], and then tilted with an angle chosen uniformly random from [math]\displaystyle{ \,\,[−10^{\circ}, 10^{\circ}] }[/math]. Further, the objects are subject to random vertical plane translations spanning 5 pixels in each direction (thus, all variations are chosen independently). A few representative images of such variations are shown below in Fig. 6(a).
Suppose that we would like to create a low-dimensional embedding of the data that highlights the angle of rotation of the image variation, while also maintaining variations in other factors. This is set up as a regression problem whose covariates are image pixel intensities and whose responses are the rotation angles of the images. Again, choosing M eigenvectors (for M = 100), the mKDR algorithm is applied to the data set which returned a central subspace whose first direction correlates fairly well with the rotation angle, as shown above in Fig. 6(b).
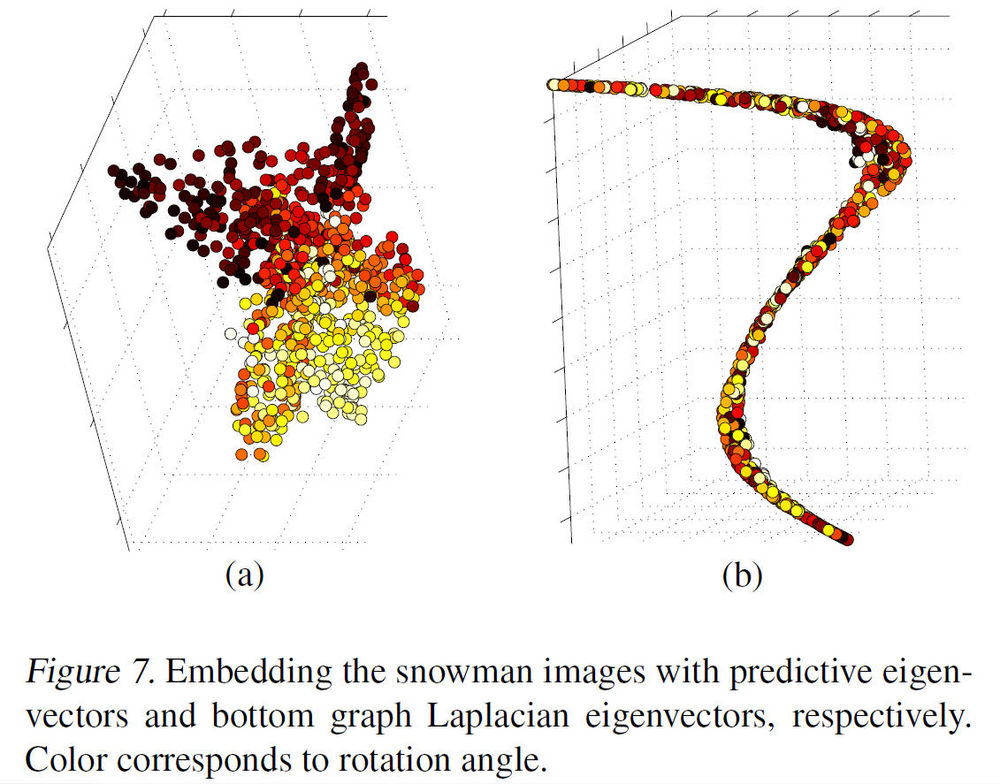
In Fig. 7(a) below, the data is visualized in [math]\displaystyle{ \,\,\mathbb{R}^3 }[/math] by using the top three predictive eigenvectors (i.e. eigenvectors which were most useful in forming the principal direction) and it shows that the data clustering pattern in the rotation angles are clearly present. Compared with choosing the bottom three eigenvectors as shown in Fig. 7(b) with colors encoding, i.e. the rotation angles, shows no clear structure or pattern, in terms of rotation. In fact, the nearly one-dimensional embedding reflects closely the tilt angle, which tends to cause large variations in image pixel intensities.
Further Research
This paper presented a new algorithm for dimensionality reduction that is appropriate when supervised information is available. The algorithm stands out not only because of its higher predictive power, but also because it combines the ideas from two strands of research i.e. Sufficient Dimension Reduction from Statistics and Manifold Learning from the Machine Learning literature. The ideas from two diverse fields is essentially connected by the ideas proposed in the methodology of Kernel Dimension Reduction.
As illustrated in the examples above, the algorithm finds a lower dimension and predictive subspaces and revealed some interesting patterns. Overall, the mKDR algorithm is a particular instantiation of the framework of kernel dimension reduction. Thus, it inherits all the advantages of the kernel methods in general, including the abuility to handle multivariate response variables and non-vectorial data.
References
<references/>