PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space
Introduction
This paper builds off of ideas from PointNet (Qi et al., 2017). The name PointNet is derived from the network's input - a point cloud. A point cloud is a set of three dimensional points that each have coordinates [math]\displaystyle{ (x,y,z) }[/math]. These coordinates usually represent the surface of an object. For example, a point cloud describing the shape of a torus is shown below.

Processing point clouds is important in applications such as autonomous driving where point clouds are collected from an onboard LiDAR sensor. These point clouds can then be used for object detection. However, point clouds are challenging to process because:
- They are unordered. If [math]\displaystyle{ N }[/math] is the number of points in a point cloud, then there are [math]\displaystyle{ N! }[/math] permutations that the point cloud can be represented.
- The spatial arrangement of the points contains useful information, thus it needs to be encoded.
- The function processing the point cloud needs to be invariant to transformations such as rotation and translations of all points.
Previously, typical point cloud processing methods handled the challenges of point clouds by transforming the data with a 3D voxel grid or by representing the point cloud with multiple 2D images. When PointNet was introduced, it was novel because it directly took points as its input. PointNet++ improves on PointNet by using a hierarchical method to better capture local structures of the point cloud.

Review of PointNet
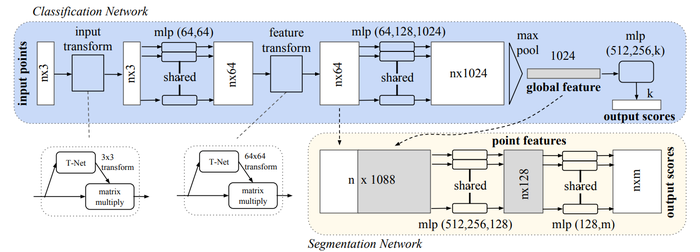
The PointNet architecture is shown below. The input of the network is [math]\displaystyle{ n }[/math] points, which each have [math]\displaystyle{ (x,y,z) }[/math] coordinates. Each point processed individually through a multi-layer perceptron (MLP). This network creates an encoding for each point; in the diagram, each point is represented by a 1024 dimension vector. Then, using a max pool layer a vector is created, that represents the "global signature" of a point cloud. If classification is the task, this global signature is processed by another MLP to compute the classification scores. If segmentation is the task, this global signature is appended to to each point from the "nx64" layer, and these points are processed by a MLP to compute a semantic category score for each point.
The core idea of the network is to learn a symmetric function on transformed points. Through the T-Nets and the MLP network, a transformation is learned with the hopes of making points invariant to point cloud transformations. Learning a symmetric function solves the challenge imposed by having unordered points; a symmetric function will produce the same value no matter the order of the input. This symmetric function is represented by the max pool layer.
PointNet++
The motivation for PointNet++ is that PointNet does not capture local, fine-grained details. Since PointNet performs a max pool layer over all of its points, information such as the local interaction between points is lost.
Problem Statement
There is a metric space [math]\displaystyle{ X = (M,d) }[/math] where [math]\displaystyle{ d }[/math] is the metric from a Euclidean space [math]\displaystyle{ \pmb{\mathbb{R}}^n }[/math] and [math]\displaystyle{ M \subseteq \pmb{\mathbb{R}}^n }[/math] is the set of points. The goal is to learn a function that takes [math]\displaystyle{ X }[/math] as the input as outputs a a class or per point label to each member of [math]\displaystyle{ M }[/math].
Method
High Level Overview
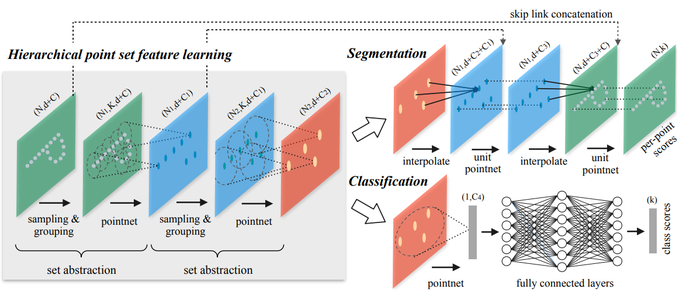
The PointNet++ architecture is shown on the right. The core idea is that a hierarchical architecture is used and at each level of the hierarchy a set of points is processed and abstracted to a new set with less points, i.e.,
\begin{aligned} \text{Input at each level: } N \times (d + c) \text{ matrix} \end{aligned}
where [math]\displaystyle{ N }[/math] is the number of points, [math]\displaystyle{ d }[/math] is the coordinate points [math]\displaystyle{ (x,y,z) }[/math] and [math]\displaystyle{ c }[/math] is the feature representation of each point, and
\begin{aligned} \text{Output at each level: } N' \times (d + c') \text{ matrix} \end{aligned}
where [math]\displaystyle{ N' }[/math] is the new number (smaller) of points and [math]\displaystyle{ c' }[/math] is the new feature vector.
Each level has three layers: Sampling, Grouping, and PointNet. The Sampling layer selects points that will act as centroids of local regions within the point cloud. The Grouping layer then finds points near these centroids. Lastly, the PointNet layer performs PointNet on each group to encode local information.
Sampling Layer
The input of this layer is a set of points [math]\displaystyle{ {\{x_1,x_2,...,x_n}\} }[/math]. The goal of this layer is to select a subset of these points [math]\displaystyle{ {\{\hat{x}_1, \hat{x}_2,...,\hat{x}_m\}} }[/math] that will define the centroid of local regions.
To select these points farthest point sampling is used. This is where [math]\displaystyle{ \hat{x}_j }[/math] is the most distant point with regards to [math]\displaystyle{ {\{\hat{x}_1, \hat{x}_2,...,\hat{x}_{j-1}\}} }[/math]. This ensures coverage of the entire point cloud opposed to random sampling.
Grouping Layer
PointNet Layer
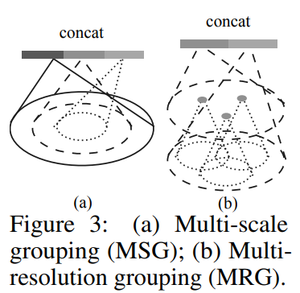
Robust Feature Learning under Non-Uniform Sampling Density
Experiments
Sources
1. Charles R. Qi, Li Yi, Hao Su, Leonidas J. Guibas. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space, 2017
2. Charles R. Qi, Hao Su, Kaichun Mo, Leonidas J. Guibas. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation, 2017