PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space: Difference between revisions
No edit summary |
|||
| Line 84: | Line 84: | ||
[[File:grouping.png | 300px|thumb|center|Example of the two ways to perform grouping]] | [[File:grouping.png | 300px|thumb|center|Example of the two ways to perform grouping]] | ||
== Network Architectures == | |||
=== all classification experiments with K categories === | |||
SA(512, 0.2, [64, 64, 128]) → SA(128, 0.4, [128, 128, 256]) → SA([256, 512, 1024]) → F C(512, 0.5) → F C(256, 0.5) → F C(K) | |||
=== The multi-scale grouping (MSG) network === | |||
SA(512, [0.1, 0.2, 0.4], [[32, 32, 64], [64, 64, 128], [64, 96, 128]]) → SA(128, [0.2, 0.4, 0.8], [[64, 64, 128], [128, 128, 256], [128, 128, 256]]) → SA([256, 512, 1024]) → F C(512, 0.5) → F C(256, 0.5) → F C(K) | |||
=== The cross level multi-resolution grouping (MRG) network === | |||
Branch 1: SA(512, 0.2, [64, 64, 128]) → SA(64, 0.4, [128, 128, 256]) | |||
Branch 2: SA(512, 0.4, [64, 128, 256]) using r = 0.4 regions of original points | |||
Branch 3: SA(64, 128, 256, 512) using all original points. | |||
Branch 4: SA(256, 512, 1024). | |||
== Point Cloud Segmentation == | == Point Cloud Segmentation == | ||
Latest revision as of 22:59, 20 April 2018
Introduction
This paper builds off of ideas from PointNet (Qi et al., 2017). The name PointNet is derived from the network's input - a point cloud. A point cloud is a set of three dimensional points that each have coordinates [math]\displaystyle{ (x,y,z) }[/math]. These coordinates usually represent the surface of an object. For example, a point cloud describing the shape of a torus is shown below.

Processing point clouds is important in applications such as autonomous driving where point clouds are collected from an onboard LiDAR sensor. These point clouds can then be used for object detection. However, point clouds are challenging to process because:
- They are unordered. If [math]\displaystyle{ N }[/math] is the number of points in a point cloud, then there are [math]\displaystyle{ N! }[/math] permutations that the point cloud can be represented.
- The spatial arrangement of the points contains useful information, thus it needs to be encoded.
- The function processing the point cloud needs to be invariant to transformations such as rotation and translations of all points.
Previously, typical point cloud processing methods handled the challenges of point clouds by transforming the data with a 3D voxel grid or by representing the point cloud with multiple 2D images. When PointNet was introduced, it was novel because it directly took points as its input. PointNet++ improves on PointNet by using a hierarchical method to better capture local structures of the point cloud.

Related Work
This paper provides a new network to understand point clouds. CNNs are the most prominent deep networks which find features in images/videos. However, the convolution process is not applicable to point clouds as point clouds contain unordered set of points with distance metric. Some techniques apply deep learning to unordered sets however they don't account for the distance metric in their model and are sensitive to translation and global normalization. Techniques like volumetric grids and geometric graphs work on the 3D metric space but the problem of non-uniform sampling density hasn't been considered.
Review of PointNet
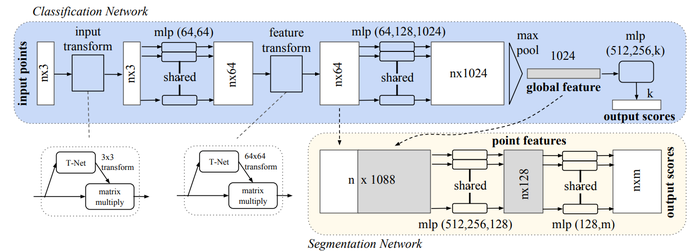
The PointNet architecture is shown below. The input of the network is [math]\displaystyle{ n }[/math] points, which each have [math]\displaystyle{ (x,y,z) }[/math] coordinates. Each point is processed individually through a multi-layer perceptron (MLP). This network creates an encoding for each point; in the diagram, each point is represented by a 1024 dimension vector. Then, using a max pool layer a vector is created that represents the "global signature" of a point cloud. If classification is the task, this global signature is processed by another MLP to compute the classification scores. If segmentation is the task, this global signature is appended to to each point from the "nx64" layer, and these points are processed by a MLP to compute a semantic category score for each point.
The core idea of the network is to learn a symmetric function on transformed points. Through the T-Nets and the MLP network, a transformation is learned with the hopes of making points invariant to point cloud transformations. Learning a symmetric function solves the challenge imposed by having unordered points; a symmetric function will produce the same value no matter the order of the input. This symmetric function is represented by the max pool layer.
PointNet++
The motivation for PointNet++ is that PointNet does not capture local, fine-grained details. Since PointNet performs a max pool layer over all of its points, information such as the local interaction between points is lost. Max-pooling reduces the dimensionality of the network in a very cheap way (with no parameters), but is only good some tasks since it only provides translatioinal variance. And by translational variance we mean that the same object with slightly change in orientation or posiution might not fire up the neuron that is supposed to recognize that object.
Problem Statement
There is a metric space [math]\displaystyle{ X = (M,d) }[/math] where [math]\displaystyle{ d }[/math] is the metric from a Euclidean space [math]\displaystyle{ \pmb{\mathbb{R}}^n }[/math] and [math]\displaystyle{ M \subseteq \pmb{\mathbb{R}}^n }[/math] is the set of points. The goal is to learn functions [math]\displaystyle{ f }[/math] that take [math]\displaystyle{ X }[/math] as the input and produce information of semantic interest about it. In practice, [math]\displaystyle{ f }[/math] can often be a classification function that outputs a class label or a segmentation function that outputs a per point label for each member of [math]\displaystyle{ M }[/math].
Method
High Level Overview
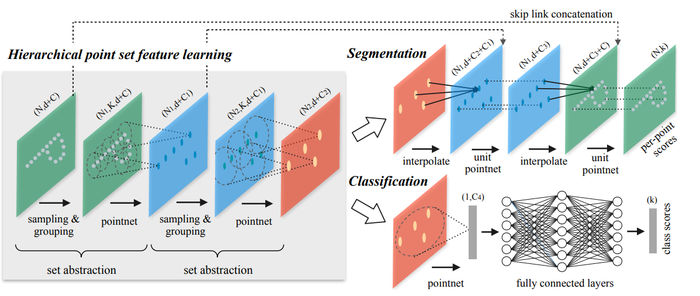
The PointNet++ architecture is shown on the right. The core idea is that a hierarchical architecture is used and at each level of the hierarchy a set of points is processed and abstracted to a new set with less points, i.e.,
\begin{aligned} \text{Input at each level: } N \times (d + c) \text{ matrix} \end{aligned}
where [math]\displaystyle{ N }[/math] is the number of points, [math]\displaystyle{ d }[/math] is the coordinate points [math]\displaystyle{ (x,y,z) }[/math] and [math]\displaystyle{ c }[/math] is the feature representation of each point, and
\begin{aligned} \text{Output at each level: } N' \times (d + c') \text{ matrix} \end{aligned}
where [math]\displaystyle{ N' }[/math] is the new number (smaller) of points and [math]\displaystyle{ c' }[/math] is the new feature vector.
Each level has three layers: Sampling, Grouping, and PointNet. The Sampling layer selects points that will act as centroids of local regions within the point cloud. The Grouping layer then finds points near these centroids. Lastly, the PointNet layer performs PointNet on each group to encode local information.
Sampling Layer
The input of this layer is a set of points [math]\displaystyle{ {\{x_1,x_2,...,x_n}\} }[/math]. The goal of this layer is to select a subset of these points [math]\displaystyle{ {\{\hat{x}_1, \hat{x}_2,...,\hat{x}_m\}} }[/math] that will define the centroid of local regions.
To select these points farthest point sampling is used. This is where [math]\displaystyle{ \hat{x}_j }[/math] is the most distant point with regards to [math]\displaystyle{ {\{\hat{x}_1, \hat{x}_2,...,\hat{x}_{j-1}\}} }[/math]. This ensures coverage of the entire point cloud opposed to random sampling.
Grouping Layer
The objective of the grouping layer is to form local regions around each centroid by grouping points near the selected centroids. The input is a point set of size [math]\displaystyle{ N \times (d + c) }[/math] and the coordinates of the centroids [math]\displaystyle{ N' \times d }[/math]. The output is the groups of points within each region [math]\displaystyle{ N' \times k \times (d+c) }[/math] where [math]\displaystyle{ k }[/math] is the number of points in each region.
Note that [math]\displaystyle{ k }[/math] can vary per group. Later, the PointNet layer creates a feature vector that is the same size for all regions at a hierarchical level.
To determine which points belong to a group a ball query is used; all points within a radius of the centroid are grouped. This is advantageous over nearest neighbour because it guarantees a fixed region space, which is important when learning local structure.
PointNet Layer
After grouping, PointNet is applied to the points. However, first the coordinates of points in a local region are converted to a local coordinate frame by [math]\displaystyle{ x_i = x_i - \bar{x} }[/math] where [math]\displaystyle{ \bar{x} }[/math] is the coordinates of the centroid.
Robust Feature Learning under Non-Uniform Sampling Density
The previous description of grouping uses a single scale. This is not optimal because the density varies per section of the point cloud. At each level, it would be better if the PointNet layer was applied to adaptively sized groups depending on the point cloud density.
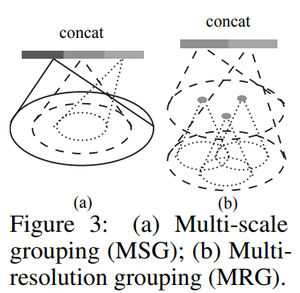
The two grouping methods the authors propose are shown in the diagram below. Multi-scale grouping (MSG) applies PointNet at various scales per group. The features from the various scales are concatenated to form a multi-scale feature. To train the network to learn an optimal strategy for combining the multi-scale features, the authors proposed random input dropout, which involves randomly dropping input points with a random probability for each training point set. Each input point has a dropout probability [math]\displaystyle{ \theta }[/math]. The authors used a [math]\displaystyle{ \theta }[/math] value of 0.95. As shown in the experiments section below, dropout provides robustness to input point density variations. During testing stage all points are used. MSG, however, is computationally expensive because for each region it always applies PointNet at large scale neighborhoods to all points.
On the other hand, multi-resolution grouping (MRG) is less computationally expensive but still adaptively collects features. As shown in the diagram, features of a region from a certain level is a concatenation of two vectors. The left vector is obtained by applying PointNet to three points, and these three points obtained information from three groups. This vector is then concatenated by a vector that is created by using PointNet on all the points in the level below. The second vector can be weighed more heavily if the first vector contains a sparse amount of points, since the first vector is based on subregions that would be even more sparse and suffer from sampling deficiency. On the other hand, when the density of a local region is high, the first vector can be weighted more heavily as it allows for inspecting at higher resolutions in the lower levels to obtain finer details.
Network Architectures
all classification experiments with K categories
SA(512, 0.2, [64, 64, 128]) → SA(128, 0.4, [128, 128, 256]) → SA([256, 512, 1024]) → F C(512, 0.5) → F C(256, 0.5) → F C(K)
The multi-scale grouping (MSG) network
SA(512, [0.1, 0.2, 0.4], [[32, 32, 64], [64, 64, 128], [64, 96, 128]]) → SA(128, [0.2, 0.4, 0.8], [[64, 64, 128], [128, 128, 256], [128, 128, 256]]) → SA([256, 512, 1024]) → F C(512, 0.5) → F C(256, 0.5) → F C(K)
The cross level multi-resolution grouping (MRG) network
Branch 1: SA(512, 0.2, [64, 64, 128]) → SA(64, 0.4, [128, 128, 256]) Branch 2: SA(512, 0.4, [64, 128, 256]) using r = 0.4 regions of original points Branch 3: SA(64, 128, 256, 512) using all original points. Branch 4: SA(256, 512, 1024).
Point Cloud Segmentation
If the task is segmentation, the architecture is slightly modified since we want a semantic score for each point. To achieve this, distance-based interpolation and skip-connections are used.
Distance-based Interpolation
Here, point features from [math]\displaystyle{ N_l \times (d + C) }[/math] points are propagated to [math]\displaystyle{ N_{l-1} \times (d + C) }[/math] points where [math]\displaystyle{ N_{l-1} }[/math] is greater than [math]\displaystyle{ N_l }[/math].
To propagate features an inverse distance weighted average based on [math]\displaystyle{ k }[/math] nearest neighbors is used. The [math]\displaystyle{ p=2 }[/math] and [math]\displaystyle{ k=3 }[/math].
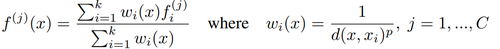
Skip-connections
In addition, skip connections are used (see the PointNet++ architecture diagram). The features from the the skip layers are concatenated with the interpolated features. Next, a "unit-wise" PointNet is applied, which the authors describe as similar to a one-by-one convolution.
Experiments
To validate the effectiveness of PointNet++, experiments in three areas were performed - classification in Euclidean metric space, semantic scene labeling, and classification in non-Euclidean space.
Point Set Classification in Euclidean Metric Space
The digit dataset, MNIST, was converted to a 2D point cloud. Pixel intensities were normalized in the range of [math]\displaystyle{ [0, 1] }[/math], and only pixels with intensities larger than 0.5 were considered. The coordinate system was set at the centre of the image. PointNet++ achieved a classification error of 0.51%. The original PointNet had 0.78% classification error. The table below compares these results to the state-of-the-art.

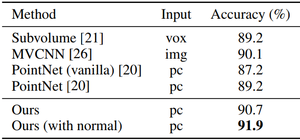
In addition, the ModelNet40 dataset was used. This dataset consists of CAD models. Three dimensional point clouds were sampled from mesh surfaces of the ModelNet40 shapes. The classification results from this dataset are shown below. The last row in the table below, "Ours (with normal)" used face normals (normal is the same for the entire face, regardless of the point picked on that face) as additional point features as well as additional points [math]\displaystyle{ (N = 5000) }[/math] to boost performance. All these points are normalized to have zero mean and be within one unit ball. The network contains three hierarchical levels with three fully connected layers.
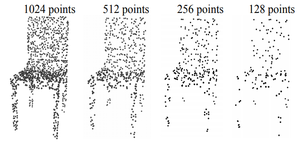
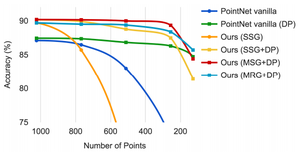
An experiment was performed to show how the accuracy was affected by the number of points used. With PointNet++ using multi-scale grouping and dropout, the performance decreased by less than 1% when 1024 test points were reduced to 256. On the other hand, PointNet's performance was impacted by the decrease in points. This is not surprising because the dropout feature of PointNet++ ensures that the model is trained specifically to be robust to loss of points.
Semantic Scene Labelling
The ScanNet dataset was used for experiments in semantic scene labelling. This dataset consists of laser scans of indoor scenes where the goal is to predict a semantic label for each point. Example results are shown below.
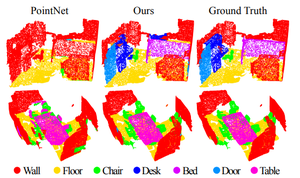
To compare to other methods, the authors convert their point labels to a voxel format, and accuracy is determined on a per voxel basis. The accuracy compared to other methods is shown below.
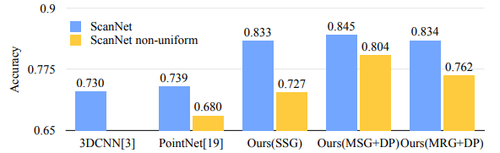
To test how the trained model performed on scans with non-uniform sampling density, virtual scans of ScanNet scenes were synthesized and the network was evaluated on this data. It can be seen from the above figures that SSG performance greatly falls due to the sampling density shift. MRG network, on the other hand, is more robust to the sampling density shift since it is able to automatically switch to features depicting coarser granularity when the sampling is sparse. This proves the effectiveness of the proposed density adaptive layer design.
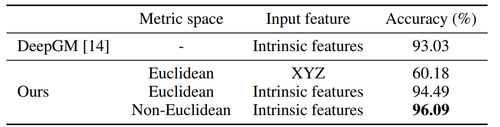
Classification in Non-Euclidean Metric Space
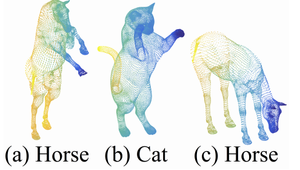
Lastly, experiments were performed on the SHREC15 dataset. This dataset contains shapes that have different poses. This experiment shows that PointNet++ is able to generalize to non-Euclidean spaces. Results from this dataset are provided below.
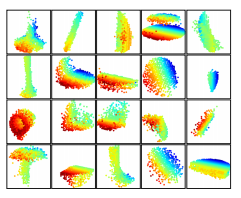
Feature Visualization
The figure below visualizes what is learned by just the first layer kernels of the network. The model is trained on a dataset the mostly consisted of furniture which explains the lines, corners, and planes visible in the visualization. Visualization is performed by creating a voxel grid in space and only aggregating point sets that activate specific neurons the most.
Time and Space Complexity
To evaluate the time and space complexity between PointNet++ and PointNet the authors recorded the model size and inference time for several point set deep learning approaches. Inference time is measured with a GTX 1080 and batch size 8. The PointNet inference times are significantly better however the model sizes for PointNet++ are comparable. The table below outlines the specifics for each method.
Worth noting is that ours MSG, while it has good performance in non-uniformly sampled data, it’s twice as expensive as then SSG version due the multi-scale region feature extraction. Compared with MSG, MRG is more efficient since it uses regions across layers.

Critique
It seems clear that PointNet is lacking capturing local context between points. PointNet++ seems to be an important extension, but the improvements in the experimental results seem small. Some computational efficiency experiments would have been nice. For example, the processing speed of the network, and the computational efficiency of MRG over MRG.
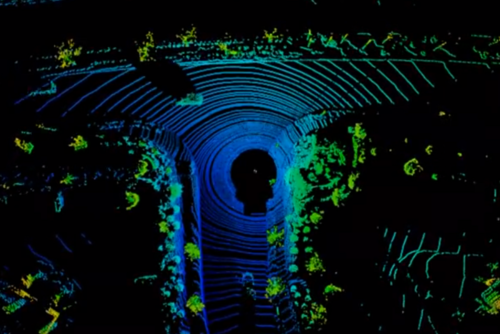
It may be useful to note that not all raw point clouds coming from sensors are completely unordered. For example, the points from a LiDAR scanner are ordered by the specific angles of the laser scans, which can be seen as rings in the point cloud (shown in the figure below). The discontinuities along each ring could be used to provide trackable feature information for SLAM algorithms, and would be harder to recover if the point cloud is represented in an unordered manner.
Code
Code for PointNet++ can be found at: https://github.com/charlesq34/pointnet2
Conclusion
In this work, we propose PointNet++, a powerful neural network architecture for processing point sets sampled in a metric space. PointNet++ recursively functions on a nested partitioning of the input point set, and is effective in learning hierarchical features with respect to the distance metric. To handle the non uniform point sampling issue, we propose two novel set abstraction layers that intelligently aggregate multi-scale information according to local point densities. These contributions enable us to achieve state-of-the-art performance on challenging benchmarks of 3D point clouds. In the future, it’s worthwhile thinking how to accelerate inference speed of our proposed network especially for MSG and MRG layers by sharing more computation in each local regions. It’s also interesting to find applications in higher dimensional metric spaces where CNN based method would be computationally unfeasible while our method can scale well.
Sources
- Charles R. Qi, Li Yi, Hao Su, Leonidas J. Guibas. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space, 2017
- Charles R. Qi, Hao Su, Kaichun Mo, Leonidas J. Guibas. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation, 2017
- Charles R. Qi, “charlesq34/pointnet2.” GitHub, 25 Feb. 2018, github.com/charlesq34/pointnet2.