Patch Based Convolutional Neural Network for Whole Slide Tissue Image Classification: Difference between revisions
| Line 15: | Line 15: | ||
$$P(X, H) = \prod_{i = 1}^N P(X_{i,1}, \dots , X_{i,N_i}| H_i)P(H_i) \quad \quad \quad \quad (1) $$ | $$P(X, H) = \prod_{i = 1}^N P(X_{i,1}, \dots , X_{i,N_i}| H_i)P(H_i) \quad \quad \quad \quad (1) $$ | ||
<math>Hi = {H_{i, 1}, \dots, H_{i, Ni}}</math> denotes the set of hidden variables for instances in the bag <math>X_i</math> and <math>H_{i, j}</math> indicates whether the patch <math>X_{i,j}</math> is discriminative for <math>y_i</math> (it is discriminative if estimated label of the instance coincides with the label of the whole bag). Authors assume that <math>X_{i, j}</math> is independent from hidden labels of all other instances in the i-th bag, therefore <math>(1)</math> can be simplified as: | <math>Hi = {H_{i, 1}, \dots, H_{i, Ni}}</math> denotes the set of hidden variables for instances in the bag <math>X_i</math> and <math>H_{i, j}</math> indicates whether the patch <math>X_{i,j}</math> is discriminative for <math>y_i</math> (it is discriminative if estimated label of the instance coincides with the label of the whole bag). Authors assume that <math>X_{i, j}</math> is independent from hidden labels of all other instances in the i-th bag, therefore <math>(1)</math> can be simplified as: | ||
$$P(X, H) = \prod_{i = 1}^{N} \prod_{j=1}^{N_i} P(X_{i, j}| H_{i, j})P(H_{i, j}) \quad \quad (2)$$ | |||
==References== | ==References== | ||
Revision as of 20:18, 15 November 2021
Presented by
Cassandra Wong, Anastasiia Livochka, Maryam Yalsavar, David Evans
Introduction
Despite the fact that CNN are well-known for their success in image classification, it is computationally impossible to use them for cancer classification. This problem is due to high-resolution images that cancer classification is dealing with. As a result, this paper argues that using a patch level CNN can outperform an image level based one and considers two main challenges in patch level classification – aggregation of patch-level classification results and existence of non-discriminative patches. For dealing with these challenges, training a decision fusion model and an Expectation-Maximization (EM) based method for locating the discriminative patches are suggested respectively. At the end the authors proved their claims and findings by testing their model to the classification of glioma and non-small-cell lung carcinoma cases.
Previous Work
EM-based method with CNN
The high-resolution image is modelled as a bag, and patches extracted from it are instances that form a specific bag. The ground truth labels are provided for the bag only, so we model the labels of an instance (discriminative or not) as a hidden binary variable. Hidden binary variables are estimated by the Expectation-Maximization algorithm. A summary of the proposed approach can be found in Fig.2:
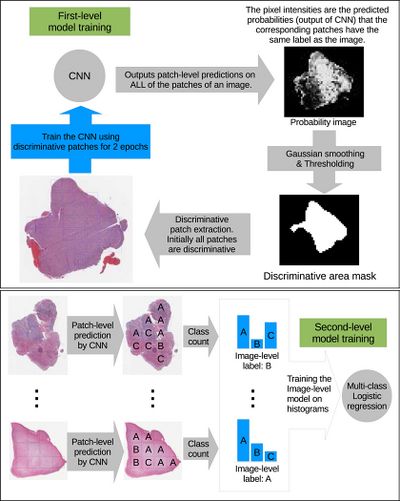
In this paper [math]\displaystyle{ X = \{X_1, \dots, X_N\} }[/math] denotes dataset containing [math]\displaystyle{ N }[/math] bags. A bag [math]\displaystyle{ X_i= \{X_{i,1}, X_{i,2}, \dots, X_{i, N_i}\} }[/math] consists of [math]\displaystyle{ N_i }[/math] pathes (instances) and [math]\displaystyle{ X_{i,j} = \lt x_{i,j}, y_j\gt }[/math] denotes j-th instance and it’s label in i-th bag. We assume bags are i.i.d. (independent identically distributed), [math]\displaystyle{ X }[/math] and associated hidden labels [math]\displaystyle{ H }[/math] are generated by the following model: $$P(X, H) = \prod_{i = 1}^N P(X_{i,1}, \dots , X_{i,N_i}| H_i)P(H_i) \quad \quad \quad \quad (1) $$ [math]\displaystyle{ Hi = {H_{i, 1}, \dots, H_{i, Ni}} }[/math] denotes the set of hidden variables for instances in the bag [math]\displaystyle{ X_i }[/math] and [math]\displaystyle{ H_{i, j} }[/math] indicates whether the patch [math]\displaystyle{ X_{i,j} }[/math] is discriminative for [math]\displaystyle{ y_i }[/math] (it is discriminative if estimated label of the instance coincides with the label of the whole bag). Authors assume that [math]\displaystyle{ X_{i, j} }[/math] is independent from hidden labels of all other instances in the i-th bag, therefore [math]\displaystyle{ (1) }[/math] can be simplified as: $$P(X, H) = \prod_{i = 1}^{N} \prod_{j=1}^{N_i} P(X_{i, j}| H_{i, j})P(H_{i, j}) \quad \quad (2)$$