Patch Based Convolutional Neural Network for Whole Slide Tissue Image Classification: Difference between revisions
| Line 9: | Line 9: | ||
==EM-based method with CNN== | ==EM-based method with CNN== | ||
The high-resolution image is modelled as a bag and patches extracted from it are instances that form a specific bag. The ground truth labels are provided for the bag only, so we model the labels of an instance (discriminative or not) as a hidden binary variable. Hidden binary variables are estimated by the Expectation-Maximization algorithm. A summary of the proposed approach can be found in Fig.2: | The high-resolution image is modelled as a bag, and patches extracted from it are instances that form a specific bag. The ground truth labels are provided for the bag only, so we model the labels of an instance (discriminative or not) as a hidden binary variable. Hidden binary variables are estimated by the Expectation-Maximization algorithm. A summary of the proposed approach can be found in Fig.2: | ||
[[File:fig2_model_architecture.jpeg|center|500px]] | [[File:fig2_model_architecture.jpeg|center|500px]] | ||
<div align="center">Figure 2: Top: A CNN is trained on patches and EM-based method iteratively eliminates non-discriminative patches. <br> Bottom: An image-level decision fusion model is trained on histograms of patch-level predictions to predict the image-level label | <div align="center">Figure 2: Top: A CNN is trained on patches and EM-based method iteratively eliminates non-discriminative patches. <br> Bottom: An image-level decision fusion model is trained on histograms of patch-level predictions to predict the image-level label | ||
</div> | </div> | ||
In this paper <math>X = \{X_1, X_n\}</math> denotes dataset containing Nbags. A bag | In this paper <math>X = \{X_1, \dots, X_n\}</math> denotes dataset containing Nbags. A bag <math>X_i= \{X_{i,1}, X_{i,2}, \dots, X_{i, N_i}\}</math> consists of <math>N_i</math> pathes (instances) and <math>X_{i,j} = <x_{i,j}, y_j></math> denotes j-th instance and it’s label in i-th bag. We assume bags are i.i.d. (independent identically distributed), <math>X</math> and associated hidden labels <math>H</math> are generated by the following model: | ||
==References== | ==References== | ||
Revision as of 19:56, 15 November 2021
Presented by
Cassandra Wong, Anastasiia Livochka, Maryam Yalsavar, David Evans
Introduction
Despite the fact that CNN are well-known for their success in image classification, it is computationally impossible to use them for cancer classification. This problem is due to high-resolution images that cancer classification is dealing with. As a result, this paper argues that using a patch level CNN can outperform an image level based one and considers two main challenges in patch level classification – aggregation of patch-level classification results and existence of non-discriminative patches. For dealing with these challenges, training a decision fusion model and an Expectation-Maximization (EM) based method for locating the discriminative patches are suggested respectively. At the end the authors proved their claims and findings by testing their model to the classification of glioma and non-small-cell lung carcinoma cases.
Previous Work
EM-based method with CNN
The high-resolution image is modelled as a bag, and patches extracted from it are instances that form a specific bag. The ground truth labels are provided for the bag only, so we model the labels of an instance (discriminative or not) as a hidden binary variable. Hidden binary variables are estimated by the Expectation-Maximization algorithm. A summary of the proposed approach can be found in Fig.2:
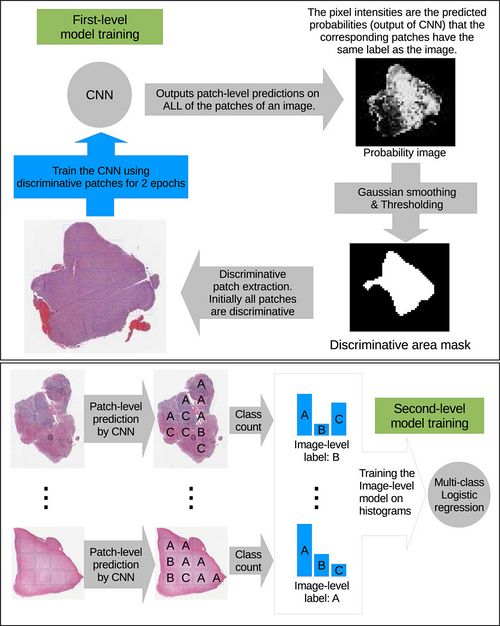
Bottom: An image-level decision fusion model is trained on histograms of patch-level predictions to predict the image-level label
In this paper [math]\displaystyle{ X = \{X_1, \dots, X_n\} }[/math] denotes dataset containing Nbags. A bag [math]\displaystyle{ X_i= \{X_{i,1}, X_{i,2}, \dots, X_{i, N_i}\} }[/math] consists of [math]\displaystyle{ N_i }[/math] pathes (instances) and [math]\displaystyle{ X_{i,j} = \lt x_{i,j}, y_j\gt }[/math] denotes j-th instance and it’s label in i-th bag. We assume bags are i.i.d. (independent identically distributed), [math]\displaystyle{ X }[/math] and associated hidden labels [math]\displaystyle{ H }[/math] are generated by the following model: