One pixel attack for fooling deep neural networks: Difference between revisions
No edit summary |
|||
| Line 14: | Line 14: | ||
= Methodology = | = Methodology = | ||
We | == Problem Description == | ||
Let | |||
We can formalize the generation of adversarial images as an constrained optimization problem. We are given a classifier '''F''' and targeted adversarial class '''adv'''. Let '''x''' be the vectorized form of an image. Let F_adv('''x''') represent the probability assigned to the targeted class '''adv''' for vector '''x''' by the given classifier. Let e('''x''') represent an additive adversarial perturbation vector for image '''x'''. The goal of the targeted attack adversary is to find the perturbation vector with constrained size(norm) that maximizes the probability assigned to the targeted class by the classifier. Formally | |||
[[File:ONE_PIXEL_CSP1.png | center ]] | |||
For few-pixel attack, the problem statement is changed slightly. We constrain on the number of non-zero elements of the perturbation vector instead of the norm of the vector. | |||
[[File:ONE_PIXEL_CSP2.png | center ]] | |||
For the usual adversarial case, we can shift '''x''' in all dimensions, but the strength(norm) of the shift is bounded by L. For our one-pixel attack case, we are using the second equation with d=1. '''x''' is only allowed to be perturbed along a single axis, so the degree of freedom of the shift is greatly reduces. However, the shift in the one axis can be of arbitrary strength. | |||
== Differential Evolution == | |||
Differential evolution(DE) is a population based optimization algorithm belonging to the class of evolutionary algorithms(EA). For DE, in the selection process, the population is in a way "segmented" into families( offspring and parents ), and the most optimal from each family is chosen. This segmentation allows DE to keep more diversity in each iteration than other EAs and makes it more suitable for complex multi-modal optimization problems. Additionally, DE does not use gradient information, which makes it suitable for our problem. | |||
= Evaluation and Results = | = Evaluation and Results = | ||
Revision as of 23:02, 25 March 2018
Presented by
1. Ziheng Chu
2. Minghao Lu
3. Qi Mai
4. Qici Tan
Introduction
Methodology
Problem Description
We can formalize the generation of adversarial images as an constrained optimization problem. We are given a classifier F and targeted adversarial class adv. Let x be the vectorized form of an image. Let F_adv(x) represent the probability assigned to the targeted class adv for vector x by the given classifier. Let e(x) represent an additive adversarial perturbation vector for image x. The goal of the targeted attack adversary is to find the perturbation vector with constrained size(norm) that maximizes the probability assigned to the targeted class by the classifier. Formally
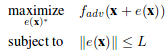
For few-pixel attack, the problem statement is changed slightly. We constrain on the number of non-zero elements of the perturbation vector instead of the norm of the vector.

For the usual adversarial case, we can shift x in all dimensions, but the strength(norm) of the shift is bounded by L. For our one-pixel attack case, we are using the second equation with d=1. x is only allowed to be perturbed along a single axis, so the degree of freedom of the shift is greatly reduces. However, the shift in the one axis can be of arbitrary strength.
Differential Evolution
Differential evolution(DE) is a population based optimization algorithm belonging to the class of evolutionary algorithms(EA). For DE, in the selection process, the population is in a way "segmented" into families( offspring and parents ), and the most optimal from each family is chosen. This segmentation allows DE to keep more diversity in each iteration than other EAs and makes it more suitable for complex multi-modal optimization problems. Additionally, DE does not use gradient information, which makes it suitable for our problem.