One-Shot Object Detection with Co-Attention and Co-Excitation: Difference between revisions
No edit summary |
No edit summary |
||
| Line 60: | Line 60: | ||
\end{align} | \end{align} | ||
where ''x'' is a vector on which this operation is applied, ''z'' is a vector which is taken as an input reference, ''i'' is the index of output position, ''j'' is the index that enumerates over all possible positions, ''C(z)'' is a normalization factor which is a function of ''z'' and ''y'' is the output of this operation. | where ''x'' is a vector on which this operation is applied, ''z'' is a vector which is taken as an input reference, ''i'' is the index of output position, ''j'' is the index that enumerates over all possible positions, ''C(z)'' is a normalization factor which is a function of ''z'', <math>f(x_i, z_j)</math> is a pairwise function like Gaussian, Embedded Gaussian, Dot product, concatenation, etc., <math>g(z_j)</math> is a linear function of the form <math>W_z \times z_j</math>, and ''y'' is the output of this operation. | ||
Let the feature maps obtained from the ResNet-50 model be <math> \phi{(I)} \in R^{N \times W_I \times H_I} </math> for target image ''I'' and <math> \phi{(p)} \in R^{N \times W_p \times H_p} </math> for query image ''p''. | Let the feature maps obtained from the ResNet-50 model be <math> \phi{(I)} \in R^{N \times W_I \times H_I} </math> for target image ''I'' and <math> \phi{(p)} \in R^{N \times W_p \times H_p} </math> for query image ''p''. | ||
| Line 132: | Line 132: | ||
where <math>L_{CE}</math> is the cross-entropy loss, <math>L_{Reg}</math> is the regression loss for bounding boxes of Faster R-CNN and <math>L_{MR}</math> is the margin-based ranking loss defined above. | where <math>L_{CE}</math> is the cross-entropy loss, <math>L_{Reg}</math> is the regression loss for bounding boxes of Faster R-CNN and <math>L_{MR}</math> is the margin-based ranking loss defined above. | ||
For this paper, <math>m^+</math> = 0.7, <math>m^-</math> = 0.3, <math>\lambda</math> = 3, K = 128, <math>f(x_i, z_j)</math> in eq. (1) is a dot product operation, | For this paper, <math>m^+</math> = 0.7, <math>m^-</math> = 0.3, <math>\lambda</math> = 3, K = 128, C(z) in eq. (1) is the total number of elements in a single feature map of vector ''z'', and <math>f(x_i, z_j)</math> in eq. (1) is a dot product operation. | ||
\begin{align} | |||
f(x_i, z_j) = \alpha(x_i)^T \beta(z_j) \tag{12} \label{eq:op11} | |||
\end{align} | |||
\begin{align} | |||
\alpha(x_i) = W_{\alpha}^T x_i \tag{13} \label{eq:op12} | |||
\end{align} | |||
\begin{align} | |||
\beta(z_j) = W_{\beta}^T z_j \tag{14} \label{eq:op13} | |||
\end{align} | |||
Revision as of 18:03, 21 November 2020
Presented By
Gautam Bathla
Background
Object Detection is a technique where the model gets an image as an input and outputs the class and location of all the objects present in the image.
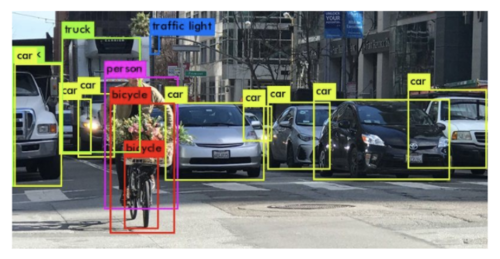
Figure 1 shows an example where the model identifies and locates all the instances of different objects present in the image successfully. It encloses each object within a bounding box and annotates each box with the class of the object present inside the box.
State-of-the-art object detectors are trained on thousands of images for different classes before the model can accurately predict the class and spatial location for unseen images belonging to the classes the model has been trained on. When a model is trained with K labeled instances for each of N classes, then this setting is known as N-way K-shot classification. K = 0 for zero-shot learning, K = 1 for one-shot learning and k > 1 for few-shot learning.
Introduction
The problem this paper is trying to tackle is given a query image p, the model needs to find all the instances in the target image of the object present in the query image. Consider the same task when given to a human, i.e. the task of identifying and locating the instances of a never-before-seen object in the target image based on the query image, the person will try to compare different characteristics of the object like shape, texture, color, etc. along with applying attention for localization. The human visual system can achieve this even in varying conditions like lighting conditions, viewing angles, etc. The authors are trying to incorporate the same functionality into the model to achieve this task. The target and query image do not need to be exactly the same and are allowed to have variations as long as they share some attributes so that they can belong to the same category.
In this paper, the authors have made contributions to three technical areas. First is the use of non-local operations to generate better region proposals for the target image based on the query image. This operation can be thought of as a co-attention mechanism. The second contribution is proposing a Squeeze and Co-Excitation mechanism to identify and give more importance to relevant features to filter out relevant proposals and hence the instances in the target image. Third, the authors designed a margin-based ranking loss which will be useful for predicting the similarity of region proposals with the given query image irrespective of whether the label of the class is seen or unseen during the training process.
Previous Work
All state-of-the-art object detectors are variants of deep convolutional neural networks. There are two types of object detectors:
1) Two-Stage Object Detectors: These types of detectors generate region proposals in the first stage whereas classifying and refining the proposals in the second stage. Eg. FasterRCNN[1].
2) One Stage Object Detectors: These types of detectors directly predict bounding boxes and their corresponding labels based on a fixed set of anchors. Eg. CornerNet[2].
There are some of the approaches that have been proposed to tackle the problem of few-shot object detection. These approaches are based on transfer learning[3], meta-learning[4], and metric-learning[5].
1) Transfer Learning: Chen et al.[3] proposed a regularization technique to reduce overfitting when the model is trained on just a few instances for each class belonging to unseen classes.
2) Meta-Learning: Kang et al.[4] trained a meta-model to re-weight the learned weights of an image extracted from the base model.
3) Metric-Learning: These frameworks replace the conventional classifier layer with the metric-based classifier layer.
Approach
Let's define some notations before diving into the approach of this paper. Let 'C' be the set of classes for this object detection task. Since one-shot object detection task needs unseen classes during inference time, therefore we divide the set of classes into two categories as follows:
where [math]\displaystyle{ C_0 }[/math] represents the classes that the model is trained on and [math]\displaystyle{ C_1 }[/math] represents the classes on which the inference is done.
The redefined problem statement. Given a query image belonging to a class in set [math]\displaystyle{ C_1 }[/math], the task is to predict all the instances of that object in the target image. The architecture of this model is based on FasterRCNN[1] and ResNet-50[6] has been used as the backbone for extracting features from the images. To tackle this problem, the authors have proposed the following techniques: Non-Local object proposals, Squeeze and Co-excitation mechanism, and margin-based ranking loss.
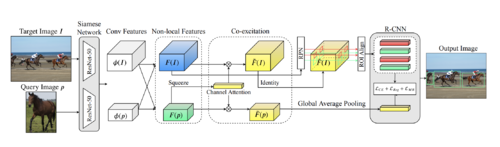
Figure 2 shows the architecture of the model proposed in this paper. The target image and the query image are first passed through the ResNet-50 module to extract the features from the same convolutional layer. The features obtainer are next passed into Non-local block as input and the output consists of a new set of features for each of the images. The new feature set of the target image is then passed to RPN module to generate proposals. Then new features are inputted into Squeeze and Co-excitation block which outputs the re-weighted features which are then passed into the RCNN module. RCNN module also consists of a new loss that is designed by the authors which helps to rank proposals in order of their relevance. Next, we will look at each of the three proposals used in the paper in detail.
Non-Local Object Proposals
The need for non-local object proposals arises because the RPN module used in Faster R-CNN[1] has access to bounding box information for each class in the training dataset. The dataset used for training and inference in the case of Faster R-CNN[1] is not exclusive which is not the case here. In this problem, as we have defined above that we divide the dataset into two parts, one part is used for training and the other is used during inference. Therefore, the classes in the two sets are exclusive. If the conventional RPN module is used, then the module will not be able to generate good proposals for images during inference because it will not have any information about the presence of bounding-box for those classes.
To resolve this problem, a non-local operation is applied to both sets of features. This non-local operation is defined as: \begin{align} y_i = \frac{1}{C(z)} \sum_{\forall j}^{} f(x_i, z_j)g(z_j) \tag{1} \label{eq:op} \end{align}
where x is a vector on which this operation is applied, z is a vector which is taken as an input reference, i is the index of output position, j is the index that enumerates over all possible positions, C(z) is a normalization factor which is a function of z, [math]\displaystyle{ f(x_i, z_j) }[/math] is a pairwise function like Gaussian, Embedded Gaussian, Dot product, concatenation, etc., [math]\displaystyle{ g(z_j) }[/math] is a linear function of the form [math]\displaystyle{ W_z \times z_j }[/math], and y is the output of this operation.
Let the feature maps obtained from the ResNet-50 model be [math]\displaystyle{ \phi{(I)} \in R^{N \times W_I \times H_I} }[/math] for target image I and [math]\displaystyle{ \phi{(p)} \in R^{N \times W_p \times H_p} }[/math] for query image p.
We can express the extended feature maps as:
\begin{align} F(I) = \phi{(I)} \oplus \psi{(I;p)} \in R^{N \times W_I \times H_I} \tag{2} \label{eq:o1} \end{align} \begin{align} F(p) = \phi{(p)} \oplus \psi{(p;I)} \in R^{N \times W_p \times H_p} \tag{3} \label{eq:op2} \end{align}
where F(I) denotes the extended feature map for target image I, F(p) denotes the extended feature map for query image p and [math]\displaystyle{ \oplus }[/math] denotes element-wise sum over the feature maps [math]\displaystyle{ \phi{} }[/math] and [math]\displaystyle{ \psi{} }[/math]
As can be seen above, the extended feature set for the target image I does not only contain features from I but also the weighted sum of the target image and the query image. The same can be observed for the query image. This weighted sum is basically a co-attention mechanism and with the help of extended feature maps, better proposals are generated when inputted to the RPN module.
Squeeze and Co-Excitation
The two feature maps generated from the non-local block above can be further related by identifying the important channels and therefore, re-weighting the weights of the channels. This is the basic purpose of this module. The Squeeze layer summarizes each feature map by applying Global Average Pooling (GAP) on the extended feature map for the query image. The Co-Excitation layer gives attention to feature channels that are important for evaluating the similarity metric. The whole block can be represented as:
\begin{align} SCE(F(I), F(P)) = w \tag{4} \label{eq:op3} \end{align} \begin{align} F(\tilde{P}) = w \odot F(P) \tag{5} \label{eq:op4} \end{align} \begin{align} F(\tilde{I}) = w \odot F(I) \tag{6} \label{eq:op5} \end{align}
where w is the excitation vector, [math]\displaystyle{ F(\tilde{P}) }[/math] and [math]\displaystyle{ F(\tilde{I}) }[/math] are the re-weighted features maps for query and target image respectively.
In between the Squeeze layer and Co-Excitation layer, there exist two fully-connected layers followed by a sigmoid layer which helps to learn the excitation vector w. The Channel Attention module in the architecture is basically these fully-connected layers followed by a sigmoid layer.
Margin-based Ranking Loss
Suppose that there are K candidate proposals are chosen among the proposals generated by the RPN module on the target image, there is a need to rank these proposals such that the most relevant proposals are at the top of the list. For this, the authors have designed a two-layer MLP network ending with a two-way softmax layer. In the first stage of training, each of the K proposals is annotated with 0 or 1 based on the IoU value of the proposal with the ground-truth bounding box. If the IoU value is greater than 0.5 then that proposal is labeled as 1 (foreground) and 0 (background) otherwise.
Let q be the feature vector obtained after applying GAP to the query image patch obtained from the Squeeze and Co-Excitation block and r be the feature vector obtained after applying GAP to the region proposals generated by the RPN module. The two vectors are concatenated to form a new vector x which is the input to the two-layer MLP network designed.
\begin{align} x = [r^T;q^T] \tag{7} \label{eq:op6} \end{align}
Let M be the model representing the two-layer MLP network, then \begin{align} s = M(x) \tag{8} \label{eq:op7} \end{align}
where s is the probability of being a foreground proposal based on the query image patch q. The margin-based ranking loss is given by:
\begin{align} L_{MR}(\{x_i\}) = \sum_{i=1}^{K}y_i \times max\{m^+ - s_i, 0\} + (1-y_i) \times max\{s_i - m^-, 0\} + \delta_{i} \tag{9} \label{eq:op8} \end{align} \begin{align} \delta_{i} = \sum_{j=i+1}^{K}[y_i = y_j] \times max\{|s_i - s_j| - m^-, 0\} + [y_i \ne y_j] \times max\{m^+ - |s_i - s_j|, 0\} \tag{10} \label{eq:op9} \end{align}
where [.] is the Iversion bracket, i.e. the output will be 1 if the condition inside the bracket is true and 0 otherwise, [math]\displaystyle{ m^+ }[/math] is the expected upper bound probability for predicting a foreground proposal, [math]\displaystyle{ m^- }[/math] is the expected lower bound probability for predicting a background proposal.
The total loss for the model is given as:
\begin{align} L = L_{CE} + L_{Reg} + \lambda \times L_{MR} \tag{11} \label{eq:op10} \end{align}
where [math]\displaystyle{ L_{CE} }[/math] is the cross-entropy loss, [math]\displaystyle{ L_{Reg} }[/math] is the regression loss for bounding boxes of Faster R-CNN and [math]\displaystyle{ L_{MR} }[/math] is the margin-based ranking loss defined above.
For this paper, [math]\displaystyle{ m^+ }[/math] = 0.7, [math]\displaystyle{ m^- }[/math] = 0.3, [math]\displaystyle{ \lambda }[/math] = 3, K = 128, C(z) in eq. (1) is the total number of elements in a single feature map of vector z, and [math]\displaystyle{ f(x_i, z_j) }[/math] in eq. (1) is a dot product operation. \begin{align} f(x_i, z_j) = \alpha(x_i)^T \beta(z_j) \tag{12} \label{eq:op11} \end{align} \begin{align} \alpha(x_i) = W_{\alpha}^T x_i \tag{13} \label{eq:op12} \end{align} \begin{align} \beta(z_j) = W_{\beta}^T z_j \tag{14} \label{eq:op13} \end{align}