On The Convergence Of ADAM And Beyond: Difference between revisions
| Line 69: | Line 69: | ||
'''Theorem 3.''' For any constant <math>\beta_1,\beta_2 \in [0,1)</math> such that <math>\beta_2 < \sqrt{\beta_2}</math>, there is a stochastic convex optimization problem for which ADAM does not converge to the optimal solution. | '''Theorem 3.''' For any constant <math>\beta_1,\beta_2 \in [0,1)</math> such that <math>\beta_2 < \sqrt{\beta_2}</math>, there is a stochastic convex optimization problem for which ADAM does not converge to the optimal solution. | ||
Kingama & Ba (2015) mentioned that the analysis of ADAM relies on decreasing <math> \beta_1 </math> over time. As <math> \beta_2 </math> is the critical parameter, the examples could be easily extended to the case where <math> \beta_1 </math> is decreasing over time. The paper only focus on proving non-convergence of ADAM when <math> \beta_1 </math> is constant. | |||
= AMSGrad as an improvement to ADAM = | = AMSGrad as an improvement to ADAM = | ||
Revision as of 17:19, 5 April 2018
Introduction
Stochastic gradient descent (SGD) is currently the dominant method of training deep networks. Variants of SGD that scale the gradients using information from past gradients have been very successful, since the learning rate is adjusted on a per-feature basis, with ADAGRAD being one example. However, ADAGRAD performance deteriorates when loss functions are nonconvex and gradients are dense. Several variants of ADAGRAD, such as RMSProp, ADAM, ADADELTA, and NADAM have been proposed, which address the issue by using exponential moving averages of squared past gradients, thereby limiting the update to only rely on the past few gradients. The following formula shows the per-parameter update for which is then vectorized: [math]\displaystyle{ g_{t, i} = \nabla_\theta J( \theta_{t, i} ). }[/math]
After vectorizing the update per-parameter using SGD becomes: [math]\displaystyle{ \theta_{t+1, i} = \theta_{t, i} - \eta \cdot g_{t, i}. }[/math]
The update for the parameter in the next step is calculated using the matrix vector product: [math]\displaystyle{ \theta_{t+1} = \theta_{t} - \dfrac{\eta}{\sqrt{G_{t} + \epsilon}} \odot g_{t}. }[/math]
This paper focuses strictly on the pitfalls in convergence of the ADAM optimizer from a theoretical standpoint and proposes a novel improvement to ADAM called AMSGrad. The paper introduces the idea that it is possible for ADAM to get "stuck" in its weighted average history, preventing it from converging to an optimal solution. For example, in an experiment there may be a large spike in the gradient during some mini-batches. But since ADAM weighs the current update by the exponential moving averages of squared past gradients, the effect of the large spike in gradient is lost. To tackle these issues, several variants of ADAGRAD hav been proposed. The authors' analysis suggest that this can be prevented through novel but simple adjustments to the ADAM optimization algorithm, which can improve convergence. This paper is published in ICLR 2018.
Notation
The paper presents the following framework as a generalization to all training algorithms, allowing us to fully define any specific variant such as AMSGrad or SGD entirely within it:

Where we have [math]\displaystyle{ x_t }[/math] as our network parameters defined within a vector space [math]\displaystyle{ \mathcal{F} }[/math]. [math]\displaystyle{ \prod_{\mathcal{F}} (y) = }[/math] the projection of [math]\displaystyle{ y }[/math] on to the set [math]\displaystyle{ \mathcal{F} }[/math]. [math]\displaystyle{ \psi_t }[/math] and [math]\displaystyle{ \phi_t }[/math] correspond to arbitrary functions we will provide later, The former maps from the history of gradients to [math]\displaystyle{ \mathbb{R}^d }[/math] and the latter maps from the history of the gradients to positive semi definite matrices. And finally [math]\displaystyle{ f_t }[/math] is our loss function at some time [math]\displaystyle{ t }[/math], the rest should be pretty self explanatory. Using this framework and defining different [math]\displaystyle{ \psi_t }[/math] , [math]\displaystyle{ \phi_t }[/math] will allow us to recover all different kinds of training algorithms under this one roof.
SGD As An Example
To recover SGD using this framework we simply select [math]\displaystyle{ \phi_t (g_1, \dotsc, g_t) = g_t }[/math], [math]\displaystyle{ \psi_t (g_1, \dotsc, g_t) = I }[/math] and [math]\displaystyle{ \alpha_t = \alpha / \sqrt{t} }[/math]. It is easy to see that no transformations are ultimately applied to any of the parameters based on any gradient history other than the most recent from [math]\displaystyle{ \phi_t }[/math] and that [math]\displaystyle{ \psi_t }[/math] in no way transforms any of the parameters by any specific amount as [math]\displaystyle{ V_t = I }[/math] has no impact later on.
ADAGRAD As Another Example
To recover ADAGRAD, we select [math]\displaystyle{ \phi_t (g_1, \dotsc, g_t) = g_t }[/math], [math]\displaystyle{ \psi_t (g_1, \dotsc, g_t) = \frac{\sum_{i=1}^{t} g_i^2}{t} }[/math], and [math]\displaystyle{ \alpha_t = \alpha / \sqrt{t} }[/math]. Therefore, compared to SGD, ADAGRAD uses a different step size for each parameter, based on the past gradients for that parameter; the learning rate becomes [math]\displaystyle{ \alpha_t = \alpha / \sqrt{\sum_i g_{i,j}^2} }[/math] for each parameter [math]\displaystyle{ j }[/math]. The authors note that this scheme is quite efficient when the gradients are sparse.
ADAM As Another Example
Once you can convince yourself that the recovery of SGD from the generalized framework is correct, you should understand the framework enough to see why the following setup for ADAM will allow us to recover the behaviour we want. ADAM has the ability to define a "learning rate" for every parameter based on how much that parameter moves over time (a.k.a its momentum) supposedly to help with the learning process.
In order to do this, we will choose [math]\displaystyle{ \phi_t (g_1, \dotsc, g_t) = (1 - \beta_1) \sum_{i=0}^{t} {\beta_1}^{t - i} g_t }[/math], psi to be [math]\displaystyle{ \psi_t (g_1, \dotsc, g_t) = (1 - \beta_2) }[/math]diag[math]\displaystyle{ ( \sum_{i=0}^{t} {\beta_2}^{t - i} {g_t}^2) }[/math], and keep [math]\displaystyle{ \alpha_t = \alpha / \sqrt{t} }[/math]. This setup is equivalent to choosing a learning rate decay of [math]\displaystyle{ \alpha / \sqrt{\sum_i g_{i,j}} }[/math] for [math]\displaystyle{ j \in [d] }[/math].
From this, we can now see that [math]\displaystyle{ m_t }[/math] gets filled up with the exponentially weighted average of the history of our gradients that we have come across so far in the algorithm. And that as we proceed to update we scale each one of our parameters by dividing out [math]\displaystyle{ V_t }[/math] (in the case of diagonal it is just one over the diagonal entry) which contains the exponentially weighted average of each parameter's momentum ([math]\displaystyle{ {g_t}^2 }[/math]) across our training so far in the algorithm. Thus each parameter has its own unique scaling by its second moment or momentum. Intuitively, from a physical perspective, if each parameter is a ball rolling around in the optimization landscape what we are now doing is instead of having the ball change positions on the landscape at a fixed velocity (i.e. momentum of 0) the ball now has the ability to accelerate and speed up or slow down if it is on a steep hill or flat trough in the landscape (i.e. a momentum that can change with time).
[math]\displaystyle{ \Gamma_t }[/math], an Interesting Quantity
Now that we have an idea of what ADAM looks like in this framework, let us now investigate the following:
Which essentially measure the change of the "Inverse of the learning rate" across time (since we are using alpha's as step sizes). A key observation is that for SGD and ADAGRAD, [math]\displaystyle{ \Gamma_t \succeq 0 }[/math] for all [math]\displaystyle{ t \in [T] }[/math], which simply follows from the update rules of SGD and ADAGRAD. Looking back to our example of SGD it's not hard to see that this quantity is strictly positive semidefinite, which leads to "non-increasing" learning rates, which is a desired property. However, that is not the case with ADAM, and can pose a problem in a theoretical and applied setting. The problem ADAM can face is that [math]\displaystyle{ \Gamma_t }[/math] can potentially be indefinite for [math]\displaystyle{ t \in [T] }[/math], which the original proof assumed it could not be. The math for this proof is VERY long so instead we will opt for an example to showcase why this could be an issue.
Consider the loss function [math]\displaystyle{ f_t(x) = \begin{cases} Cx & \text{for } t \text{ mod 3} = 1 \\ -x & \text{otherwise} \end{cases} }[/math]
Where we have [math]\displaystyle{ C \gt 2 }[/math] and [math]\displaystyle{ \mathcal{F} }[/math] is [math]\displaystyle{ [-1,1] }[/math]. Additionally we choose [math]\displaystyle{ \beta_1 = 0 }[/math] and [math]\displaystyle{ \beta_2 = 1/(1+C^2) }[/math]. We then proceed to plug this into our framework from before. This function is periodic and it's easy to see that it has the gradient of C once and then a gradient of -1 twice every period. It has an optimal solution of [math]\displaystyle{ x = -1 }[/math] (from a regret standpoint), but using ADAM we would eventually converge at [math]\displaystyle{ x = 1 }[/math], since [math]\displaystyle{ \psi_t }[/math] would scale down the [math]\displaystyle{ C }[/math] by a factor of almost [math]\displaystyle{ C }[/math] so that it's unable to "overpower" the multiple -1's.
We formalize this intuition in the results below.
Theorem 1. There is an online convex optimization problem where ADAM has non-zero average regret. i.e. [math]\displaystyle{ R_T/T\nrightarrow 0 }[/math] as [math]\displaystyle{ T\rightarrow \infty }[/math].
One might think that adding a small constant in the denominator of the update function can help avoid this issue by modifying the update for ADAM as follow: \begin{align} \hat x_{t+1} = x_t - \alpha_t m_t/\sqrt{V_t + \epsilon \mathbb{I}} \end{align}
The selection of [math]\displaystyle{ \epsilon }[/math] appears to be crucial for the performance of the algorithm in practice. However, this work shows that for any constant [math]\displaystyle{ \epsilon \gt 0 }[/math], there exists an online optimization setting where ADAM has non-zero average regret asymptotically.
Theorem 2. For any constant [math]\displaystyle{ \beta_1,\beta_2 \in [0,1) }[/math] such that [math]\displaystyle{ \beta_2 \lt \sqrt{\beta_2} }[/math], there is an online convex optimization problem where ADAM has non-zero average regret i.e. [math]\displaystyle{ R_T/T\nrightarrow 0 }[/math] as [math]\displaystyle{ T\rightarrow \infty }[/math].
The theorem shows that the convergence of the algorithm to the optimal solution will not be improved by momentum or regularization via [math]\displaystyle{ \varepsilon }[/math] with constant [math]\displaystyle{ \beta_1 }[/math] and [math]\displaystyle{ \beta_2 }[/math].
Theorem 3. For any constant [math]\displaystyle{ \beta_1,\beta_2 \in [0,1) }[/math] such that [math]\displaystyle{ \beta_2 \lt \sqrt{\beta_2} }[/math], there is a stochastic convex optimization problem for which ADAM does not converge to the optimal solution.
Kingama & Ba (2015) mentioned that the analysis of ADAM relies on decreasing [math]\displaystyle{ \beta_1 }[/math] over time. As [math]\displaystyle{ \beta_2 }[/math] is the critical parameter, the examples could be easily extended to the case where [math]\displaystyle{ \beta_1 }[/math] is decreasing over time. The paper only focus on proving non-convergence of ADAM when [math]\displaystyle{ \beta_1 }[/math] is constant.
AMSGrad as an improvement to ADAM
There is a very simple intuitive fix to ADAM to handle this problem. We simply scale our historical weighted average by the maximum we have seen so far to avoid the negative sign problem. There is a very simple one-liner adaptation of ADAM to get to AMSGRAD:

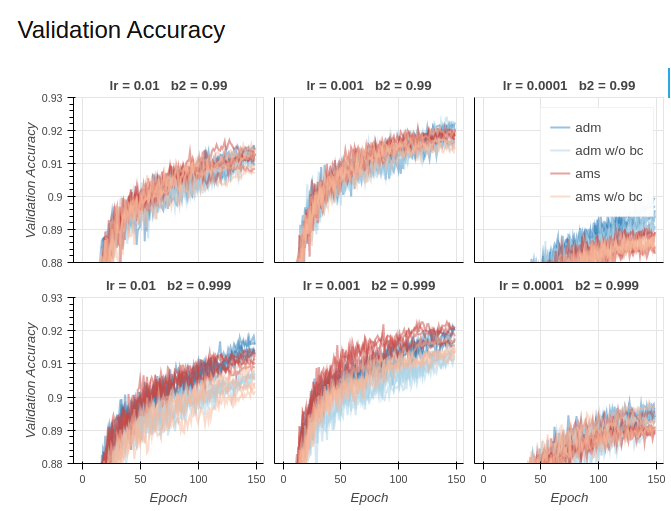
Below are some simple plots comparing ADAM and AMSGrad, the first are from the paper and the second are from another individual who attempted to recreate the experiments. The two plots somewhat disagree with one another so take this heuristic improvement with a grain of salt.
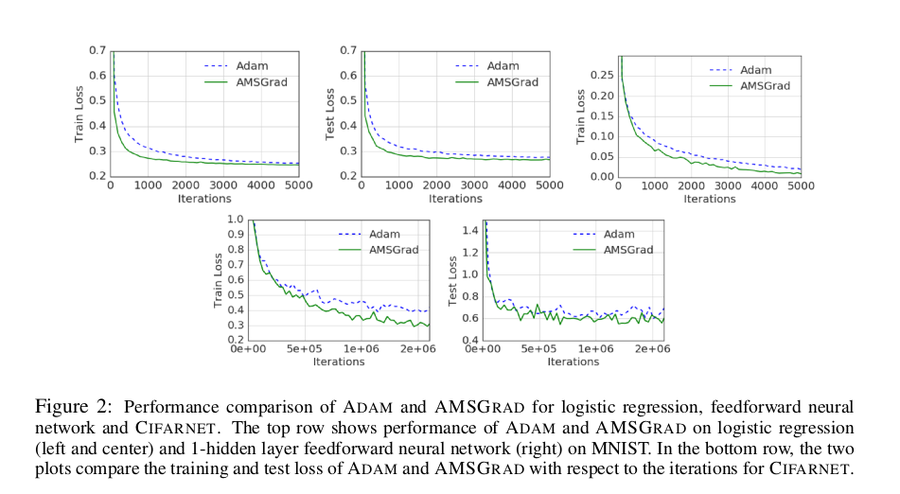
Here is another example of a one-dimensional convex optimization problem where ADAM fails to converge

Conclusion
The authors have introduced a framework for which they could view several different training algorithms. From there they used it to recover SGD as well as ADAM. In their recovery of ADAM the authors investigated the change of the inverse of the learning rate over time to discover in certain cases there were convergence issues. They proposed a new heuristic AMSGrad to help deal with this problem and presented some empirical results that show it may have helped ADAM slightly. Thanks for your time.
Critique
The contrived example which serves as the intuition to illustrate the failure of ADAM is not convincing, since we can construct similar failure examples for SGD as well. Consider the loss function
[math]\displaystyle{ f_t(x) = \begin{cases} -x & \text{for } t \text{ mod 2} = 1 \\ -\frac{1}{2} x^2 & \text{otherwise} \end{cases} }[/math]
where [math]\displaystyle{ x \in \mathcal{F} = [-a, 1], a \in [1, \sqrt{2}) }[/math]. The optimal solution is [math]\displaystyle{ x=1 }[/math], but starting from initial point [math]\displaystyle{ x_{t=0} \le -1 }[/math], SGD will converge to [math]\displaystyle{ x = -a }[/math]
Implementation
Keras implementation of AMSGrad : https://gist.github.com/kashif/3eddc3c90e23d84975451f43f6e917da
Source
1. Sashank J. Reddi and Satyen Kale and Sanjiv Kumar. "On the Convergence of Adam and Beyond." International Conference on Learning Representations. 2018