Obfuscated Gradients Give a False Sense of Security Circumventing Defenses to Adversarial Examples: Difference between revisions
No edit summary |
(Added Future Work.) |
||
| Line 7: | Line 7: | ||
= Methodology = | = Methodology = | ||
The paper assumes a lot of familiarity with adversarial attack literature. | The paper assumes a lot of familiarity with adversarial attack literature. The section below briefly explains some key concepts. | ||
== Background == | == Background == | ||
| Line 156: | Line 156: | ||
= Conclusion = | = Conclusion = | ||
In this paper, it was found that gradient masking is a common technique used by many defense proposal that claim to be robust against a very difficult class of adversarial attacks; white-box, iterative attacks. However, the authors found that they can be easily circumvented. Three attack methods are presented that were able to defeat 7 out of the 8 defense proposal accepted in the 2018 ICLR conference for these types of attacks. | In this paper, it was found that gradient masking is a common technique used by many defense proposal that claim to be robust against a very difficult class of adversarial attacks; white-box, iterative attacks. However, the authors found that they can be easily circumvented. Three attack methods are presented that were able to defeat 7 out of the 8 defense proposal accepted in the 2018 ICLR conference for these types of attacks. | ||
Some future work that can come out of this paper includes avoiding relying on obfuscated gradients for perceived robustness and use the evaluation approach to detect when the attach occurs. Early categorization of attacks using some supervised techniques can also help in critical evaluation of incoming data. | |||
= Critique = | = Critique = | ||
Revision as of 09:02, 18 November 2018
Introduction
Over the past few years, neural network models have been the source of major breakthroughs in a variety of computer vision problems. However, these networks have been shown to be susceptible to adversarial attacks. In these attacks, small humanly-imperceptible changes are made to images (that are correctly classified) which causes these models to misclassify with high confidence. These attacks pose a major threat that needs to be addressed before these systems can be deployed on a large scale, especially in safety-critical scenarios.
The seriousness of this threat has generated major interest in both the design and defense against them. In this paper, the authors identify a common technique employed by several recently proposed defenses and design a set of attacks that can be used to overcome them. The use of this technique, masking gradients, is so prevalent, that 7 out of the 8 defenses proposed in the ICLR 2018 conference employed them. The authors were able to circumvent the proposed defenses and successfully brought down the accuracy of their models to below 10%. Their reimplementation of each of the defenses and implementations of the attacks are available here.
Methodology
The paper assumes a lot of familiarity with adversarial attack literature. The section below briefly explains some key concepts.
Background
Adversarial Images Mathematically
Given an image [math]\displaystyle{ x }[/math] and a classifier [math]\displaystyle{ f(x) }[/math], an adversarial image [math]\displaystyle{ x' }[/math] satisfies two properties:
- [math]\displaystyle{ D(x,x') \lt \epsilon }[/math]
- [math]\displaystyle{ c(x') \neq c^*(x) }[/math]
Where [math]\displaystyle{ D }[/math] is some distance metric, [math]\displaystyle{ \epsilon }[/math] is a small constant, [math]\displaystyle{ c(x') }[/math] is the output class predicted by the model, and [math]\displaystyle{ c^*(x) }[/math] is the true class for input x. In words, the adversarial image is a small distance from the original image, but the classifier classifies it incorrectly.
Adversarial Attacks Terminology
- Adversarial attacks can be either black or white-box. In black box attacks, the attacker has access to the network output only, while white-box attackers have full access to the network, including its gradients, architecture and weights. This makes white-box attackers much more powerful. Given access to gradients, white-box attacks use back propagation to modify inputs (as opposed to the weights) with respect to the loss function.
- In untargeted attacks, the objective is to maximize the loss of the true class, [math]\displaystyle{ x'=x \mathbf{+} \lambda(sign(\nabla_xL(x,c^*(x)))) }[/math]. While in targeted attacks, the objective is to minimize loss for a target class [math]\displaystyle{ c^t(x) }[/math] that is different from the true class, [math]\displaystyle{ x'=x \mathbf{-} \epsilon(sign(\nabla_xL(x,c^t(x)))) }[/math]. Here, [math]\displaystyle{ \nabla_xL() }[/math] is the gradient of the loss function with respect to the input, [math]\displaystyle{ \lambda }[/math] is a small gradient step and [math]\displaystyle{ sign() }[/math] is the sign of the gradient.
- An attacker may be allowed to use a single step of back-propagation (single step) or multiple (iterative) steps. Iterative attackers can generate more powerful adversarial images. Typically, to bound iterative attackers a distance measure is used.
In this paper the authors focus on the more difficult attacks; white-box iterative targeted and untargeted attacks.
Obfuscated Gradients
As gradients are used in the generation of white-box adversarial images, many defense strategies have focused on methods that mask gradients. If gradients are masked, they cannot be followed to generate adversarial images. The authors argue against this general approach by showing that it can be easily circumvented. To emphasize their point, they looked at white-box defenses proposed in ICLR 2018. Three types of gradient masking techniques were found:
- Shattered gradients: Non-differentiable operations are introduced into the model, causing a gradient to be nonexistent or incorrect.
- Stochastic gradients: A stochastic process is added into the model at test time, causing the gradients to become randomized.
- Vanishing Gradients : Very deep neural networks or those with recurrent connections are used. Because of the vanishing or exploding gradient problem common in these deep networks, effective gradients at the input are small and not very useful.
The Attacks
To circumvent these gradient masking techniques, the authors propose:
- Backward Pass Differentiable Approximation (BPDA): For defenses that introduce non-differentiable components, the authors replace it with an approximate function that is differentiable on the backward pass. In a white-box setting, the attacker has full access to any added non-linear transformation and can find its approximation.
- Expectation over Transformation [Athalye, 2017]: For defenses that add some form of test time randomness, the authors propose to use expectation over transformation technique in the backward pass. Rather than moving along the gradient every step, several gradients are sampled and the step is taken in the average direction. This can help with any stochastic misdirection from individual gradients. The technique is similar to using mini-batch gradient descent but applied in the construction of adversarial images.
- Re-parameterize the exploration space: For very deep networks that rely on vanishing or exploding gradients, the authors propose to re-parameterize and search over the range where the gradient does not explode/vanish.
Main Results
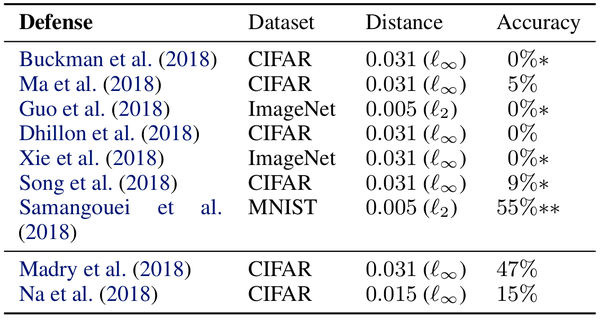
The table above summarizes the results of their attacks. Attacks are mounted on the same dataset each defense targeted. If multiple datasets were used, attacks were performed on the largest one. Two different distance metrics ([math]\displaystyle{ \ell_{\infty} }[/math] and [math]\displaystyle{ \ell_{2} }[/math]) were used in the construction of adversarial images. Distance metrics specify how much an adversarial image can vary from an original image. For [math]\displaystyle{ \ell_{\infty} }[/math] adversarial images, each pixel is allowed to vary by a maximum amount. For example, [math]\displaystyle{ \ell_{\infty}=0.031 }[/math] specifies that each pixel can vary by [math]\displaystyle{ 256*0.031=8 }[/math] from its original value. [math]\displaystyle{ \ell_{2} }[/math] distances specify the magnitude of the total distortion allowed over all pixels. For MNIST and CIFAR-10, untargeted adversarial images were constructed using the entire test set, while for Imagenet, 1000 test images were randomly selected and used to generate targeted adversarial images.
Standard models were used in evaluating the accuracy of defense strategies under the attacks,
- MNIST: 5-layer Convolutional Neural Network (99.3% top-1 accuracy)
- CIFAR-10: Wide-Resnet (95.0% top-1 accuracy)
- Imagenet: InceptionV3 (78.0% top-1 accuracy)
The last column shows the accuracies each defense method achieved over the adversarial test set. Except for [Madry, 2018], all defense methods could only achieve an accuracy of <10%. Furthermore, the accuracy of most methods was 0%. The results of [Samangoui,2018] (double asterisk), show that their approach was not as successful. The authors claim that is is a result of implementation imperfections but theoretically the defense can be circumvented using their proposed method.
The defense that worked - Adversarial Training [Madary, 2018]
As a defense mechanism, [Madry, 2018] proposes training the neural networks with adversarial images. Although this approach is previously known [Szegedy, 2013] in their formulation, the problem is setup in a more systematic way using a min-max formulation: \begin{align} \theta^* = \arg \underset{\theta} \min \mathop{\mathbb{E_x}} \bigg{[} \underset{\delta \in [-\epsilon,\epsilon]}\max L(x+\delta,y;\theta)\bigg{]} \end{align}
where [math]\displaystyle{ \theta }[/math] is the parameter of the model, [math]\displaystyle{ \theta^* }[/math] is the optimal set of parameters and [math]\displaystyle{ \delta }[/math] is a small perturbation to the input image [math]\displaystyle{ x }[/math] and is bounded by [math]\displaystyle{ [-\epsilon,\epsilon] }[/math].
Train proceeds in the following way. For each clean input image, a distorted version of the image is found by maximizing the inner maximization problem for a fixed number of iterations. Gradient steps are constrained to fall within the allowed range (projected gradient descent). Next, the classification problem is solved by minimizing the outer minimization problem.
This approach was shown to provide resilience to all types of adversarial attacks.
How to check for Obfuscated Gradients
For future defense proposals, it is recommended to avoid using masked gradients. To assist with this, the authors propose a set of conditions that can help identify if defense is relying on masked gradients:
- If weaker one-step attacks are performing better than iterative attacks.
- Black-box attacks can find stronger adversarial images compared with white-box attacks.
- Unbounded iterative attacks do not reach 100% success.
- If random brute force attempts are better than gradient based methods at finding adversarial images.
Recommendations for future defense methods to encourage reproducibility
Detailed Results
Non-obfuscated Gradients
Adversarial Training [Madry 2018]
Defence: Proposed by Goodfellow et al. (2014b), adversarial training solves a min-max game through a conceptually simple process: train on adversarial examples until the model learns to classify them correctly. The authors study the adversarial training approach of Madry et al. (2018) which for a given [math]\displaystyle{ \epsilon }[/math]-ball solves
which the authors of original paper, solve by the inner maximization problem by generating adversarial examples using projected gradient descent. The author's experiments were not able to invalidate the claims of the paper. The authors also mention that this approach does not cause obfuscated gradients and the original authors’ evaluation of this defense performs all of the tests for characteristic behaviours of obfuscated gradients that the authors of this paper list. Also, the authors note that (1) adversarial retraining has been shown to be difficult at a large scale like ImageNet, and (2) training exclusively on [math]\displaystyle{ l_\infty }[/math] adversarial examples provides only limited robustness to adversarial examples under other distortion metrics.
Cascade Adversarial Training [Na 2018]
Defence: Cascade adversarial machine learning approach is similar to the adversarial training approach mentioned above. The main difference is that instead of using iterative methods to generate adversarial examples at each mini-batch, a model is first trained, generate adversarial examples with iterative methods on that model, add those examples to training set, and then train a new model on the augmented dataset. Again, as above, the authors were unable to reduce the claims made by the paper even though the claims are a bit weaker in this case with 16% accuracy with [math]\displaystyle{ \epsilon }[/math] = .015, compared to over 70% at the same perturbation budget with adversarial training as in Madry et al. (2018).
Gradient Shattering
Thermometer Coding, [Buckman, 2018]
Defense: Inspired by the observation that neural networks learn linear boundaries between classes [Goodfellow, 2014] , [Buckman, 2018] sought to break this linearity by explicitly adding a highly non-linear transform at the input of their model. The non-linear transformation they chose was quantizing inputs to binary vectors. The quantization performed was termed thermometer encoding,
Given an image, for each pixel value [math]\displaystyle{ x_{i,j,c} }[/math], if an [math]\displaystyle{ l }[/math] dimensional thermometer code, the [math]\displaystyle{ kth }[/math] bit is given by: \begin{align} \tau(x_{i,j,c})_k = \bigg{\{}\begin{array}{ll} 1 \space if \thinspace x_{i,j,c} >k/l \\ 0 \space otherwise \\ \end{array} \end{align} Here it is assumed [math]\displaystyle{ x_{i,j,c} \in [0, 1] }[/math] and [math]\displaystyle{ i, j, c }[/math] are the row, column and channel index of the pixel respectively. This encoding is essentially like one-hot encoding, except all the points (not just one) greater than the target value are set to 1. This quantization technique preserves pairwise ordering between pixels.
On CIFAR-10, the model gave 50% accuracy against [math]\displaystyle{ \ell_\infty }[/math] adversarial images with [math]\displaystyle{ \epsilon=0.031 }[/math] attacks.
Attack: The authors attack this model using there BPDA approach. Given the non-linear transformation performed in the forward pass, [math]\displaystyle{ \tau(x) }[/math], they develop a differentiable counterpart, \begin{align} \hat{\tau}(x_{i,j,c})_k = \min ( \max (x_{i,j,c} - \frac{k}{l}), 1 ) \end{align} and use it in place of [math]\displaystyle{ \tau(x) }[/math] on the backward pass. With their modifications they were able to bring the accuracy of the model down to 0%.
Input Transformation, [Guo, 2018]
Defense:[Gou, 2018] investigated the effect of including different input transformation on the robustness to adversarial images. In particular, they found two techniques provided the greatest resistance: total variance minimization and image quilting. Total variance minimization is a technique that removes high frequency noise while preserving legitimate edges (good high frequency components). In image quilting, a large database of image patches from clean images is collected. At test time, input patches, that contain a lot of noise, are replaced with similar but clean patches from the data base.
Both techniques, removed perturbations from adversarial images which provides some robustness to adversarial attacks. Moreover, both approaches are non-differentiable which makes constructing white-box adversarial images difficult. Moreover, the techniques also include test time randomness as the modifications make are input dependent. The best model achieved 60% accuracy on adversarial images with [math]\displaystyle{ l_{2}=0.05 }[/math] perturbations.
Attack: The authors used the BPDA attack where the input transformations were replaced by an identity function. They were able to bring the accuracy of the model down to 0% under the same type of adversarial attacks.
Local Intrinsic Dimensionality, [Ma, 2018]
Defense Local intrinsic dimensionality (LID) is a distance-based metric that measures the similarity between points in a high dimensional space. Given a set of points, let the distance between sample [math]\displaystyle{ x }[/math] and its [math]\displaystyle{ ith }[/math] neighbor be [math]\displaystyle{ r_i(x) }[/math], then the LID under the choose distance metric is given by,
\begin{align} LID(x) = - \bigg{(} \frac{1}{k}\sum^k_{i=1}log \frac{r_i(x)}{r_k(x)} \bigg{)}^{-1} \end{align} where k is the number of nearest neighbors considered, [math]\displaystyle{ r_k(x) }[/math] is the maximum distance to any of the neighbors in the set k.
First, [math]\displaystyle{ L_2 }[/math] distances for all training and adversarial images. Next, the LID scores for each train and adversarial images were calculated. It was found that LID scores for adversarial images were significantly larger than those of clean images. Base on these results, the a separate classifier was created that can be used to detect adversarial inputs. [Ma, 2018] claim that this is not a defense method, but a method to study the properties of adversarial images.
Attack: Instead of attacking this method, the authors show that this method is not able to detect, and is therefore venerable to, attacks of the [Carlini and Wagner, 2017a] variety.
Stochastic Gradients
Stochastic Activation Pruning, [Dhillon, 2018]
Defense: [Dhillon, 2018] use test time randomness in their model to guard against adversarial attacks. Within a layer, the activities of component nodes are randomly dropped with a probability proportional to its absolute value. The rest of the activation are scaled up to preserve accuracies. This is akin to test time drop-out. This technique was found to drop accuracy slightly on clean images, but improved performance on adversarial images.
Attack: The authors used the expectation over transformation attack to get useful gradients out of the model. With their attack they were able to reduce the accuracy of this method down to 0% on CIFAR-10.
Mitigation Through Randomization, [Xie, 2018]
Defense: [Xie, 2018] Add a randomization layer to their model to help defend against adversarial attacks. For an input image of size [299,299], first the image is randomly re-scaled to [math]\displaystyle{ r \in [299,331] }[/math]. Next the image is zero-padded to fix the dimension of the modified input. This modified input is then fed into a regular classifier. The authors claim that is strategy can provide an accuracy of 32.8% against ensemble attack patterns (fixed distortions, but many of them which are picked randomly). Because of the introduced randomness, the authors claim the model builds some robustness to other types of attacks as well.
Attack: The EOT method was used to build adversarial images to attack this model. With their attack, the authors were able to bring the accuracy of this model down to 0% using [math]\displaystyle{ L_{\infty}(\epsilon=0.031) }[/math] perturbations.
Vanishing and Exploding Gradients
Pixel Defend, [Song, 2018]
Defense: [Song, 2018] argues that adversarial images lie in low probability regions of the data manifold. Therefore, one way to handle adversarial attacks is to project them back in the high probability regions before feeding them into a classifier. They chose to do this by using a generative model (pixelCNN) in a denoising capacity. A PixelCNN model directly estimates the conditional probability of generating an image pixel by pixel [Van den Oord, 2016],
\begin{align} p(\mathbf{x}= \prod_{i=1}^{n^2} p(x_i|x_0,x_1 ....x_{i-1})) \end{align}
The reason for choosing this model is the long iterative process of generation. In the backward pass, following the gradient all the way to the input would not be possible because of the vanishing/exploding gradient problem of deep networks. The proposed model was able to obtain an accuracy of 46% on CIFAR-10 images with [math]\displaystyle{ l_{\infty} (\epsilon=0.031) }[/math] perturbations.
Attack: The model was attacked using the BPDA technique where back-propagating though the pixelCNN was replaced with an identity function. With this apporach, the authors were able to bring down the accuracy to 9% under the same kind of perturbations.
Defense-GAN, [Samangouei, 2018]
Conclusion
In this paper, it was found that gradient masking is a common technique used by many defense proposal that claim to be robust against a very difficult class of adversarial attacks; white-box, iterative attacks. However, the authors found that they can be easily circumvented. Three attack methods are presented that were able to defeat 7 out of the 8 defense proposal accepted in the 2018 ICLR conference for these types of attacks.
Some future work that can come out of this paper includes avoiding relying on obfuscated gradients for perceived robustness and use the evaluation approach to detect when the attach occurs. Early categorization of attacks using some supervised techniques can also help in critical evaluation of incoming data.
Critique
- The third attack method, reparameterization of the input distortion search space was presented very briefly and at a very high level. Moreover, the one defense proposal they chose to use it against, [Samangouei, 2018] prove to be resilient against the attack. The authors had to resort to one of their other methods to circumvent the defense.
- The BPDA and reparameterization attacks require intrinsic knowledge of the networks. This information is not likely to be available to external users of a network. Most likely, the use-case for these attacks will be in-house to develop more robust networks. This also means that it is still possible to guard against adversarial attack using gradient masking techniques, provided the details of the network are kept secret.
- The BPDA algorithm requires replacing a non-linear part of the model with a differentiable approximation. Since different networks are likely to use different transformations, this technique is not plug-and-play. For each network, the attack needs to be manually constructed.
Other Sources
References
- [Madry, 2018] Madry, A., Makelov, A., Schmidt, L., Tsipras, D. and Vladu, A., 2017. Towards deep learning models resistant to adversarial attacks. arXiv preprint arXiv:1706.06083.
- [Buckman, 2018] Buckman, J., Roy, A., Raffel, C. and Goodfellow, I., 2018. Thermometer encoding: One hot way to resist adversarial examples.
- [Guo, 2018] Guo, C., Rana, M., Cisse, M. and van der Maaten, L., 2017. Countering adversarial images using input transformations. arXiv preprint arXiv:1711.00117.
- [Xie, 2018] Xie, C., Wang, J., Zhang, Z., Ren, Z. and Yuille, A., 2017. Mitigating adversarial effects through randomization. arXiv preprint arXiv:1711.01991.
- [song, 2018] Song, Y., Kim, T., Nowozin, S., Ermon, S. and Kushman, N., 2017. Pixeldefend: Leveraging generative models to understand and defend against adversarial examples. arXiv preprint arXiv:1710.10766.
- [Szegedy, 2013] Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan, D., Goodfellow, I. and Fergus, R., 2013. Intriguing properties of neural networks. arXiv preprint arXiv:1312.6199.
- [Samangouei, 2018] Samangouei, P., Kabkab, M. and Chellappa, R., 2018. Defense-GAN: Protecting classifiers against adversarial attacks using generative models. arXiv preprint arXiv:1805.06605.
- [van den Oord, 2016] van den Oord, A., Kalchbrenner, N., Espeholt, L., Vinyals, O. and Graves, A., 2016. Conditional image generation with pixelcnn decoders. In Advances in Neural Information Processing Systems (pp. 4790-4798).
- [Athalye, 2017] Athalye, A. and Sutskever, I., 2017. Synthesizing robust adversarial examples. arXiv preprint arXiv:1707.07397.
- [Ma, 2018] Ma, Xingjun, Bo Li, Yisen Wang, Sarah M. Erfani, Sudanthi Wijewickrema, Michael E. Houle, Grant Schoenebeck, Dawn Song, and James Bailey. "Characterizing adversarial subspaces using local intrinsic dimensionality." arXiv preprint arXiv:1801.02613 (2018).