Neural Speed Reading via Skim-RNN
Group
Mingyan Dai, Jerry Huang, Daniel Jiang
Introduction
In Natural Language Processing, recurrent neural networks (RNNs) are a common architecture used to sequentially ‘read’ input tokens and output a distributed representation for each token. By recurrently updating the hidden state of the neural network, a RNN can inherently require the same computational cost across time. However, when it comes to processing input tokens, it is usually the case that some tokens are less important to the overall representation of a piece of text or a query when compared to others. In particular, when considering question answering, many times the neural network will encounter parts of a passage that is irrelevant when it comes to answering a query that is being asked.
Model
In this paper, the authors introduce a model called 'skim-RNN', which takes advantage of ‘skimming’ less important tokens or pieces of text rather than ‘skipping’ them entirely. This models the human ability to skim through passages, or to spend less time reading parts do not affect the reader’s main objective. While this leads to a loss in the comprehension rate of the text [1], it greatly reduces the amount of time spent reading by not focusing on areas which will not significantly affect efficiency when it comes to the reader's objective.
'Skim-RNN' works by rapidly determining the significance of each input and spending less time processing unimportant input tokens by using a smaller RNN to update only a fraction of the hidden state. When the decision is to ‘fully read’, that is to not skim the text, Skim-RNN updates the entire hidden state with the default RNN cell. Since the hard decision function (‘skim’ or ‘read’) is non-differentiable, the authors use a gumbel-softmax [2] to estimate the gradient of the function, rather than traditional methods such as REINFORCE (policy gradient)[3]. The switching mechanism between the two RNN cells enables Skim-RNN to reduce the total number of float operations (Flop reduction, or Flop-R). When the skimming rate is high, which often leads to faster inference on CPUs, which makes it very useful for large-scale products and small devices.
The Skim-RNN has the same input and output interfaces as standard RNNs, so it can be conveniently used to speed up RNNs in existing models. In addition, the speed of Skim-RNN can be dynamically controlled at inference time by adjusting a parameter for the threshold for the ‘skim’ decision.
Implementation
A Skim-RNN consists of two RNN cells, a default (big) RNN cell of hidden state size [math]\displaystyle{ d }[/math] and small RNN cell of hidden state size [math]\displaystyle{ d' }[/math], where [math]\displaystyle{ d }[/math] and [math]\displaystyle{ d' }[/math] are parameters defined by the user and [math]\displaystyle{ d \ll d' }[/math]. This follows the fact that there should be a small RNN cell defined for when text is meant to be skimmed and a larger one for when the text should be processed as normal.
Each RNN cell will have its own set of weights and bias as well as be any variant of an RNN. There is no requirement on how the RNN itself is structured, rather the core concept is to allow the model to dynamically make a decision as to which cell to use when processing input tokens. Note that skipping text can be incorporated by setting [math]\displaystyle{ d' }[/math] to 0, which means that when the input token is deemed irrelevant to a query or classification task, nothing about the information in the token is retained within the model.
Experimental results suggest that this model is faster than using a single large RNN to process all input tokens, as the smaller RNN requires fewer floating point operations to process the token. Additionally, higher accuracy and computational efficiency are achieved.
Inference
At each time step [math]\displaystyle{ t }[/math], the Skim-RNN unit takes in an input [math]\displaystyle{ {\bf x}_t \in \mathbb{R}^d }[/math] as well as the previous hidden state [math]\displaystyle{ {\bf h}_{t-1} \in \mathbb{R}^d }[/math] and outputs the new state [math]\displaystyle{ {\bf h}_t }[/math] (although the dimensions of the hidden state and input are the same, this process holds for different sizes as well). In the Skim-RNN, there is a hard decision that needs to be made whether to read or skim the input, although there could be potential to include options for multiple levels of skimming.
The decision to read or skim is done using a multinomial random variable [math]\displaystyle{ Q_t }[/math] over the probability distribution of choices [math]\displaystyle{ {\bf p}_t }[/math], where
[math]\displaystyle{ {\bf p}_t = \text{softmax}(\alpha({\bf x}_t, {\bf h}_{t-1})) = \text{softmax}({\bf W}[{\bf x}_t; {\bf h}_{t-1}]+{\bf b}) \in \mathbb{R}^k }[/math]
where [math]\displaystyle{ {\bf W} \in \mathbb{R}^{k \times 2d} }[/math], [math]\displaystyle{ {\bf b} \in \mathbb{R}^{k} }[/math] are weights to be learned and [math]\displaystyle{ [{\bf x}_t; {\bf h}_{t-1}] \in \mathbb{R}^{2d} }[/math] indicates the row concatenation of the two vectors. In this case [math]\displaystyle{ \alpha }[/math] can have any form as long as the complexity of calculating it is less than [math]\displaystyle{ O(d^2) }[/math]. Letting [math]\displaystyle{ {\bf p}^1_t }[/math] indicate the probability for fully reading and [math]\displaystyle{ {\bf p}^2_t }[/math] indicate the probability for skimming the input at time [math]\displaystyle{ t }[/math], it follows that the decision to read or skim can be modelled using a random variable [math]\displaystyle{ Q_t }[/math] by sampling from the distribution [math]\displaystyle{ {\bf p}_t }[/math] and
[math]\displaystyle{ Q_t \sim \text{Multinomial}({\bf p}_t) }[/math]
Without loss of generality, we can define [math]\displaystyle{ Q_t = 1 }[/math] to indicate that the input will be read while [math]\displaystyle{ Q_t = 2 }[/math] indicates that it will be skimmed. Reading requires applying the full RNN on the input as well as the previous hidden state to modify the entire hidden state, while skimming only modifies part of the prior hidden state.
[math]\displaystyle{ {\bf h}_t = \begin{cases} f({\bf x}_t, {\bf h}_{t-1}) & Q_t = 1\\ [f'({\bf x}_t, {\bf h}_{t-1});{\bf h}_{t-1}(d'+1:d)] & Q_t = 2 \end{cases} }[/math]
where [math]\displaystyle{ f }[/math] is a full RNN with output of dimension [math]\displaystyle{ d }[/math] and [math]\displaystyle{ f' }[/math] is a smaller RNN with [math]\displaystyle{ d' }[/math]-dimensional output. This has advantage that when the model decides to skim, then the computational complexity of that step is only [math]\displaystyle{ O(d'd) }[/math], which is much smaller than [math]\displaystyle{ O(d^2) }[/math] due to previously defining [math]\displaystyle{ d' \ll d }[/math].
Training
Since the expected loss/error of the model is a random variable that depends on the sequence of random variables [math]\displaystyle{ \{Q_t\} }[/math], the loss is minimized with respect to the distribution of the variables. Defining the loss to be minimized while conditioning on a particular sequence of decisions
[math]\displaystyle{ L(\theta\vert Q) }[/math]
where [math]\displaystyle{ Q=Q_1\dots Q_T }[/math] is a sequence of decisions of length [math]\displaystyle{ T }[/math], then the expected loss o ver the distribution of the sequence of decisions is
[math]\displaystyle{ \mathbb{E}[L(\theta)] = \sum_{Q} L(\theta\vert Q)P(Q) = \sum_Q L(\theta\vert Q) \Pi_j {\bf p}_j^{Q_j} }[/math]
Since calculating [math]\displaystyle{ \delta \mathbb{E}_{Q_t}[L(\theta)] }[/math] directly is rather infeasible, it is possible to approximate the gradients with a gumbel-softmax distribution [2]. Reparameterizing [math]\displaystyle{ {\bf p}_t }[/math] as [math]\displaystyle{ {\bf r}_t }[/math], then the back-propagation can flow to [math]\displaystyle{ {\bf p}_t }[/math] without being blocked by [math]\displaystyle{ Q_t }[/math] and the approximation can arbitrarily approach [math]\displaystyle{ Q_t }[/math] by controlling the parameters. The reparameterized distribution is therefore
[math]\displaystyle{ {\bf r}_t^i = \frac{\text{exp}(\log({\bf p}_t^i + {g_t}^i)/\tau)}{\sum_j\text{exp}(\log({\bf p}_t^j + {g_t}^j)/\tau)} }[/math]
where [math]\displaystyle{ {g_t}^i }[/math] is an independent sample from a [math]\displaystyle{ \text{Gumbel}(0, 1) = -\log(-\log(\text{Uniform}(0, 1)) }[/math] random variable and [math]\displaystyle{ \tau }[/math] is a parameter that represents a temperature. Then it can be rewritten that
[math]\displaystyle{ {\bf h}_t = \sum_i {\bf r}_t^i {\bf \tilde{h}}_t }[/math]
where [math]\displaystyle{ {\bf \tilde{h}}_t }[/math] is the previous equation for [math]\displaystyle{ {\bf h}_t }[/math]. The temperature parameter gradually decreases with time, and [math]\displaystyle{ {\bf r}_t^i }[/math] becomes more discrete as it approaches 0.
A final addition to the model is to encourage skimming when possible. Therefore an extra term related to the negative log probability of skimming and the sequence length. Therefore the final loss function used for the model is denoted by
[math]\displaystyle{ L'(\theta) =L(\theta) + \gamma \cdot\frac{1}{T} \sum_i -\log({\bf \tilde{p}}^i_t) }[/math]
where [math]\displaystyle{ \gamma }[/math] is a parameter used to control the ratio between the main loss function and the negative log probability of skimming.
Experiment
The effectiveness of Skim-RNN was measured in terms of accuracy and float operation reduction on four classification tasks and a question answering task. These tasks were chosen because they do not require one’s full attention to every detail of the text, but rather ask for capturing the high-level information (classification) or focusing on specific portion (QA) of the text, which a common context for speed reading. The tasks themselves are listed in the table below.
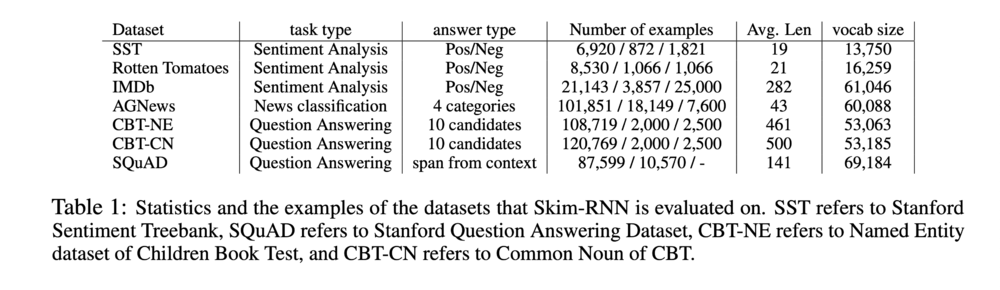
Classification Tasks
In a language classification task, the input was a sequence of words and the output was the vector of categorical probabilities. Each word is embedded into a [math]\displaystyle{ d }[/math]-dimensional vector. We initialize the vector with GloVe [4] to form representations of the words and use those as the inputs for a long short-term memory (LSTM) architecture. A linear transformation on the last hidden state of the LSTM and then a softmax function was applied to obtain the classification probabilities. Adam [5] was used for optimization, with initial learning rate of 0.0001. For Skim-LSTM, [math]\displaystyle{ \tau = \max(0.5, exp(−rn)) }[/math] where [math]\displaystyle{ r = 1e-4 }[/math] and [math]\displaystyle{ n }[/math] is the global training step, following [2]. We experiment on different sizes of big LSTM ([math]\displaystyle{ d \in \{100, 200\} }[/math]) and small LSTM ([math]\displaystyle{ d' \in \{5, 10, 20\} }[/math]) and the ratio between the model loss and the skim loss ([math]\displaystyle{ \gamma\in \{0.01, 0.02\} }[/math]) for Skim-LSTM. The batch sizes used were 32 for SST and Rotten Tomatoes, and 128 for others. For all models, early stopping was used when the validation accuracy did not increase for 3000 global steps.
Results
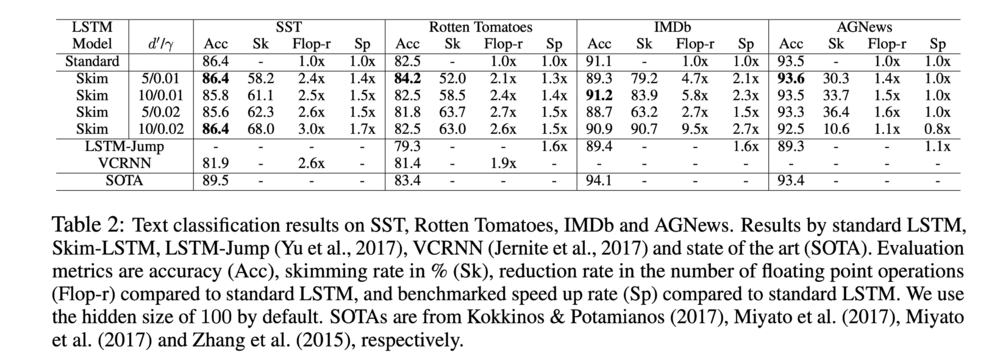
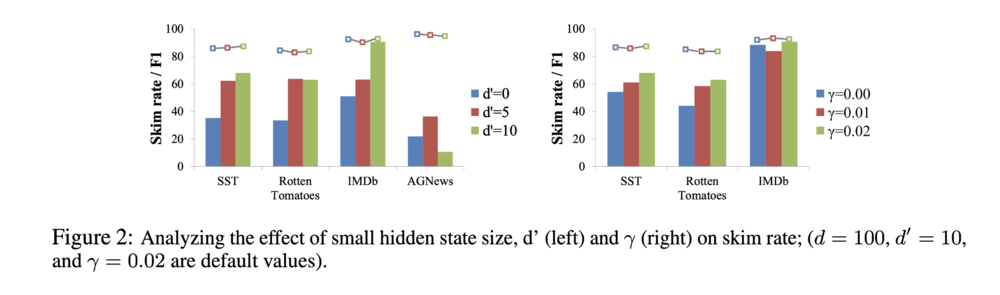
Table 2 shows the accuracy and the computational cost of the Skim-RNN model compared with other standard models. It is evident that the Skim-RNN model produces a speed-up on the computational complexity of the task while maintaining a high degree of accuracy. Figure 2 meanwhile demonstrates the effect of varying the size of the small hidden state as well as the parameter [math]\displaystyle{ \gamma }[/math] on the accuracy and computational cost.

Table 3 shows an example of a classification task over a IMDb dataset, where Skim-RNN with [math]\displaystyle{ d = 200 }[/math], [math]\displaystyle{ d' = 10 }[/math], and [math]\displaystyle{ \gamma = 0.01 }[/math] correctly classifies it with high skimming rate (92%). The goal was to classify the review as either positive or negative. The black words are skimmed, and blue words are fully read. The skimmed words are clearly irrelevant and the model learns to only carefully read the important words, such as ‘liked’, ‘dreadful’, and ‘tiresome’.
Question Answering Task
In Stanford Question Answering Dataset, the task was to locate the answer span for a given question in a context paragraph. The effectiveness of Skim-RNN for SQuAD was evaluated using two different models: LSTM+Attention and BiDAF [6]. The first model was inspired by most then-present QA systems consisting of multiple LSTM layers and an attention mechanism. This type of model is complex enough to reach reasonable accuracy on the dataset, and simple enough to run well-controlled analyses for the Skim-RNN. The second model wan an open-source model designed for SQuAD, used primarily to show that Skim-RNN could replace RNN in existing complex systems.
Training
Adam was used with an initial learning rate of 0.0005. For stable training, the model was pretrained with a standard LSTM for the first 5k steps , and then fine-tuned with Skim-LSTM.
Results
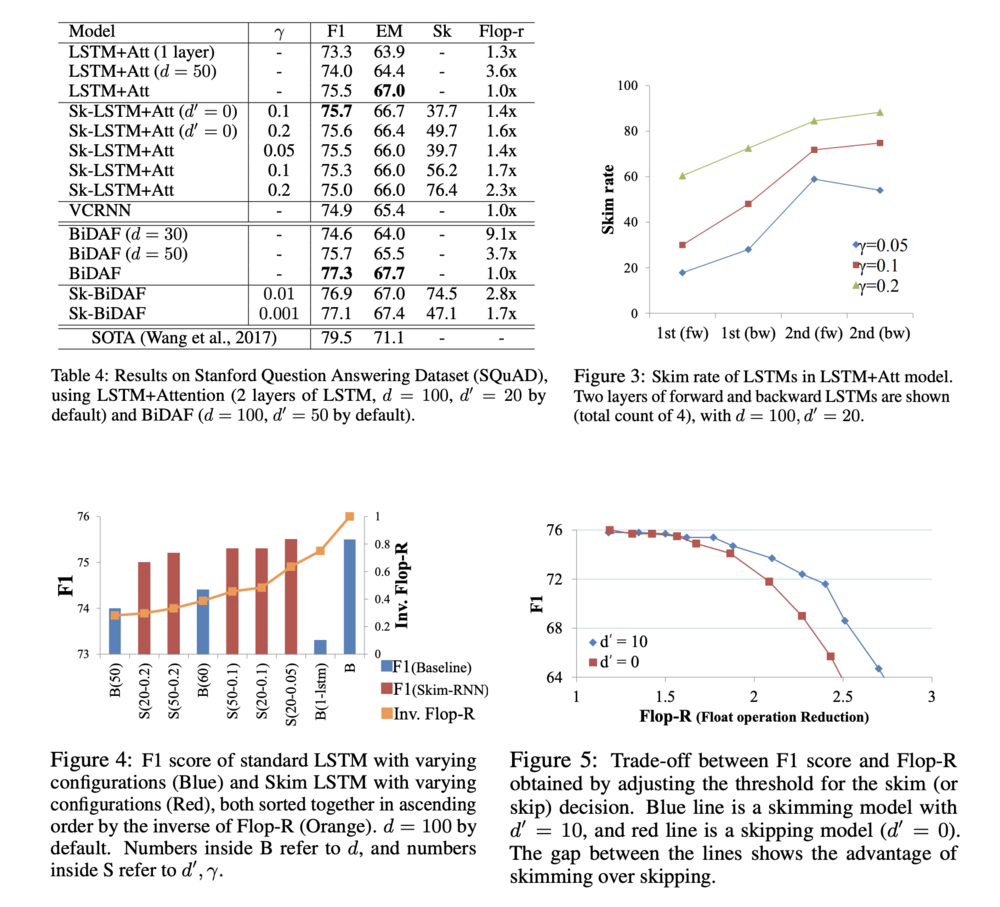
Table 4 shows the accuracy (F1 and EM) of LSTM+Attention and Skim-LSTM+Attention models as well as VCRNN [7]. It can be observed from the table that the skimming models achieve higher or similar accuracy scores compared to the non-skimming models while also reducing the computational cost by more than 1.4 times. In addition, decreasing layers (1 layer) or hidden size ([math]\displaystyle{ d=5 }[/math]) improved the computational cost but significantly decreases the accuracy compared to skimming. The table also shows that replacing LSTM with Skim-LSTM in an existing complex model (BiDAF) stably gives reduced computational cost without losing much accuracy (only 0.2% drop from 77.3% of BiDAF to 77.1% of Sk-BiDAF with [math]\displaystyle{ \gamma = 0.001 }[/math]).
An explanation for this trend that was given is that the model is more confident about which tokens are important at the second layer. Second, higher [math]\displaystyle{ \gamma }[/math] values lead to higher skimming rate, which agrees with its intended functionality.
Figure 4 shows the F1 score of LSTM+Attention model using standard LSTM and Skim LSTM, sorted in ascending order by Flop-R (computational cost). While models tend to perform better with larger computational cost, Skim LSTM (Red) outperforms standard LSTM (Blue) with comparable computational cost. It can also be seen that the computational cost of Skim-LSTM is more stable across different configurations and computational cost. Moreover, increasing the value of [math]\displaystyle{ \gamma }[/math] for Skim-LSTM gradually increases the skipping rate and Flop-R, while it also led to reduced accuracy.
Runtime Benchmark
The details of the runtime benchmarks for LSTM and Skim-LSTM, are used estimate the speed up of Skim-LSTM-based models in the experiments, are also discussed. A CPU-based benchmark was assumed to be the default benchmark, which has direct correlation with the number of float operations that can be performed per second. As mentioned previously, the speed-up results in Table 2 (as well as Figure 7) are benchmarked using Python (NumPy), instead of popular frameworks such as TensorFlow or PyTorch.
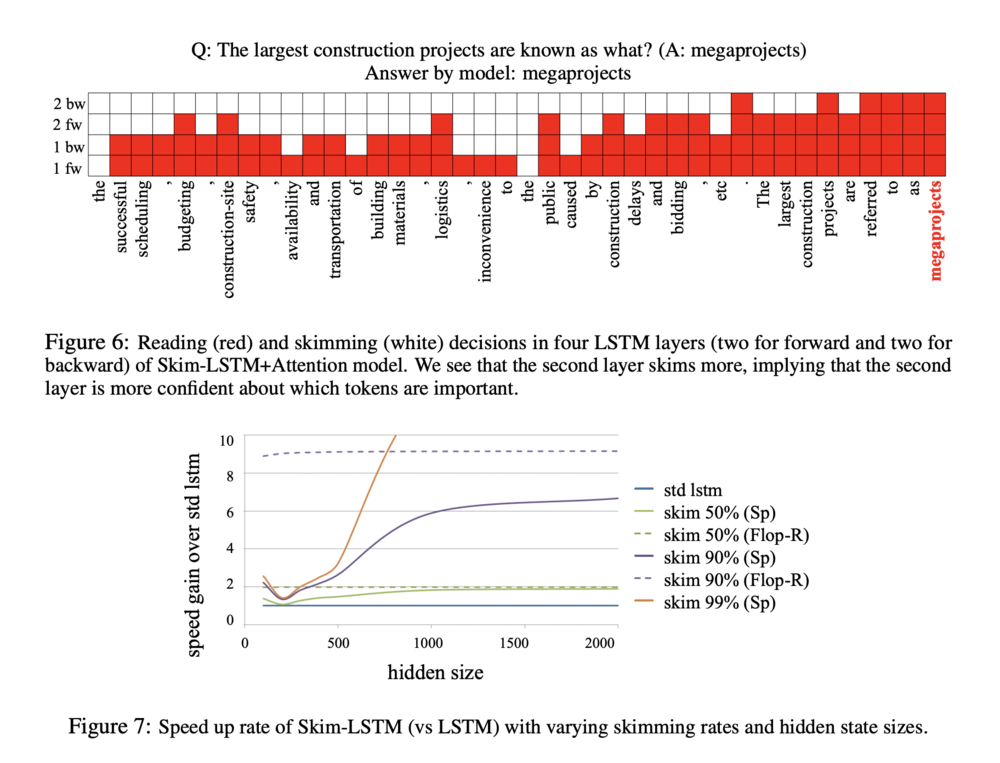
Figure 7 shows the relative speed gain of Skim-LSTM compared to standard LSTM with varying hidden state size and skim rate. NumPy was used, with the inferences run on a single thread of CPU. The ratio between the reduction of the number of float operations (Flop-R) of LSTM and Skim-LSTM was plotted, with the ratio acting as a theoretical upper bound of the speed gain on CPUs. From here, it can be noticed that there is a gap between the actual gain and the theoretical gain in speed, with the gap being larger with more overhead of the framework, or more parallelization. The gap also decreases as the hidden state size increases because the the overhead becomes negligible with very large matrix operations. This indicates that Skim-RNN provide greater benefits for RNNs with larger hidden state size.
Results
The results clearly indicate that the Skim-RNN model provides features that are suitable for general reading tasks, which include classification and question answering. While the tables indicate that minor losses in accuracy occasionally did result when parameters were set at specific values, they were not minor and were acceptable given the improvement in runtime.
An important advantage of Skim-RNN is that the skim rate (and thus computational cost) can be dynamically controlled at inference time by adjusting the threshold for ‘skim’ decision probability [math]\displaystyle{ {\bf p}^1_t }[/math]. Figure 5 shows the trade-off between the accuracy and computational cost for two settings, confirming the importance of skimming ([math]\displaystyle{ d' \gt 0 }[/math]) compared to skipping ([math]\displaystyle{ d' = 0 }[/math]).
Figure 6 shows that the model does not skim when the input seems to be relevant to answering the question, which was as expected by the design of the model. In addition, the LSTM in second layer skims more than that in the first layer mainly because the second layer is more confident about the importance of each token.
Conclusion
A Skim-RNN can offer better latency results on a CPU compared to a standard RNN on a GPU, with lower computational cost, as demonstrated through the results of this study. Future work (as stated by the authors) involves using Skim-RNN for applications that require much higher hidden state size, such as video understanding, and using multiple small RNN cells for varying degrees of skimming. Further, since it has the same input and output interface as a regular RNN it can replace RNNs in existing applications.
Critiques
1. It seems like Skim-RNN is using the not full RNN of processing words that are not important thus can increase speed in some very particular circumstances (ie, only small networks). The extra model complexity did slow down the speed while trying to "optimizing" the efficiency and sacrifice part of accuracy while doing so. It is only trying to target a very specific situation (classification/question-answering) and made comparisons only with the baseline LSTM model. It would be definitely more persuasive if the model can compare with some of the state of art nn models.
2. This model of Skim-RNN is pretty good to extract binary classification type of text, thus it would be interesting for this to be applied to stock market news analyzing. For example a press release from a company can be analyzed quickly using this model and immediately give the trader a positive or negative summary of the news. Would be beneficial in trading since time and speed is an important factor when executing a trade.
References
[1] Patricia Anderson Carpenter Marcel Adam Just. The Psychology of Reading and Language Comprehension. 1987.
[2] Eric Jang, Shixiang Gu, and Ben Poole. Categorical reparameterization with gumbel-softmax. In ICLR, 2017.
[3] Ronald J Williams. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine learning, 8(3-4):229–256, 1992.
[4] Jeffrey Pennington, Richard Socher, and Christopher D Manning. Glove: Global vectors for word representation. In EMNLP, 2014.
[5] Diederik Kingma and Jimmy Ba. Adam: A method for stochastic optimization. In ICLR, 2015.
[6] Minjoon Seo, Aniruddha Kembhavi, Ali Farhadi, and Hannaneh Hajishirzi. Bidirectional attention flow for machine comprehension. In ICLR, 2017a.
[7] Yacine Jernite, Edouard Grave, Armand Joulin, and Tomas Mikolov. Variable computation in recurrent neural networks. In ICLR, 2017.