Loss Function Search for Face Recognition
Presented by
Jan Lau, Anas Mahdi, Will Thibault, Jiwon Yang
Introduction
Face recognition is a technology that can label a face to a specific identity. The process involves two tasks: 1. Identifying and classifying a face to a certain identity and 2. Verifying if this face and another face map to the same identity. Loss functions play an important role in evaluating how well the prediction models the given data. In the application of face recognition, they are used for training convolutional neural networks (CNNs) with discriminative features. However, traditional softmax loss lacks the power of feature discrimination. To solve this problem, a center loss was developed to learn centers for each identity to enhance the intra-class compactness.
Hence, the paper introduced a new loss function which can reduce the softmax probability. Softmax probability is the probability for each class. It contains a vector of values that add up to 1 while ranging between 0 and 1. Cross-entropy loss is the negative log of the probabilities. When softmax probability is combined with cross-entropy loss in the last fully connected layer of the CNN, it yields the softmax loss function:
Specifically for face recognition, [math]\displaystyle{ L_1 }[/math] is modified such that [math]\displaystyle{ w^T_yx }[/math] is normalized and [math]\displaystyle{ s }[/math] represents the magnitude of [math]\displaystyle{ w^T_yx }[/math]:
This function is crucial in face recognition because it is used for enhancing feature discrimination. While there are different variations of the softmax loss function, they build upon the same structure as the equation above. Some of these variations will be discussed in detail in the later sections.
In this paper, the authors first identified that reducing the softmax probability is a key contribution to feature discrimination and designed two design search spaces (random and reward-guided method). They then evaluated their Random-Softmax and Search-Softmax approaches by comparing the results against other face recognition algorithms using nine popular face recognition benchmarks.
Previous Work
Margin-based (angular, additive, additive angular margins) soft-max loss functions are important in learning discriminative features in face recognition. There have been hand-crafted methods previously developed that require much efforts such as A-softmax, V-softmax, AM-Softmax, and Arc-softmax. Li et al. proposed an AutoML for loss function search method also known as AM-LFS from a hyper-parameter optimization perspective [2]. It automatically determines the search space by leveraging reinforcement learning to the search loss functions during the training process, though the drawback is the complex and unstable search space.
Motivation
Previous algorithms for facial recognition frequently rely on CNNs that may include metric learning loss functions such as contrastive loss or triplet loss. Without sensitive sample mining strategies, the computational cost for these functions was high. This drawback prompts the redesign of classical softmax loss that cannot discriminate features. Multiple softmax loss functions have since been developed, and including margin-based formulations, they often require fine-tuning of parameters and are susceptible to instability. Therefore, researchers need to put in a lot of effort in creating their method in the large design space. AM-LFS takes an optimization approach for selecting hyperparameters for the margin-based softmax functions, but its aforementioned drawbacks are caused by the lack of direction in designing the search space.
To solve the issues associated with hand-tuned softmax loss functions and AM-LFS, the authors attempt to reduce the softmax probability to improve feature discrimination when using margin-based softmax loss functions. The development of margin-based softmax loss with only one parameter required and an improved search space using a reward-based method which allows the authors to determine the best option for their loss function.
Problem Formulation
Analysis of Margin-based Softmax Loss
Based on the softmax probability and the margin-based softmax probability, the following function can be developed [1]:
[math]\displaystyle{ a }[/math] is considered as a modulating factor and [math]\displaystyle{ h{(a,p)}=\frac{1}{ap+(1-a)} \in (0,1] }[/math] is a modulating function [1]. Therefore, regardless of the margin function ([math]\displaystyle{ f }[/math]), the minimization of the softmax probability will ensure success.
Compared to AM-LFS, this method involves only one parameter ([math]\displaystyle{ a }[/math]) that is also constrained, versus AM-LFS which has 2M parameters without constraints that specify the piecewise linear functions the method requires. Also, the piecewise linear functions of AM-LFS ([math]\displaystyle{ p_m={a_i}p+b_i }[/math]) may not be discriminative because it could be larger than the softmax probability.
Random Search
Unified formulation [math]\displaystyle{ L_5 }[/math] is generated by inserting a simple modulating function [math]\displaystyle{ h{(a,p)}=\frac{1}{ap+(1-a)} }[/math] into the original softmax loss. It can be written as below [1]:
This encourages the feature margin between different classes and has the capability of feature discrimination. This leads to defining the search space as the choice of [math]\displaystyle{ h{(a,p)} }[/math] whose impacts on the training procedure are decided by the modulating factor [math]\displaystyle{ a }[/math]. In order to validate the unified formulation, a modulating factor is randomly set at each training epoch. This is noted as Random-Softmax in this paper.
Reward-Guided Search
Unlike supervised learning, reinforcement learning (RL) is a behavioral learning model. It does not need to have input/output labelled and it does not need a sub-optimal action to be explicitly corrected. The algorithm receives feedback from the data to achieve the best outcome. The system has an agent that guides the process by taking an action that maximizes the notion of cumulative reward [3]. The process of RL is shown in figure 1. The equation of the cumulative reward function is:
where [math]\displaystyle{ G_t }[/math] = cumulative reward, [math]\displaystyle{ R_t }[/math] = immediate reward, and [math]\displaystyle{ R_T }[/math] = end of episode.
[math]\displaystyle{ G_t }[/math] is the sum of immediate rewards from arbitrary time [math]\displaystyle{ t }[/math]. It is a random variable because it depends on the immediate reward which depends on the agent action and the environment's reaction to this action.

The reward function is what guides the agent to move in a certain direction. As mentioned above, the system receives feedback from the data to achieve the best outcome. This is caused by the reward being edited based on the feedback it receives when a task is completed [5].
In this paper, RL is being used to generate a distribution of the hyperparameter [math]\displaystyle{ \mu }[/math] for the SoftMax equation using the reward function. [math]\displaystyle{ \mu }[/math] updates after each epoch from the reward function.
Optimization
Calculating the reward involves a standard bi-level optimization problem, which involves a hyperparameter ({[math]\displaystyle{ a_1,a_2,…,a_B }[/math]}) that can be used for minimizing one objective function while maximizing another objective function simultaneously:
In this case, the loss function takes the training set [math]\displaystyle{ S_t }[/math] and the reward function takes the validation set [math]\displaystyle{ S_v }[/math]. The weights [math]\displaystyle{ w }[/math] are trained such that the loss function is minimized while the reward function is maximized. The calculated reward for each model ({[math]\displaystyle{ M_{we1},M_{we2},…,M_{weB} }[/math]}) yields the corresponding score, then the algorithm chooses the one with the highest score for model index selection. With the model containing the highest score being used in the next epoch, this process is repeated until the training reaches convergence. In the end, the algorithm takes the model with the highest score without retraining.
Results and Discussion
Data Preprocessing
The training datasets consisted of cleaned versions of CASIA-WebFace and MS-Celeb-1M-v1c to remove the impact of noisy labels in the original sets. Furthermore, there were a total of 15,414 identities that overlapped between the testing and training datasets. These were removed from the training sets.
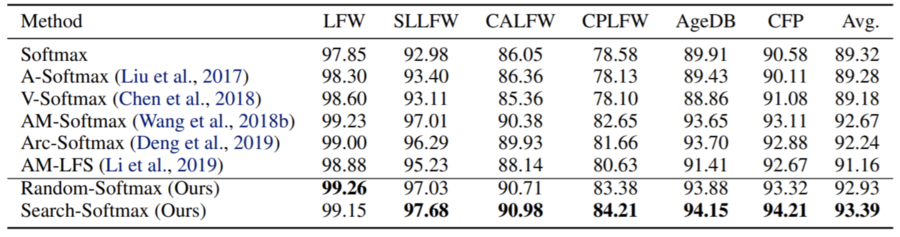
Results on LFW, SLLFW, CALFW, CPLFW, AgeDB, DFP
For LFW, there is not a noticeable difference between the algorithms proposed in this paper and the other algorithms, however, AM-Softmax achieved higher results than Search-Softmax. Random-Softmax achieved the highest results by 0.03%.
Random-Softmax outperforms baseline Soft-max and is comparable to most of the margin-based softmax. Search-Softmax boost the performance and better most methods specifically when training CASIA-WebFace-R data set, it achieves 0.72% average improvement over AM-Softmax. The reason the model proposed by the paper gives better results is because of their optimization strategy which helps boost the discimination power. Also the sampled candidate from the paper’s proposed search space can well approximate the margin-based loss functions. More tests need to happen to more complicated protocols to test the performance further. Not a lot of improvement has been shown on those test sets, since they are relatively simple and the performance of all the methods on these test sets are near saturation. The following table gives a summary of the performance of each model.
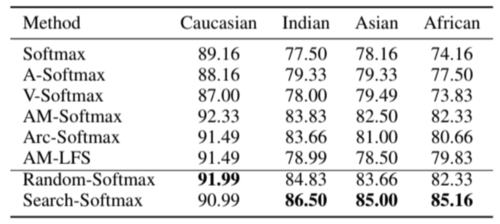
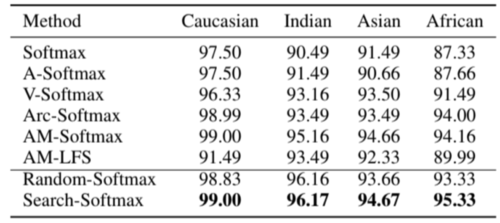
Results on RFW
The RFW dataset measures racial bias which consists of Caucasian, Indian, Asian, and African. Using this as the test set, Random-softmax and Search-softmax performed better than the other methods. Random-softmax outperforms the baseline softmax by a large margin which means reducing the softmax probability will enhance the feature discrimination for face recognition. It is also observed that the reward guided search-softmax method is more likely to enhance the discriminative feature learning resulting in higher performance as shown in Table 2 and Table 3.
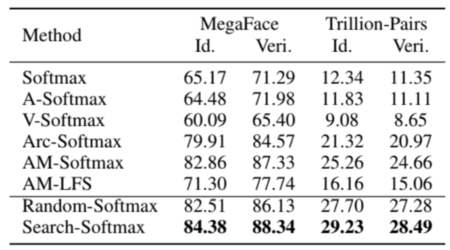
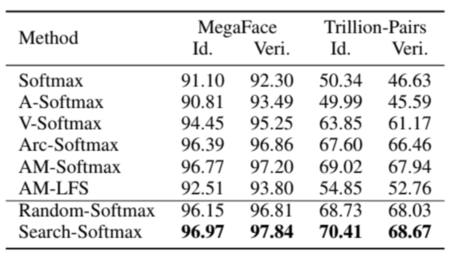
Results on MegaFace and Trillion-Pairs
The different loss functions are tested again with more complicated protocols. The identification (Id.) Rank-1 and the verification (Veri.) with the true positive rate (TPR) at low false acceptance rate (FAR) at [math]\displaystyle{ 1e-3 }[/math] on MegaFace, the identification TPR@FAR = [math]\displaystyle{ 1e-6 }[/math] and the verification TPR@FAR = [math]\displaystyle{ 1e-9 }[/math] on Trillion-Pairs are reported on Table 4 and 5.
On the test sets MegaFace and Trillion-Pairs, Search-softmax achieves the best performance over all other alternative methods. On MegaFace, Search-softmax beat the best competitor AM-softmax by a large margin. It also outperformed AM-LFS due to new designed search space.
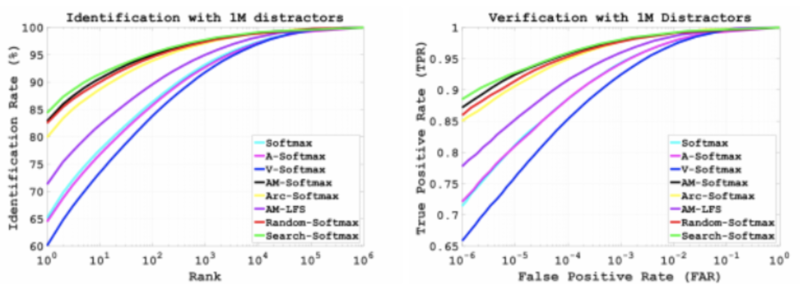
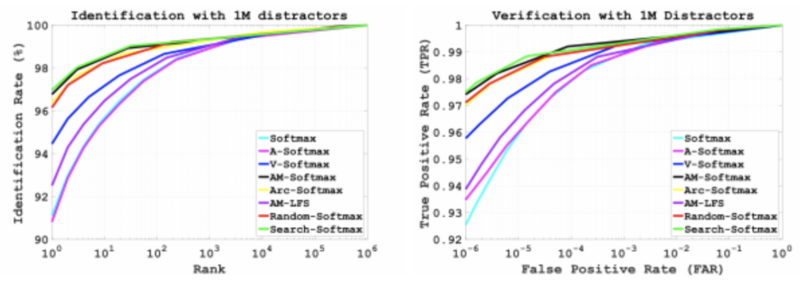
From the CMC curves and ROC curves in Figure 2, similar trends are observed at other measures. There is a same trend on Trillion-Pairs where Search-softmax loss is found to be superior with 4% improvements with CASIA-WebFace-R and 1% improvements with MS-Celeb-1M-v1c-R at both the identification and verification. Based on these experiments, Search-Softmax loss can perform well, especially with a low false positive rate and it shows a strong generalization ability for face recognition.
Conclusion
In this paper, it is discussed that in order to enhance feature discrimination for face recognition, it is key to know how to reduce the softmax probability. To achieve this goal, unified formulation for the margin-based softmax losses is designed. Two search methods have been developed using a random and a reward-guided loss function and they were validated to be effective over six other methods using nine different test data sets. While these developed methods were generally more effective in increasing accuracy versus previous methods, there is very little difference between the two. It can be seen that Search-Softmax performs slightly better than Random-Softmax most of the time.
Critiques
- Thorough experimentation and comparison of results to state-of-the-art provided a convincing argument.
- Datasets used did require some preprocessing, which may have improved the results beyond what the method otherwise would.
- AM-LFS was created by the authors for experimentation (the code was not made public) so the comparison may not be accurate.
- The test data set they used to test Search-Softmax and Random-Softmax are simple and they saturate in other methods. So the results of their methods didn’t show many advantages since they produce very similar results. A more complicated data set needs to be tested to prove the method's reliability.
- There is another paper Large-Margin Softmax Loss for Convolutional Neural Networks[1] that provides a more detailed explanation about how to reduce margin-based softmax loss.
- It is questionable when it comes to the accuracy of testing sets, as they only used the clean version of CASIA-WebFace and MS-Celeb-1M-vlc for training instead of these two training sets with noisy labels.
- In a similar paper, written by Tae-Hyun Oh et al., they also discuss an optimal loss function for face recognition. However, since in the other paper, they were doing face recognition from voice audio, the loss function used was slightly different than the ones discussed in this paper.
- This model has many applications such as identifying disguised prisoners for police. But we need to do a good data preprocessing otherwise we might not get a good predicted result. But authors did not mention about the data preprocessing which is a key part of this model.
- It will be better if we can know what kind of noises was removed in the clean version. Also, simply removing the overlapping data is wasteful. It would be better to just put them into one of the train and test samples.
- This paper indicate that the new searching method and loss function have induced more effective face recognition result than other six methods. But there is no mention of the increase or decrease in computational efficiency since only very little difference exist between those methods and the real time evaluation is often required at the face recognition application level.
References
[1] X. Wang, S. Wang, C. Chi, S. Zhang and T. Mei, "Loss Function Search for Face Recognition", in International Conference on Machine Learning, 2020, pp. 1-10.
[2] Li, C., Yuan, X., Lin, C., Guo, M., Wu, W., Yan, J., and Ouyang, W. Am-lfs: Automl for loss function search. In Proceedings of the IEEE International Conference on Computer Vision, pp. 8410–8419, 2019. 2020].
[3] S. L. AI, “Reinforcement Learning algorithms - an intuitive overview,” Medium, 18-Feb-2019. [Online]. Available: https://medium.com/@SmartLabAI/reinforcement-learning-algorithms-an-intuitive-overview-904e2dff5bbc. [Accessed: 25-Nov-2020].
[4] “Reinforcement learning,” Wikipedia, 17-Nov-2020. [Online]. Available: https://en.wikipedia.org/wiki/Reinforcement_learning. [Accessed: 24-Nov-2020].
[5] B. Osiński, “What is reinforcement learning? The complete guide,” deepsense.ai, 23-Jul-2020. [Online]. Available: https://deepsense.ai/what-is-reinforcement-learning-the-complete-guide/. [Accessed: 25-Nov-2020].