Learning to Teach
Introduction
This paper proposed the "learning to teach" (L2T) framework with two intelligent agents: a student model/agent, corresponding to the learner in traditional machine learning algorithms, and a teacher model/agent, determining the appropriate data, loss function, and hypothesis space to facilitate the learning of the student model.
In modern human society, the role of teaching is heavily implicated in our education system; the goal is to equip students with the necessary knowledge and skills in an efficient manner. This is the fundamental student and teacher framework on which education stands. However, in the field of artificial intelligence (AI) and specifically machine learning, researchers have focused most of their efforts on the student (ie. designing various optimization algorithms to enhance the learning ability of intelligent agents). The paper argues that a formal study on the role of ‘teaching’ in AI is required. Analogous to teaching in human society, the teaching framework can: select training data that corresponds to the appropriate teaching materials (e.g. textbooks selected for the right difficulty), design loss functions that corresponds to targeted examinations, and define the hypothesis space that corresponds to imparting the proper methodologies. Furthermore, an optimization framework (instead of heuristics) should be used to update the teaching skills based on the feedback from students, so as to achieve teacher-student co-evolution.
Thus, the training phase of L2T would have several episodes of interactions between the teacher and the student model. Based on the state information in each step, the teacher model would update the teaching actions so that the student model could perform better on the Machine Learning problem. The student model would then provide reward signals back to the teacher model. These reward signals are used by the teacher model as part of the Reinforcement Learning process to update its parameters. This process is end-to-end trainable and the authors are convinced that once converged, the teacher model could be applied to new learning scenarios and even new students, without extra efforts on re-training.
To demonstrate the practical value of the proposed approach, the training data scheduling problem is chosen as an example. The authors show that by using the proposed method to adaptively select the most suitable training data, they can significantly improve the accuracy and convergence speed of various neural networks including multi-layer perceptron (MLP), convolutional neural networks (CNNs) and recurrent neural networks (RNNs), for different applications including image classification and text understanding.
Related Work
The L2T framework connects with two emerging trends in machine learning. The first is the movement from simple to advanced learning. This includes meta-learning (Schmidhuber, 1987; Thrun & Pratt, 2012) which explores automatic learning by transferring learned knowledge from meta tasks [1]. This approach has been applied to few-shot learning scenarios and in designing general optimizers and neural network architectures. (Hochreiter et al., 2001; Andrychowicz et al., 2016; Li & Malik, 2016; Zoph & Le, 2017)
The second is the teaching which can be classified into machine-teaching (Zhu, 2015) [2] and hardness based methods. The former seeks to construct a minimal training set for the student to learn a target model (ie. an oracle). The latter assumes an order of data from easy instances to hard ones, hardness being determined in different ways. In curriculum learning (CL) (Bengio et al, 2009; Spitkovsky et al. 2010; Tsvetkov et al, 2016) [3] measures hardness through heuristics of the data while self-paced learning (SPL) (Kumar et al., 2010; Lee & Grauman, 2011; Jiang et al., 2014; Supancic & Ramanan, 2013) [4] measures hardness by loss on data.
The limitations of these works boil down to a lack of formally defined teaching problem as well as the reliance on heuristics and fixed rules for teaching which hinders generalization of the teaching task.
Learning to Teach
To introduce the problem and framework, without loss of generality, consider the setting of supervised learning.
In supervised learning, each sample [math]\displaystyle{ x }[/math] is from a fixed but unknown distribution [math]\displaystyle{ P(x) }[/math], and the corresponding label [math]\displaystyle{ y }[/math] is from a fixed but unknown distribution [math]\displaystyle{ P(y|x) }[/math]. The goal is to find a function [math]\displaystyle{ f_\omega(x) }[/math] with parameter vector [math]\displaystyle{ \omega }[/math] that minimizes the gap between the predicted label and the actual label.
\usepackage{amssymb}
Problem Definition
The student model, denoted μ(), takes the set of training data [math]\displaystyle{ D }[/math], the function class [math]\displaystyle{ Ω }[/math], and loss function [math]\displaystyle{ L }[/math] as input to output a function, [math]\displaystyle{ f(ω) }[/math], with parameter [math]\displaystyle{ ω^* }[/math] which minimizes risk [math]\displaystyle{ R(ω) }[/math] as in:
\begin{align*} ω^* = arg min_{w \in \Omega} \sum_{x,y \in D} L(y, f_ω(x)) =: \mu (D, L, \Omega) \end{align*}
The teaching model, denoted φ, tries to provide [math]\displaystyle{ D }[/math], [math]\displaystyle{ L }[/math], and [math]\displaystyle{ Ω }[/math] (or any combination, denoted [math]\displaystyle{ A }[/math]) to the student model such that the student model either achieves lower risk R(ω) or progresses as fast as possible.
- Training Data: Outputting a good training set [math]\displaystyle{ D }[/math], analogous to human teachers providing students with proper learning materials such as textbooks.
- Loss Function: Designing a good loss function [math]\displaystyle{ L }[/math] , analogous to providing useful assessment criteria for students.
- Hypothesis Space: Defining a good function class [math]\displaystyle{ Ω }[/math] which the student model can select from. This is analogous to human teachers providing appropriate context, eg. middle school students taught math with basic algebra while undergraduate students are taught with calculus. Different Ω leads to different errors and optimization problem (Mohri et al., 2012).
Framework
The training phase consists of the teacher providing the student with the subset [math]\displaystyle{ A_{train} }[/math] of [math]\displaystyle{ A }[/math] and then taking feedback to improve its own parameters. The L2T process is outlined in figure below:
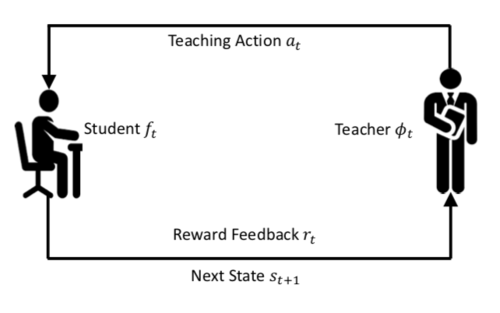
- [math]\displaystyle{ s_t ∈ S }[/math] represents information available to the teacher model at time [math]\displaystyle{ t }[/math]. [math]\displaystyle{ s_t }[/math] is typically constructed from the current student model [math]\displaystyle{ f_{t−1} }[/math] and the past teaching history of the teacher model.
- [math]\displaystyle{ a_t ∈ A }[/math] represents action taken the teacher model at time [math]\displaystyle{ t }[/math]. Can be any combination of teaching tasks involving the training data, loss function, and hypothesis space.
- [math]\displaystyle{ φ_θ : S → A }[/math] is policy used by the teacher model to generate its action [math]\displaystyle{ φ_θ(s_t) = a_t }[/math]
- Student model takes [math]\displaystyle{ a_t }[/math] as input and outputs function [math]\displaystyle{ f_t }[/math], by using the conventional ML techniques.
Once the training process converges, the teacher model may be utilized to teach a different subset of [math]\displaystyle{ A }[/math] or teach a different student model.
Application
There are different approaches to training the teacher model, this paper will apply reinforcement learning with [math]\displaystyle{ φ_θ }[/math] being the policy that interacts with [math]\displaystyle{ S }[/math], the environment. The paper applies data teaching to train a deep neural network student, [math]\displaystyle{ f }[/math], for several classification tasks. Thus the student feedback measure will be classification accuracy. Its learning rule will be mini-batch stochastic gradient descent, where batches of data will arrive sequentially in random order. The teacher model is responsible for providing the training data, which in this case means it must determine which instances (subset) of the mini-batch of data will be fed to the student.
The optimizer for training the teacher model is maximum expected reward:
\begin{align} J(θ) = E_{φ_θ(a|s)}[R(s,a)] \end{align}
Which is non-differentiable w.r.t. [math]\displaystyle{ θ }[/math], thus a likelihood ratio policy gradient algorithm is used to optimize [math]\displaystyle{ J(θ) }[/math] (Williams, 1992) [4]
Experiments
The L2T framework is tested on the following student models: multi-layer perceptron (MLP), ResNet (CNN), and Long-Short-Term-Memory network (RNN).
The student tasks are Image classification for MNIST, for CIFAR-10, and sentiment classification for IMDB movie review dataset.
The strategy will be benchmarked against the following teaching strategies:
- NoTeach: Outputting a good training set D, analogous to human teachers providing students with proper learning materials such as textbooks
- Self-Paced Learning (SPL): Teaching by hardness of data, defined as the loss. This strategy begins by filtering out data with larger loss value to train the student with "easy" data and gradually increases the hardness.
- L2T: The Learning to Teach framework.
- RandTeach: Randomly filter data in each epoch according to the logged ratio of filtered data instances per epoch (as opposed to deliberate and dynamic filtering by L2T).
Training a New Student
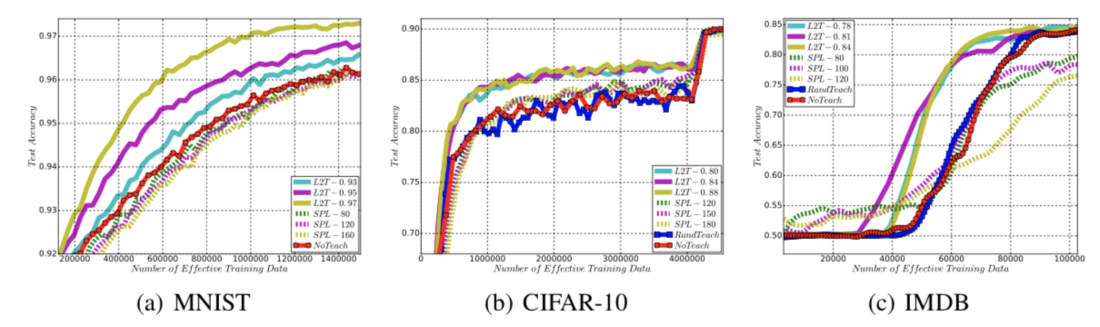
In the first set of experiments, the datasets or divided into two folds. The first folder is used to train the teacher; This is done by having the teacher train a student network on that half of the data, with a certain portion being used for computing rewards. After training, the teacher parameters are fixed, and used to train a new student network (with the same structure) on the second half of the dataset. When teaching a new student with the same model architecture, we observe that L2T achieves significantly faster convergence than other strategies across all tasks, especially compared to the NoTeach and RandTeach methods:
Filtration Number
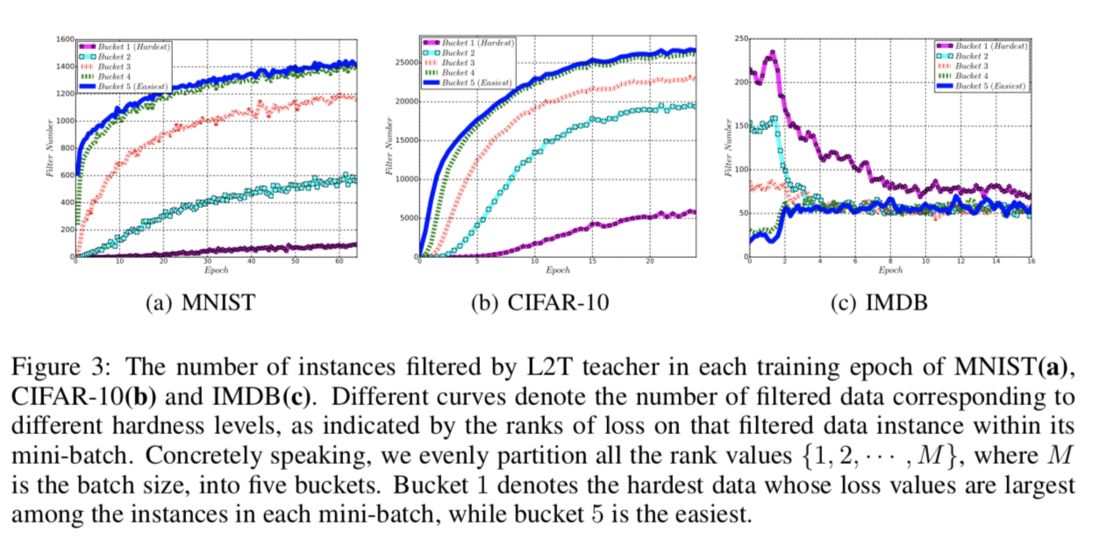
When investigating the details of filtered data instances per epoch, for the two image classification tasks, the L2T teacher filters an increasing amount of data as training goes on. The authors' intuition for the two image classification tasks is that the student model can learn from harder instances of data from the beginning, and thus the teacher can filter redundant data. In contrast, for training while for the natural language task, the student model must first learn from easy data instances.
Teaching New Student with Different Model Architecture
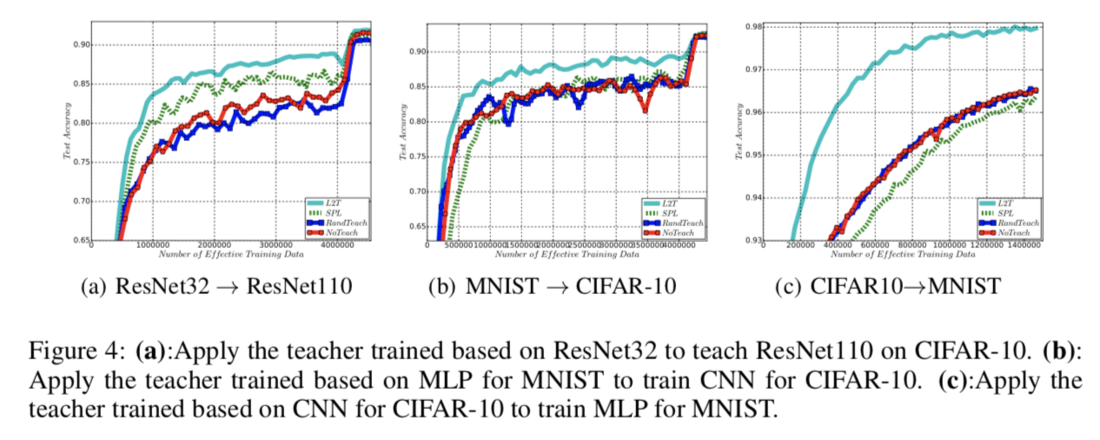
In this part, first a teacher model is trained by interacting with a student model. Then using the teacher model, another student model which has a different model architecture is taught. The results of Applying the teacher trained on ResNet32 to teach other architectures is shown below. The L2T algorithm can be seen to obtain higher accuracies earlier than the SPL, RandTeach, or NoTeach algorithms.
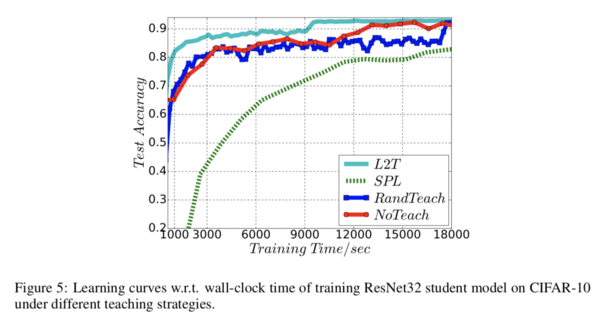
Training Time Analysis
The learning curves demonstrate the efficiency in accuracy achieved by the L2T over the other strategies. This is especially evident during the earlier training stages.
Accuracy Improvement
When comparing training accuracy on the IMDB sentiment classification task, L2T improves on teaching policy over NoTeach and SPL.

Future Work
There is some useful future work that can be extended from this work:
1) Recent advances in multi-agent reinforcement learning could be tried on the Reinforcement Learning problem formulation of this paper.
2) Some human in the loop architectures like CHAT and HAT (https://www.ijcai.org/proceedings/2017/0422.pdf) should give better results for the same framework.
3) It would be interesting to try out the framework suggested in this paper (L2T) in Imperfect information and partially observable settings.
Critique
While the conceptual framework of L2T is sound, the paper only experimentally demonstrates efficacy for data teaching which would seem to be the simplest to implement. The feasibility and effectiveness of teaching the loss function and hypothesis space are not explored in a real-world scenario. Furthermore, the experimental results for data teaching suggest that the speed of convergence is the main improvement over other teaching strategies whereas the difference in accuracy less remarkable. The paper also assesses accuracy only by comparing L2T with NoTeach and SPL on the IMDB classification task, the improvement (or lack thereof) on the other classification tasks and teaching strategies is omitted. Again, this distinction is not possible to assess in loss function or hypothesis space teaching within the scope of this paper.