Learning to Teach: Difference between revisions
No edit summary |
No edit summary |
||
| (63 intermediate revisions by 22 users not shown) | |||
| Line 1: | Line 1: | ||
This is a summary of the paper titled: "Learning to Teach", authored by Yang Fan, Fei Tian, Tao Qin, Xiang-Yang Li, and Tie-Yan Liu. Available online at URL https://arxiv.org/abs/1805.03643 | |||
=Introduction= | =Introduction= | ||
This paper proposed the "learning to teach" (L2T) framework with two intelligent agents: a student model/agent, corresponding to the learner in traditional machine learning algorithms, and a teacher model/agent, determining the appropriate data, loss function, and hypothesis space to facilitate the learning of the student model. | This paper proposed the "learning to teach" (L2T) framework with two intelligent agents: a student model/agent, corresponding to the learner in traditional machine learning algorithms, and a teacher model/agent, determining the appropriate data, loss function, and hypothesis space to facilitate the learning of the student model. | ||
In modern human society, the role of teaching is heavily implicated in our education system; the goal is to equip students with the necessary knowledge and skills in an efficient manner. This is the fundamental ''student'' and ''teacher'' framework on which education stands. However, in the field of artificial intelligence (AI) and specifically machine learning, researchers have focused most of their efforts on the ''student'' (ie. designing various optimization algorithms to enhance the learning ability of intelligent agents). The paper argues that a formal study on the role of ‘teaching’ in AI is required. Analogous to teaching in human society, the teaching framework can: select training data that corresponds to the appropriate teaching materials (e.g. textbooks selected for the right difficulty), design loss functions that correspond to targeted examinations and define the hypothesis space that corresponds to imparting the proper methodologies. Furthermore, an optimization framework (instead of heuristics) should be used to update the teaching skills based on the feedback from students, so as to achieve teacher-student co-evolution. | |||
Thus, the training phase of L2T would have several episodes of interactions between the teacher and the student model. Based on the state information in each step, the teacher model would update the teaching actions so that the student model could perform better on the Machine Learning problem. The student model would then provide reward signals back to the teacher model. These reward signals are used by the teacher model as part of the Reinforcement Learning process to update its parameters. In this paper policy gradient algorithm is incorporated. This process is end-to-end trainable and the authors are convinced that once converged, the teacher model could be applied to new learning scenarios and even new students, without extra efforts on re-training. | |||
To demonstrate the practical value of the proposed approach, the '''training data scheduling''' problem is chosen as an example. The authors show that by using the proposed method to adaptively select the most | |||
suitable training data, they can significantly improve the accuracy and convergence speed of various neural networks including multi-layer perceptron (MLP), convolutional neural networks (CNNs) | |||
and recurrent neural networks (RNNs), for different applications including image classification and text understanding. | |||
Furthermore , the teacher model obtained by the paper from one task can be smoothly transferred to other tasks. As an example, the teacher model trained on MNIST with the MLP learner, one can achieve a satisfactory performance on CIFAR-10 only using roughly half | |||
of the training data to train a ResNet model as the student. | |||
=Related Work= | =Related Work= | ||
The L2T framework connects with two trends in machine learning. | The L2T framework connects with two emerging trends in machine learning. The first is the movement from simple to advanced learning. This includes meta-learning (Schmidhuber, 1987; Thrun & Pratt, 2012) which explores automatic learning by transferring learned knowledge from meta tasks [1]. This approach has been applied to few-shot learning scenarios and in designing general optimizers and neural network architectures. (Hochreiter et al., 2001; Andrychowicz et al., 2016; Li & Malik, 2016; Zoph & Le, 2017) | ||
The second is the teaching, which can be classified into either machine-teaching (Zhu, 2015) [2] or hardness based methods. The former seeks to construct a minimal training set for the student to learn a target model (ie. an oracle). The latter assumes an order of data from easy instances to hard ones, hardness being determined in different ways, is beneficial to the learning process. In curriculum learning (CL) (Bengio et al, 2009; Spitkovsky et al. 2010; Tsvetkov et al, 2016) [3] measures hardness through heuristics based understanding of the data while self-paced learning (SPL) (Kumar et al., 2010; Lee & Grauman, 2011; Jiang et al., 2014; Supancic & Ramanan, 2013) [4] measures hardness by loss on data. Another teaching method called 'pedagogical teaching' with applications in inverse reinforcement learning is quite close, in setup, to the method being proposed in this paper. The similarity can be observed in the way the teacher adjusts its behaviour to facilitate student learning and in the way the teacher communicates with the student. | |||
The limitations of these works include the lack of a formal definition of the teaching problem whereas a learning problem has been a formal mathematical definition. This makes it difficult to differentiate between teaching and learning problems. Other limitations are the reliance on heuristics and fixed rules, which hinders generalization of the teaching task. | |||
=Learning to Teach= | |||
To introduce the problem and framework, without loss of generality, consider the setting of supervised learning. | |||
In supervised learning, each sample <math>x</math> is from a fixed but unknown distribution <math>P(x)</math>, and the corresponding label <math> y </math> is from a fixed but unknown distribution <math>P(y|x) </math>. The goal is to find a function <math>f_\omega(x)</math> with parameter vector <math>\omega</math> that minimizes the gap between the predicted label and the actual label. | |||
==Problem Definition== | |||
In supervised learning, the goal is to choose a function <math display="inline">f_w(x)</math> with <math display="inline">w</math> as the parameter vector to predict the supervisor's label as good as possible. The goodness of a function <math display="inline">f_w</math> is evaluated by the risk function: | |||
\begin{align*}R(w) = \int M(y, f_w(x))dP(x,y)\end{align*} | |||
where <math display="inline">\mathcal{M}(,)</math> is the metric which evaluates the gap between the label and the prediction. | |||
The student model, denoted μ(), takes the set of training data <math> D </math>, the function class <math> Ω </math>, and loss function <math> L </math> as input to output a function, <math> f(ω) </math>, with parameter <math>ω^*</math> which minimizes risk <math>R(ω)</math> as in: | |||
\begin{align*} | |||
ω^* = arg min_{w \in \Omega} \sum_{x,y \in D} L(y, f_ω(x)) =: \mu (D, L, \Omega) | |||
\end{align*} | |||
The teaching model, denoted φ, tries to provide <math> D </math>, <math> L </math>, and <math> Ω </math> (or any combination, denoted <math> A </math>) to the student model such that the student model either achieves lower risk R(ω) or progresses as fast as possible. | |||
In contrast to traditional machine learning, which is only concerned with the student model in the | |||
learning to teach framework, the problem in the paper is also concerned with a teacher model, which tries to provide | |||
appropriate inputs to the student model so that it can achieve low risk functional as efficiently | |||
as possible. | |||
::'''Training Data''': Outputting a good training set <math> D \in \mathcal{D} </math>, where <math>\mathcal{D}</math> is the Borel set on the input space and label space. This is analogous to human teachers providing students with proper learning materials such as textbooks. | |||
::'''Loss Function''': Designing a good loss function <math> L \in \mathcal{L} </math>, where <math>\mathcal{L}</math> is the set of all possible loss functions. This is analogous to providing useful assessment criteria for students. | |||
::'''Hypothesis Space''': Defining a good function class <math> Ω \in \mathcal{W}</math>, where <math>\mathcal{W}</math> is the set of possible hypothesis spaces, which the student model can select from. This is analogous to human teachers providing appropriate context, eg. middle school students taught math with basic algebra while undergraduate students are taught with calculus. Different Ω leads to different errors and optimization problem (Mohri et al., 2012). | |||
==Framework== | |||
The training phase consists of the teacher providing the student with the subset <math> A_{train} </math> of <math> A </math> and then taking feedback to improve its own parameters.After the convergence of the training process, | |||
the teacher model can be used to teach either | |||
new student models, or the same student | |||
models in new learning scenarios such as another | |||
subset <math> A_{test} </math>is provided. Such a generalization is feasible as long as the state representations | |||
S are the same across different student | |||
models and different scenarios. The L2T process is outlined in the figure below: | |||
[[File: L2T_process.png | 500px|center]] | |||
* <math> s_t ∈ S </math> represents information available to the teacher model at time <math> t </math>. <math> s_t </math> is typically constructed from the current student model <math> f_{t−1} </math> and the past teaching history of the teacher model. <math> S </math> represents the set of states. | |||
* <math> a_t ∈ A </math> represents action taken the teacher model at time <math> t </math>, given state <math>s_t</math>. <math> A </math> represents the set of actions, where the action(s) can be any combination of teaching tasks involving the training data, loss function, and hypothesis space. | |||
* <math> φ_θ : S → A </math> is policy used by the teacher model to generate its action <math> φ_θ(s_t) = a_t </math> | |||
* Student model takes <math> a_t </math> as input and outputs function <math> f_t </math>, by using the conventional ML techniques. | |||
Mathematically, taking data teaching as an example where <math>L</math> <math>/Omega</math> as fixed, the objective of the teacher in the L2T framework is | |||
<center> <math>\max\limits_{\theta}{\sum\limits_{t}{r_t}} = \max\limits_{\theta}{\sum\limits_{t}{r(f_t)}} = \max\limits_{\theta}{\sum\limits_{t}{r(\mu(\phi_{\theta}(s_t), L, \Omega))}}</math> </center> | |||
Once the training process converges, the teacher model may be utilized to teach a different subset of <math> A </math> or teach a different student model. | |||
=Application= | |||
There are different approaches to training the teacher model, this paper will apply reinforcement learning with <math> φ_θ </math> being the ''policy'' that interacts with <math> S </math>, the ''environment''. The paper applies data teaching to train a deep neural network student, <math> f </math>, for several classification tasks. Thus the student feedback measure will be classification accuracy. Its learning rule will be mini-batch stochastic gradient descent, where batches of data will arrive sequentially in random order. The teacher model is responsible for providing the training data, which in this case means it must determine which instances (subset) of the mini-batch of data will be fed to the student. In order to reach the convergence faster, the reward was set to relate to the speed the student model learns. | |||
The authors also designed a state feature vector <math> g(s) </math> in order to efficiently represent the current states which include arrived training data and the student model. Within the State Features, there are three categories including Data features, student model features and the combination of both data and learner model. This state feature will be computed when each mini-batch of data arrives. | |||
Data features contain information for data instance, such as its label category, (for texts) the length of sentence, linguistic features for text segments (Tsvetkov et al., 2016), or (for images) gradients histogram features (Dalal & Triggs, 2005). | |||
Student model features include the signals reflecting how well current neural network is trained. The authors collect several simple features, such as passed mini-batch number (i.e., iteration), the average historical training loss and historical validation accuracy. | |||
Some additional features are collected to represent the combination of both data and learner model. By using these features, the authors aim to represent how important the arrived training data is for current leaner. The authors mainly use three parts of such signals in our classification tasks: 1) the predicted probabilities of each class; 2) the loss value on that data, which appears frequently in self-paced learning (Kumar et al., 2010; Jiang et al., 2014a; Sachan & Xing, 2016); 3) the margin value. | |||
The optimizer for training the teacher model is the maximum expected reward: | |||
\begin{align} | |||
J(θ) = E_{φ_θ(a|s)}[R(s,a)] | |||
\end{align} | |||
Which is non-differentiable w.r.t. <math> θ </math>, thus a likelihood ratio policy gradient algorithm is used to optimize <math> J(θ) </math> (Williams, 1992) [4]. The estimation is based on the gradient <math>\nabla_{\theta} = \sum_{t=1}^{T}E_{\phi_{\theta}}(a_t|s_t)[\nabla_{\theta}log(\phi_{\theta}(a_t|s_t))R(s_t, a_t)]</math>, which is empirically estimated as <math>\sum_{t=1}^{T} \nabla_{\theta}log(\phi_{\theta}(a_t|s_t))v_t</math>. <math>v_t</math> is defined as the sampled estimation of reward <math>R(s_t, a_t)</math> from one execution of the policy. Given that the reward is just the terminal reward, we have <math>\nabla_{\theta} = \sum_{t=1}^{T} \nabla_{\theta}log(\phi_{\theta}(a_t|s_t))r_T</math> | |||
==Experiments== | |||
The L2T framework is tested on the following student models: multi-layer perceptron (MLP), ResNet (CNN), and Long-Short-Term-Memory network (RNN). | |||
The student tasks are Image classification for MNIST, for CIFAR-10, and sentiment classification for IMDB movie review dataset. | |||
The strategy will be benchmarked against the following teaching strategies: | |||
::'''NoTeach''': NoTeach removes the entire Teacher-Student paradigm and reverts back to the classical machine learning paradigm. In the context of data teaching, we consider the architecture fixed, and feed data in a pre-determined way. One would pre-define batch-size and cross-validation procedures as needed. | |||
::'''Self-Paced Learning (SPL)''': Teaching by ''hardness'' of data, defined as the loss. This strategy begins by filtering out data with larger loss value to train the student with "easy" data and gradually increases the hardness. Mathematically speaking, those training data <math>d </math> satisfying loss value <math>l(d) > \eta </math> will be filtered out, where the threshold <math> \eta </math> grows from smaller to larger during the training process. To improve the robustness of SPL, following the widely used trick in common SPL implementation (Jiang et al., 2014b), the authors filter training data using its loss rank in one mini-batch rather than the absolute loss value: they filter data instances with top <math>K </math>largest training loss values within a <math>M</math>-sized mini-batch, where <math>K</math> linearly drops from <math>M − 1 </math>to 0 during training. | |||
::'''L2T''': The Learning to Teach framework. | |||
::'''RandTeach''': Randomly filter data in each epoch according to the logged ratio of filtered data instances per epoch (as opposed to deliberate and dynamic filtering by L2T). | |||
For all teaching strategies, they make sure that the base neural network model will not be updated until <math>M </math> un-trained, yet selected data instances are accumulated. That is to guarantee that the convergence speed is only determined by the quality of taught data, not by different model updating frequencies. The model is implemented with Theano and run on one NVIDIA Tesla K40 GPU for each training/testing process. | |||
===Training a New Student=== | |||
In the first set of experiments, the datasets or divided into two folds. The first folder is used to train the teacher; This is done by having the teacher train a student network on that half of the data, with a certain portion being used for computing rewards. After training, the teacher parameters are fixed and used to train a new student network (with the same structure) on the second half of the dataset. When teaching a new student with the same model architecture, we observe that L2T achieves significantly faster convergence than other strategies across all tasks, especially compared to the NoTeach and RandTeach methods: | |||
[[File: L2T_speed.png | 1100px|center]] | |||
===Filtration Number=== | |||
When investigating the details of filtered data instances per epoch, for the two image classification tasks, the L2T teacher filters an increasing amount of data as training goes on. The authors' intuition for the two image classification tasks is that the student model can learn from harder instances of data from the beginning, and thus the teacher can filter redundant data. In contrast, for training while for the natural language task, the student model must first learn from easy data instances. | |||
[[File: L2T_fig3.png | 1100px|center]] | |||
===Teaching New Student with Different Model Architecture=== | |||
In this part, first a teacher model is trained by interacting with a student model. Then using the teacher model, another student model | |||
which has a different model architecture is taught. | |||
The results of Applying the teacher trained on ResNet32 to teach other architectures is shown below. The L2T algorithm can be seen to obtain higher accuracies earlier than the SPL, RandTeach, or NoTeach algorithms. | |||
[[File: L2T_fig4.png | 1100px|center]] | |||
===Training Time Analysis=== | |||
The learning curves demonstrate the efficiency in accuracy achieved by the L2T over the other strategies. This is especially evident during the earlier training stages. | |||
[[File: L2T_fig5.png | 600px|center]] | |||
===Accuracy Improvement=== | |||
When comparing training accuracy on the IMDB sentiment classification task, L2T improves on teaching policy over NoTeach and SPL. | |||
[[File: L2T_t1.png | 500px|center]] | |||
Table 1 shows that we boost the convergence speed, while the teacher model improves final accuracy. The student model is the LSTM network trained on IMDB. Prior to teaching the student model, we train the teacher model on half of the training data, and define the terminal reward as the set accuracy after the teacher model trains the student for 15 epochs. Then the teacher model is applied to train the student model on the full dataset till its convergence. The state features are kept the same as those in previous experiments. We can see that L2T achieves better classification accuracy for training LSTM network, surpassing the SPL baseline by more than 0.6 point (with p value < 0.001). | |||
=Future Work= | |||
There is some useful future work that can be extended from this work: | |||
1) Recent advances in multi-agent reinforcement learning could be tried on the Reinforcement Learning problem formulation of this paper. | |||
2) Some human in the loop architectures like CHAT and HAT (https://www.ijcai.org/proceedings/2017/0422.pdf) should give better results for the same framework. | |||
3) It would be interesting to try out the framework suggested in this paper (L2T) in Imperfect information and partially observable settings. | |||
4) As they have focused on data teaching exploring loss function teaching would be interesting. | |||
=Critique= | |||
While the conceptual framework of L2T is sound, the paper only experimentally demonstrates efficacy for ''data teaching'' which would seem to be the simplest to implement. The feasibility and effectiveness of teaching the loss function and hypothesis space are not explored in a real-world scenario. Also, this paper does not provide enough mathematical foundation to prove that this model can be generalized to other datasets and other general problems. The method presented here where the teacher model filters data does not seem to provide enough action space for the teacher model. Furthermore, the experimental results for data teaching suggest that the speed of convergence is the main improvement over other teaching strategies whereas the difference in accuracy less remarkable. The paper also assesses accuracy only by comparing L2T with NoTeach and SPL on the IMDB classification task, the improvement (or lack thereof) on the other classification tasks and teaching strategies is omitted. Again, this distinction is not possible to assess in loss function or hypothesis space teaching within the scope of this paper. They could have included larger datasets such as ImageNet and CIFAR100 in their experiments which would have provided some more insight. | |||
Also, teaching should not be limited to data, loss function and hypothesis space. In a human teacher-student model, the teaching contents are concepts and logical rules, similar to weights of hidden layers in neural networks. How to transfer such knowledge is interesting to investigate. | |||
The idea of having a generalizable teacher model to enhance student learning is admirable. In fact, the L2T framework is similar to the reinforcement learning actor-critic model, which is known to be effective. In general, one expects an effective teacher model would facilitate transfer learning and can significantly reduce student model training time. However, the T2L framework seems to fall short of that goal. Consider the CIFAR10 training scenario, the L2T model achieve 85% accuracy after 2 million training data, which is only about 3% more accuracy than a no-teacher model. Perhaps in the future, the L2T framework can improve and produce better performance. | |||
Latest revision as of 18:40, 16 December 2018
This is a summary of the paper titled: "Learning to Teach", authored by Yang Fan, Fei Tian, Tao Qin, Xiang-Yang Li, and Tie-Yan Liu. Available online at URL https://arxiv.org/abs/1805.03643
Introduction
This paper proposed the "learning to teach" (L2T) framework with two intelligent agents: a student model/agent, corresponding to the learner in traditional machine learning algorithms, and a teacher model/agent, determining the appropriate data, loss function, and hypothesis space to facilitate the learning of the student model.
In modern human society, the role of teaching is heavily implicated in our education system; the goal is to equip students with the necessary knowledge and skills in an efficient manner. This is the fundamental student and teacher framework on which education stands. However, in the field of artificial intelligence (AI) and specifically machine learning, researchers have focused most of their efforts on the student (ie. designing various optimization algorithms to enhance the learning ability of intelligent agents). The paper argues that a formal study on the role of ‘teaching’ in AI is required. Analogous to teaching in human society, the teaching framework can: select training data that corresponds to the appropriate teaching materials (e.g. textbooks selected for the right difficulty), design loss functions that correspond to targeted examinations and define the hypothesis space that corresponds to imparting the proper methodologies. Furthermore, an optimization framework (instead of heuristics) should be used to update the teaching skills based on the feedback from students, so as to achieve teacher-student co-evolution.
Thus, the training phase of L2T would have several episodes of interactions between the teacher and the student model. Based on the state information in each step, the teacher model would update the teaching actions so that the student model could perform better on the Machine Learning problem. The student model would then provide reward signals back to the teacher model. These reward signals are used by the teacher model as part of the Reinforcement Learning process to update its parameters. In this paper policy gradient algorithm is incorporated. This process is end-to-end trainable and the authors are convinced that once converged, the teacher model could be applied to new learning scenarios and even new students, without extra efforts on re-training.
To demonstrate the practical value of the proposed approach, the training data scheduling problem is chosen as an example. The authors show that by using the proposed method to adaptively select the most suitable training data, they can significantly improve the accuracy and convergence speed of various neural networks including multi-layer perceptron (MLP), convolutional neural networks (CNNs) and recurrent neural networks (RNNs), for different applications including image classification and text understanding. Furthermore , the teacher model obtained by the paper from one task can be smoothly transferred to other tasks. As an example, the teacher model trained on MNIST with the MLP learner, one can achieve a satisfactory performance on CIFAR-10 only using roughly half of the training data to train a ResNet model as the student.
Related Work
The L2T framework connects with two emerging trends in machine learning. The first is the movement from simple to advanced learning. This includes meta-learning (Schmidhuber, 1987; Thrun & Pratt, 2012) which explores automatic learning by transferring learned knowledge from meta tasks [1]. This approach has been applied to few-shot learning scenarios and in designing general optimizers and neural network architectures. (Hochreiter et al., 2001; Andrychowicz et al., 2016; Li & Malik, 2016; Zoph & Le, 2017)
The second is the teaching, which can be classified into either machine-teaching (Zhu, 2015) [2] or hardness based methods. The former seeks to construct a minimal training set for the student to learn a target model (ie. an oracle). The latter assumes an order of data from easy instances to hard ones, hardness being determined in different ways, is beneficial to the learning process. In curriculum learning (CL) (Bengio et al, 2009; Spitkovsky et al. 2010; Tsvetkov et al, 2016) [3] measures hardness through heuristics based understanding of the data while self-paced learning (SPL) (Kumar et al., 2010; Lee & Grauman, 2011; Jiang et al., 2014; Supancic & Ramanan, 2013) [4] measures hardness by loss on data. Another teaching method called 'pedagogical teaching' with applications in inverse reinforcement learning is quite close, in setup, to the method being proposed in this paper. The similarity can be observed in the way the teacher adjusts its behaviour to facilitate student learning and in the way the teacher communicates with the student.
The limitations of these works include the lack of a formal definition of the teaching problem whereas a learning problem has been a formal mathematical definition. This makes it difficult to differentiate between teaching and learning problems. Other limitations are the reliance on heuristics and fixed rules, which hinders generalization of the teaching task.
Learning to Teach
To introduce the problem and framework, without loss of generality, consider the setting of supervised learning.
In supervised learning, each sample [math]\displaystyle{ x }[/math] is from a fixed but unknown distribution [math]\displaystyle{ P(x) }[/math], and the corresponding label [math]\displaystyle{ y }[/math] is from a fixed but unknown distribution [math]\displaystyle{ P(y|x) }[/math]. The goal is to find a function [math]\displaystyle{ f_\omega(x) }[/math] with parameter vector [math]\displaystyle{ \omega }[/math] that minimizes the gap between the predicted label and the actual label.
Problem Definition
In supervised learning, the goal is to choose a function [math]\displaystyle{ f_w(x) }[/math] with [math]\displaystyle{ w }[/math] as the parameter vector to predict the supervisor's label as good as possible. The goodness of a function [math]\displaystyle{ f_w }[/math] is evaluated by the risk function:
\begin{align*}R(w) = \int M(y, f_w(x))dP(x,y)\end{align*}
where [math]\displaystyle{ \mathcal{M}(,) }[/math] is the metric which evaluates the gap between the label and the prediction.
The student model, denoted μ(), takes the set of training data [math]\displaystyle{ D }[/math], the function class [math]\displaystyle{ Ω }[/math], and loss function [math]\displaystyle{ L }[/math] as input to output a function, [math]\displaystyle{ f(ω) }[/math], with parameter [math]\displaystyle{ ω^* }[/math] which minimizes risk [math]\displaystyle{ R(ω) }[/math] as in:
\begin{align*} ω^* = arg min_{w \in \Omega} \sum_{x,y \in D} L(y, f_ω(x)) =: \mu (D, L, \Omega) \end{align*}
The teaching model, denoted φ, tries to provide [math]\displaystyle{ D }[/math], [math]\displaystyle{ L }[/math], and [math]\displaystyle{ Ω }[/math] (or any combination, denoted [math]\displaystyle{ A }[/math]) to the student model such that the student model either achieves lower risk R(ω) or progresses as fast as possible. In contrast to traditional machine learning, which is only concerned with the student model in the learning to teach framework, the problem in the paper is also concerned with a teacher model, which tries to provide appropriate inputs to the student model so that it can achieve low risk functional as efficiently as possible.
- Training Data: Outputting a good training set [math]\displaystyle{ D \in \mathcal{D} }[/math], where [math]\displaystyle{ \mathcal{D} }[/math] is the Borel set on the input space and label space. This is analogous to human teachers providing students with proper learning materials such as textbooks.
- Loss Function: Designing a good loss function [math]\displaystyle{ L \in \mathcal{L} }[/math], where [math]\displaystyle{ \mathcal{L} }[/math] is the set of all possible loss functions. This is analogous to providing useful assessment criteria for students.
- Hypothesis Space: Defining a good function class [math]\displaystyle{ Ω \in \mathcal{W} }[/math], where [math]\displaystyle{ \mathcal{W} }[/math] is the set of possible hypothesis spaces, which the student model can select from. This is analogous to human teachers providing appropriate context, eg. middle school students taught math with basic algebra while undergraduate students are taught with calculus. Different Ω leads to different errors and optimization problem (Mohri et al., 2012).
Framework
The training phase consists of the teacher providing the student with the subset [math]\displaystyle{ A_{train} }[/math] of [math]\displaystyle{ A }[/math] and then taking feedback to improve its own parameters.After the convergence of the training process, the teacher model can be used to teach either new student models, or the same student models in new learning scenarios such as another subset [math]\displaystyle{ A_{test} }[/math]is provided. Such a generalization is feasible as long as the state representations S are the same across different student models and different scenarios. The L2T process is outlined in the figure below:
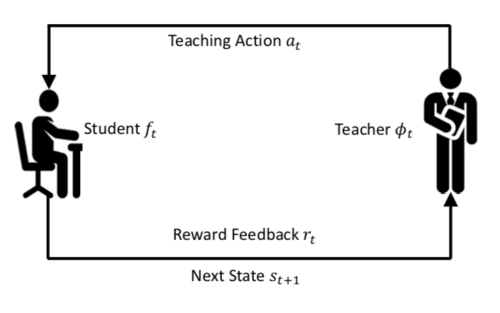
- [math]\displaystyle{ s_t ∈ S }[/math] represents information available to the teacher model at time [math]\displaystyle{ t }[/math]. [math]\displaystyle{ s_t }[/math] is typically constructed from the current student model [math]\displaystyle{ f_{t−1} }[/math] and the past teaching history of the teacher model. [math]\displaystyle{ S }[/math] represents the set of states.
- [math]\displaystyle{ a_t ∈ A }[/math] represents action taken the teacher model at time [math]\displaystyle{ t }[/math], given state [math]\displaystyle{ s_t }[/math]. [math]\displaystyle{ A }[/math] represents the set of actions, where the action(s) can be any combination of teaching tasks involving the training data, loss function, and hypothesis space.
- [math]\displaystyle{ φ_θ : S → A }[/math] is policy used by the teacher model to generate its action [math]\displaystyle{ φ_θ(s_t) = a_t }[/math]
- Student model takes [math]\displaystyle{ a_t }[/math] as input and outputs function [math]\displaystyle{ f_t }[/math], by using the conventional ML techniques.
Mathematically, taking data teaching as an example where [math]\displaystyle{ L }[/math] [math]\displaystyle{ /Omega }[/math] as fixed, the objective of the teacher in the L2T framework is
Once the training process converges, the teacher model may be utilized to teach a different subset of [math]\displaystyle{ A }[/math] or teach a different student model.
Application
There are different approaches to training the teacher model, this paper will apply reinforcement learning with [math]\displaystyle{ φ_θ }[/math] being the policy that interacts with [math]\displaystyle{ S }[/math], the environment. The paper applies data teaching to train a deep neural network student, [math]\displaystyle{ f }[/math], for several classification tasks. Thus the student feedback measure will be classification accuracy. Its learning rule will be mini-batch stochastic gradient descent, where batches of data will arrive sequentially in random order. The teacher model is responsible for providing the training data, which in this case means it must determine which instances (subset) of the mini-batch of data will be fed to the student. In order to reach the convergence faster, the reward was set to relate to the speed the student model learns.
The authors also designed a state feature vector [math]\displaystyle{ g(s) }[/math] in order to efficiently represent the current states which include arrived training data and the student model. Within the State Features, there are three categories including Data features, student model features and the combination of both data and learner model. This state feature will be computed when each mini-batch of data arrives.
Data features contain information for data instance, such as its label category, (for texts) the length of sentence, linguistic features for text segments (Tsvetkov et al., 2016), or (for images) gradients histogram features (Dalal & Triggs, 2005).
Student model features include the signals reflecting how well current neural network is trained. The authors collect several simple features, such as passed mini-batch number (i.e., iteration), the average historical training loss and historical validation accuracy.
Some additional features are collected to represent the combination of both data and learner model. By using these features, the authors aim to represent how important the arrived training data is for current leaner. The authors mainly use three parts of such signals in our classification tasks: 1) the predicted probabilities of each class; 2) the loss value on that data, which appears frequently in self-paced learning (Kumar et al., 2010; Jiang et al., 2014a; Sachan & Xing, 2016); 3) the margin value.
The optimizer for training the teacher model is the maximum expected reward:
\begin{align} J(θ) = E_{φ_θ(a|s)}[R(s,a)] \end{align}
Which is non-differentiable w.r.t. [math]\displaystyle{ θ }[/math], thus a likelihood ratio policy gradient algorithm is used to optimize [math]\displaystyle{ J(θ) }[/math] (Williams, 1992) [4]. The estimation is based on the gradient [math]\displaystyle{ \nabla_{\theta} = \sum_{t=1}^{T}E_{\phi_{\theta}}(a_t|s_t)[\nabla_{\theta}log(\phi_{\theta}(a_t|s_t))R(s_t, a_t)] }[/math], which is empirically estimated as [math]\displaystyle{ \sum_{t=1}^{T} \nabla_{\theta}log(\phi_{\theta}(a_t|s_t))v_t }[/math]. [math]\displaystyle{ v_t }[/math] is defined as the sampled estimation of reward [math]\displaystyle{ R(s_t, a_t) }[/math] from one execution of the policy. Given that the reward is just the terminal reward, we have [math]\displaystyle{ \nabla_{\theta} = \sum_{t=1}^{T} \nabla_{\theta}log(\phi_{\theta}(a_t|s_t))r_T }[/math]
Experiments
The L2T framework is tested on the following student models: multi-layer perceptron (MLP), ResNet (CNN), and Long-Short-Term-Memory network (RNN).
The student tasks are Image classification for MNIST, for CIFAR-10, and sentiment classification for IMDB movie review dataset.
The strategy will be benchmarked against the following teaching strategies:
- NoTeach: NoTeach removes the entire Teacher-Student paradigm and reverts back to the classical machine learning paradigm. In the context of data teaching, we consider the architecture fixed, and feed data in a pre-determined way. One would pre-define batch-size and cross-validation procedures as needed.
- Self-Paced Learning (SPL): Teaching by hardness of data, defined as the loss. This strategy begins by filtering out data with larger loss value to train the student with "easy" data and gradually increases the hardness. Mathematically speaking, those training data [math]\displaystyle{ d }[/math] satisfying loss value [math]\displaystyle{ l(d) \gt \eta }[/math] will be filtered out, where the threshold [math]\displaystyle{ \eta }[/math] grows from smaller to larger during the training process. To improve the robustness of SPL, following the widely used trick in common SPL implementation (Jiang et al., 2014b), the authors filter training data using its loss rank in one mini-batch rather than the absolute loss value: they filter data instances with top [math]\displaystyle{ K }[/math]largest training loss values within a [math]\displaystyle{ M }[/math]-sized mini-batch, where [math]\displaystyle{ K }[/math] linearly drops from [math]\displaystyle{ M − 1 }[/math]to 0 during training.
- L2T: The Learning to Teach framework.
- RandTeach: Randomly filter data in each epoch according to the logged ratio of filtered data instances per epoch (as opposed to deliberate and dynamic filtering by L2T).
For all teaching strategies, they make sure that the base neural network model will not be updated until [math]\displaystyle{ M }[/math] un-trained, yet selected data instances are accumulated. That is to guarantee that the convergence speed is only determined by the quality of taught data, not by different model updating frequencies. The model is implemented with Theano and run on one NVIDIA Tesla K40 GPU for each training/testing process.
Training a New Student
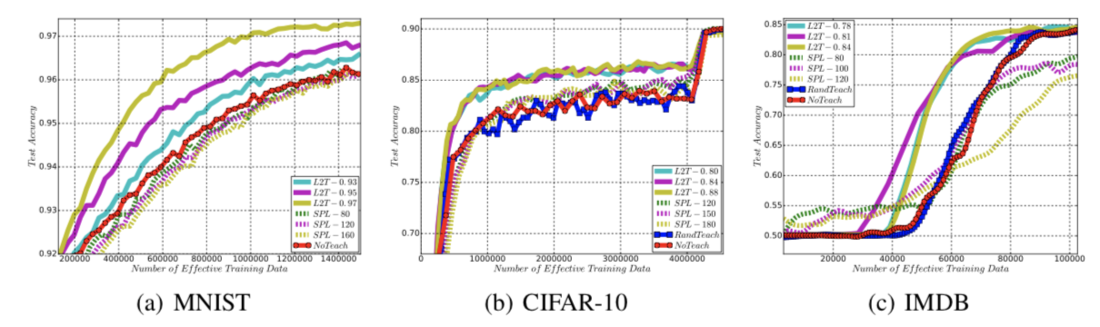
In the first set of experiments, the datasets or divided into two folds. The first folder is used to train the teacher; This is done by having the teacher train a student network on that half of the data, with a certain portion being used for computing rewards. After training, the teacher parameters are fixed and used to train a new student network (with the same structure) on the second half of the dataset. When teaching a new student with the same model architecture, we observe that L2T achieves significantly faster convergence than other strategies across all tasks, especially compared to the NoTeach and RandTeach methods:
Filtration Number
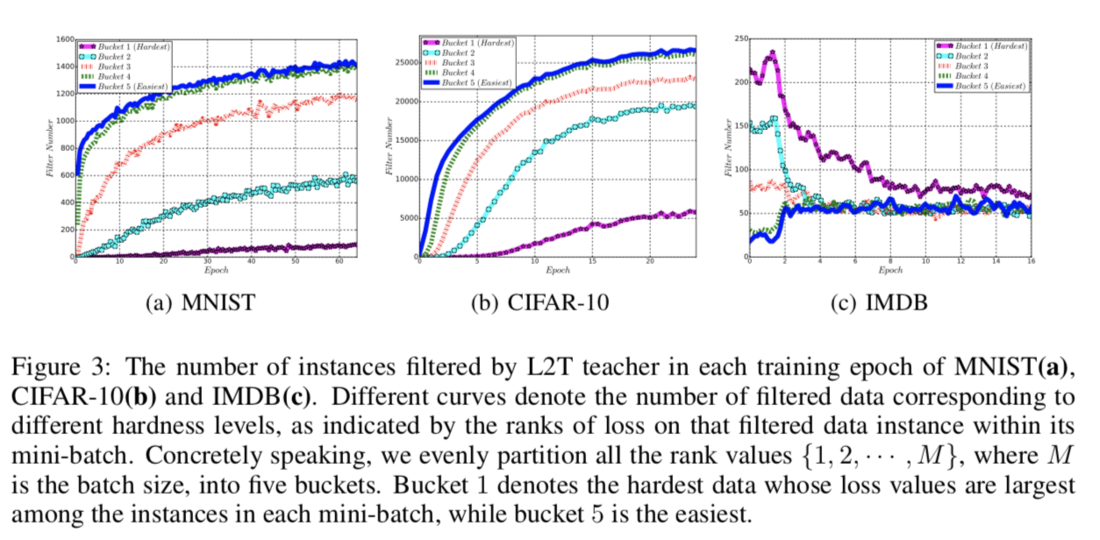
When investigating the details of filtered data instances per epoch, for the two image classification tasks, the L2T teacher filters an increasing amount of data as training goes on. The authors' intuition for the two image classification tasks is that the student model can learn from harder instances of data from the beginning, and thus the teacher can filter redundant data. In contrast, for training while for the natural language task, the student model must first learn from easy data instances.
Teaching New Student with Different Model Architecture
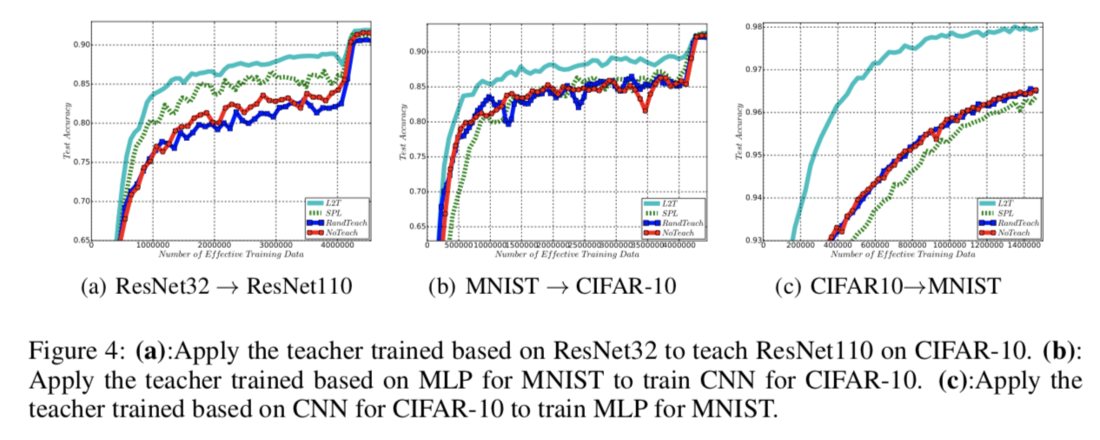
In this part, first a teacher model is trained by interacting with a student model. Then using the teacher model, another student model which has a different model architecture is taught. The results of Applying the teacher trained on ResNet32 to teach other architectures is shown below. The L2T algorithm can be seen to obtain higher accuracies earlier than the SPL, RandTeach, or NoTeach algorithms.
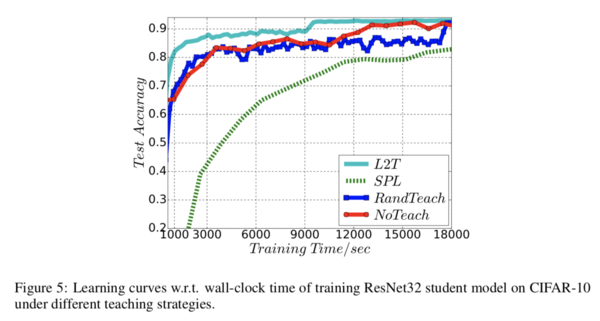
Training Time Analysis
The learning curves demonstrate the efficiency in accuracy achieved by the L2T over the other strategies. This is especially evident during the earlier training stages.
Accuracy Improvement
When comparing training accuracy on the IMDB sentiment classification task, L2T improves on teaching policy over NoTeach and SPL.

Table 1 shows that we boost the convergence speed, while the teacher model improves final accuracy. The student model is the LSTM network trained on IMDB. Prior to teaching the student model, we train the teacher model on half of the training data, and define the terminal reward as the set accuracy after the teacher model trains the student for 15 epochs. Then the teacher model is applied to train the student model on the full dataset till its convergence. The state features are kept the same as those in previous experiments. We can see that L2T achieves better classification accuracy for training LSTM network, surpassing the SPL baseline by more than 0.6 point (with p value < 0.001).
Future Work
There is some useful future work that can be extended from this work:
1) Recent advances in multi-agent reinforcement learning could be tried on the Reinforcement Learning problem formulation of this paper.
2) Some human in the loop architectures like CHAT and HAT (https://www.ijcai.org/proceedings/2017/0422.pdf) should give better results for the same framework.
3) It would be interesting to try out the framework suggested in this paper (L2T) in Imperfect information and partially observable settings.
4) As they have focused on data teaching exploring loss function teaching would be interesting.
Critique
While the conceptual framework of L2T is sound, the paper only experimentally demonstrates efficacy for data teaching which would seem to be the simplest to implement. The feasibility and effectiveness of teaching the loss function and hypothesis space are not explored in a real-world scenario. Also, this paper does not provide enough mathematical foundation to prove that this model can be generalized to other datasets and other general problems. The method presented here where the teacher model filters data does not seem to provide enough action space for the teacher model. Furthermore, the experimental results for data teaching suggest that the speed of convergence is the main improvement over other teaching strategies whereas the difference in accuracy less remarkable. The paper also assesses accuracy only by comparing L2T with NoTeach and SPL on the IMDB classification task, the improvement (or lack thereof) on the other classification tasks and teaching strategies is omitted. Again, this distinction is not possible to assess in loss function or hypothesis space teaching within the scope of this paper. They could have included larger datasets such as ImageNet and CIFAR100 in their experiments which would have provided some more insight.
Also, teaching should not be limited to data, loss function and hypothesis space. In a human teacher-student model, the teaching contents are concepts and logical rules, similar to weights of hidden layers in neural networks. How to transfer such knowledge is interesting to investigate.
The idea of having a generalizable teacher model to enhance student learning is admirable. In fact, the L2T framework is similar to the reinforcement learning actor-critic model, which is known to be effective. In general, one expects an effective teacher model would facilitate transfer learning and can significantly reduce student model training time. However, the T2L framework seems to fall short of that goal. Consider the CIFAR10 training scenario, the L2T model achieve 85% accuracy after 2 million training data, which is only about 3% more accuracy than a no-teacher model. Perhaps in the future, the L2T framework can improve and produce better performance.