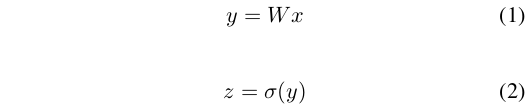Learning the Number of Neurons in Deep Networks
Introduction
Due to the availability of large-scale datasets and powerful computation, Deep Learning has made huge breakthroughs in many areas, like Language Models and Computer Vision. In deep neural networks, we need to determine the number of layers and the number of neurons in each layer, i.e, we need to determine the number of parameters, or complexity of the model. Typically, this is determined by errors manually. Currently, this is mostly achieved by manually tuning these hyper-parameters using validation data or building very deep networks. However, building a very deep model is still challenging, especially for very large datasets, which leads to high cost on memory and reduction in speed.
In this paper, we used an approach to automatically select the number of neurons in each layer when we learn the network. Our approach introduces a group sparsity regularizer on the parameters of the network, and each group acts on the parameters of one neuron, rather than trains an initial network as as pre-processing step(training shallow or thin networks to mimic the behaviour of deep ones [Hinton et al., 2014, Romero et al., 2015]). We set those useless parameters to zero, which cancels out the effects of a particular neuron. Therefore, our approach does not need to learn a redundant network successfully and then reduce its parameters, instead, it learns the number of relevant neurons in each layer and the parameters of those neurons simultaneously.
In the experiments on several image recognition datasets, we showed the effectiveness of our approach, which reduces the number of parameters by up to 80% compared to the complete model, and has no recognition accuracy loss at the same time. Actually, our approach even yields more effective and faster networks, and occupies less memory.
Related Work
The recent researches tend to build very deep networks. Building very deep networks means we need to learn more parameters, which leads to a significant cost on the memory of the equipment as well as the speed. Even though automatic model selection has developed in the past years by constructive and destructive approaches, there are some drawbacks. For constructive method, it starts a super shallow architecture, and then adds additional parameters [Bello, 1992]. A similar work that adds new layers to the initial shallow networks was successfully employed [Simonyan and Zisserman, 2014] at the process of learning. However, we know shallow networks have fewer parameters, so that it can not handle the non-linearities as effectively as the deep networks [Montufar et al., 2014], so shallow networks may easily get stuck by the bad optima. Therefore, the drawback of this method is that these networks may produce poor initializations for the later processes. The authors make this claim without ever providing any evidence for it. For destructive method, it starts by a deep network to reduce a significant number of redundant parameters [Denil et al., 2013, Cheng et al., 2015] while keeping its behaviour unchanged. Even though this technique has shown removing the redundant parameters [LeCun et al., 1990, Hassibi et al., 1993] or the neurons [Mozer and Smolensky, 1988, Ji et al., 1990, Reed, 1993] has little influence on the output, it requires the analysis of each parameter and neuron by network Hessian, which is very computationally expensive for large architectures. The main motivation of these works was to build a more compact network.
Particularly, building a compact network is a research focus for Convolutional Neural Networks(CNNs). Some works has proposed to decompose the filters of a pre-trained network into low-rank filters, which reduces the number of parameters [Jaderberg et al., 2014b, Denton et al., 2014, Gong et al., 2014]. The issue of this proposal is that we need to successfully train an initial deep network, since it acts as as post-processing step. [Weigend et al., 1991] and [Collins and Kohl, 2014] used direct training to develop regularizers that eliminate some of the parameters of the network. The problem is that the number of layers and neurons each layer is determined manually. A very similar work using the group lasso method for CNN was previously done in [Liu et al., 2015]. The big-picture idea appears to be very similar but they differ in details of methodology.
Model Training and Model Selection
In general, a deep network has L layers containing linear operations on their inputs, intertwined with activation functions. The activation function we generally use is Rectified Linear Units(RELU) or sigmoids. Suppose each layer l has $N_{l}$ neurons, and each of them has parameters $\Theta=(\theta_{l})_{1\leqslant{l}\leqslant{L}}$, where $\theta_{l}=({\theta^n _{l}})_{1\leqslant{n}\leqslant{N_{l}}}$ and where $\theta^n _{l}=[w_{l}^{n},b_{l}^{n}]$ is consisted of linear component $w_{l}^{n}$ and linear bias $b_{l}^{n}$. Given an input $x$, under the linear, on-linear and pooling operations, we obtain the output $\hat{y}=f(x,\theta)$, where $f(*)$ encodes the succession of linear, non-linear and pooling operations.
At the step of training, we have N input-output pairs ${(x_{i},y_{i})}_{1\leqslant{i}\leqslant{N}}$, and the loss function is given by $\ell(y_{i},f(x_{i},\Theta))$, which compares the predicted output with the ground-truth output. Generally, we choose logistic loss for classification and the square loss for regression. Therefore, learning the parameters of the network is equivalent to solving the optimization of the following: $$\displaystyle \min_{\Theta}\frac{1}{N}\sum_{i=1}^{N}\ell(y_{i},f(x_{i},\Theta))+\gamma(\Theta),$$ where $\gamma(\Theta)$ represents a regularizer on the network parameters. Our choice for the regularizer can be $\ell_{2}$-norm(i.e, weight decay) or $\ell_{1}$-norm. $\ell_{2}$-norm usually favours small parameter values, and $\ell_{1}$-norm can only delete those irrelevant parameters, but not the neurons. The goal in this paper is to automatically determine the number of neurons of each layer, but neither of the above techniques achieve this goal. Here, we make use of the group sparsity [Yuan and Lin., 2007] (starting from an overcomplete network and canceling the influence of some neurons). The regularizer, therefore, can be written as $$\gamma(\Theta)=\sum_{l=1}^{L}\beta_{l}\sqrt{P_{l}}\sum_{n=1}^{N_{l}}||\theta_{l}^{n}||_{2},$$ where $P_{l}$ means the size of the vector that includes the parameters of each neuron in layer $l$, and $\beta_{l}$ balances the influence of the penalty. In practice, we found the most effective way to select $\beta$ is a relatively small one for the first few layers, and a larger weight for the remaining layers. The reason we choose a small weight is that it can prevent deleting too much neurons in the first few layers, so that we have enough information for learning the remaining parameters. The original premise of this paper seemed to suggest a new method that was different from both the constructive and destructive methods described above. However, this approach of starting with an overcomplete network and training with group sparsity appears to be no different from destructive methods. The main contribution here is then the regularization function to act on entire neurons, which is in fairness an interesting approach.
The group sparsity helps us effectively remove some of the neurons, and also standard regularizers on the individual parameters are effective for the generalization purpose [Bartlett, 19996, Krogh and Hertz, 1992, Theodoridis, 2015, Collins and Kohli, 2014]. By this idea, we introduce sparse group Lasso, which considers a more generalised penalty that merges L1 norm in Lasso with the group lasso (i.e. "two-norm"). This leads to the production of a penalty which specifies solutions that are sparse enough both at an individual and group feature levels [1]. It specifies that the regularizer can be written as $$\gamma(\Theta)=\sum_{l=1}^{L}((1-\alpha)\beta_{l}\sqrt{P_{l}}\sum_{n=1}^{N_{l}}||\theta_{l}^{n}||_{2}+\alpha\beta_{l}||\theta_{l}||_{1},$$ where $\alpha\in[0,1]$. We find that if $\alpha=0$, then we have the group sparsity regularizer. In practice, we use both $\alpha=0$ and $\alpha=0.5$ in the experiments.
This reminds me of the relationships among Lasso regression, Ridge regression and Elastic Net regression. In lasso regression, the penalized residual sum of squares is composed of the regular residual sum of squared plus a L1 regularizer. In ridge regression, its penalized residual sum of squares is composed of the regular residual sum of squared plus a L2 regularizer. Finally, an elastic net regression is a combination of lasso regularizer and ridge regularizer, where its objective function is to optimize parameters by including both L1 and L2 norms.
To find the optimization, in this paper we use proximal gradient descent [Parikh and Boyed, 2014]. This approach iteratively takes a gradient step of size t with respect to the loss. The following is the algorithm for it:
We define proximal operator of f as $$prox_{f}(v)=\displaystyle \min_{x}(\frac{1}{2t}||x-v||_{2}^{2}+f(x))$$
Suppose we want to minimize $f(x)+g(x)$, and the proximal gradient method is given by $$x^{(k+1)}=prox_{t^{k}g}(x^{k}-t^{k}\nabla{f}(x^{k})), k=1,2,3...$$
Therefore, we can update our parameter by the above method as $$\tilde{\theta}_{l}^{n}=\displaystyle \min_{\theta_{l}^{n}}\frac{1}{2t}||\theta_{l}^{n}-\hat{\theta}_{l}^{n}||_{2}^{2}+\gamma(\Theta),$$ where $\hat{\theta}_{l}^{n}$ is the solution obtained from the general loss gradient. By the derivative of [Simon et al., 2013], we have a closed-form solution for this problem: $$\tilde{\theta}_{l}^{n}=(1-\frac{t(1-\alpha)\beta_{l}\sqrt{P_{l}}}{||S(\hat{\theta}_{l}^{n},t\alpha\beta_{l})||_{2})})_{+}S(\hat{\theta}_{l}^{n},t\alpha\beta_{l}),$$ where + refers to taking the maximum between the argument and 0, and $S(*)$ is $$S(a,b)=sign(a)(|a|-b)_{+}$$ In practice, we use stochastic gradient descent and work with mini-batches, and then update the variables of all the groups according to the closed-form of $\tilde{\theta}_{l}^{n}$. When the learning steps terminate, we remove the neurons whose parameters have gone to zero. Additionally, when examining fully-connected layers, the neurons acting on output of zeroed-out neurons of the previous layer also become useless, and are removed accordingly.
Experiment
Set Up
They use two large-scale image classification datasets, ImageNet [Russakovsky et al., 2015] and Places2-401 [Zhou et al., 2015]. They also conducted additional experiments on the ICDAR character recognition dataset of [Jaderberg et al., 2014a].
For ImageNet, they used the subset which contains 1000 categories, with 1.2 million training images and 50000 validation images. For Places2-401, it has more than 10 million images with 401 unique scene categories. 5000 to 30000 images are comprised into per category. Both architectures of these two datasets are based on the VGG-B network(BNet) [Simonyan and Zisserman, 2014] and on DecomposeMe8($Dec_{8}$) [ALvarez and Petersson, 2016]. BNet has 10 convolutional layers followed by 3 fully-connected layers. In the experiment, they remove the first 2 fully-connected layers, which we call $BNet^{C}$. $Dec_{8}$ contains 16 convolutional layers with 1D kernels, which can model 8 2D convolutional layers. Both models were trained for a total of 55 epochs with 12000 batches per epoch and a batch size of 48 and 180 for BNet and $Dec_{8}$, respectively. The learning rate was initialized by 0.01 and then multiplied by 0.1. They set $\beta_{l}$=0.102 for the first three layers and $\beta_{l}$=0.255 for the remaining ones.
For ICDAR dataset, it consists of 185639 training and 5198 test data split into 36 categories. The architecture here starts 6 1D convolutional layers with max-pooling, rather than 3 convolutional layers with a maxout layer [Goodfellow et al., 2013] after each convolution, followed by one fully-connected layer. They call their architecture as Dec3. The model was trained for a total of 45 epochs with a batch size of 256 and 1000 iterations per epoch. The learning rate was initialized by 0.1 and multiplied by 0.1 in the second, seventh and fifteenth epochs. They set $\beta_{l}$=5.1 for the first layer and $\beta_{l}$=10.2 for the remaining ones.
Results
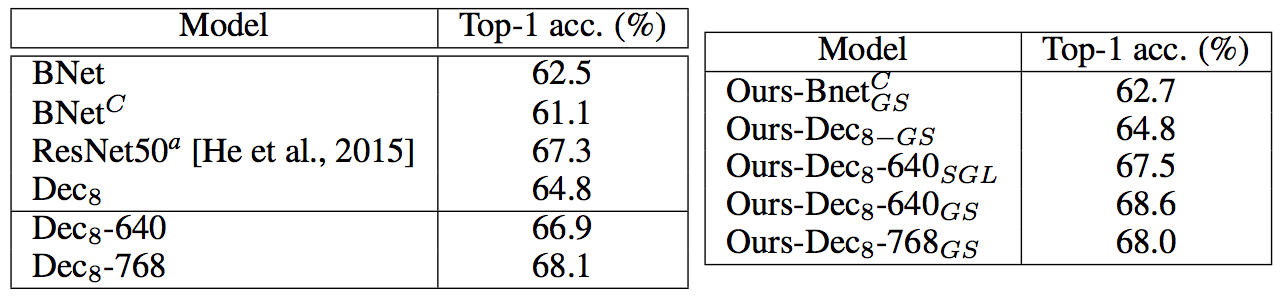
The above table show the accuracy comparisons between the original architectures and ours. For $Dec_{8}$ on the ImageNet dataset, we evaluated two additional models: $Dec_{8}-640$ with 640 neurons per layer and $Dec_{8}-768$ with 768 neurons per layer. $Dec_{8}-640_{SGL}$ means the sparse group Lasso regularizer with $\alpha=0.5$ and $Dec_{8}-640_{GS}$ represents the group sparsity regularizer. Note that all our architectures yield an improvement over the original network except $Dec_{8}-768$. For instance, Ours-$Bnet_{GS}^{C}$ increases the performance of 1.6% compared to $BNet^{C}$.
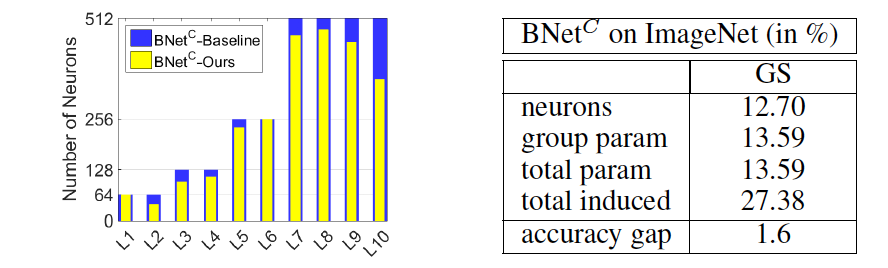
The above figures reports the reduced percentage of neurons/parameters with our approach for $BNet^{C}$ and $Dec_{8}$. For example, in the first figure, our approach reduces the number of neurons by over 12% and the number of parameters by around 14%, while improving the generalization ability of 1.6%(as indicated by accuracy gap). The left image in the first figure also shows that reduction in number of neurons is spread all the layers with the largest difference in the L10. For $Dec_{8}$, in the second figure, we find when we increase the number of neurons in each layer, the benefits of our approach become more significant. For instance, $Dec_{8}-640$ with group sparsity regularizer reduces the number of neurons by 10%, and of parameters by 12.48%. The left image in the second figure also shows that reduction in number of neurons is spread all the layers.
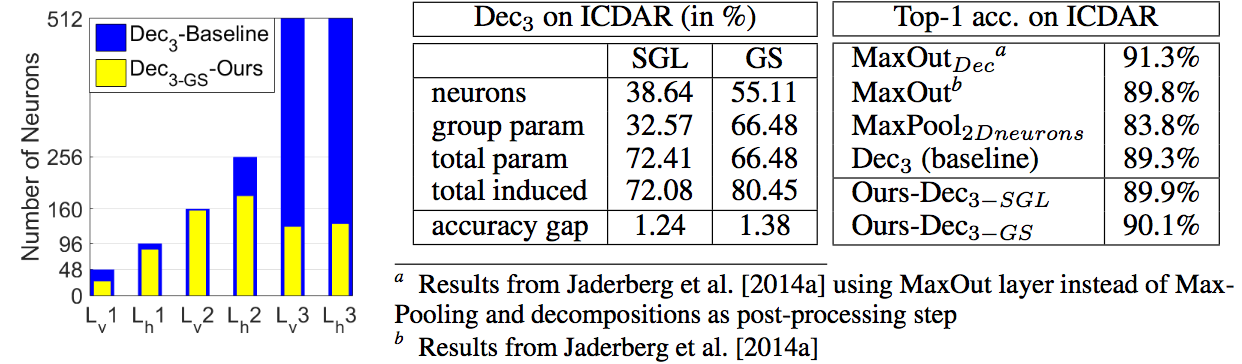
Finally, the above figure indicates the experiment results for ICDAR dataset. Here, we used the $Dec_{3}$ architecture, where the last two layers initially contain 512 neurons. The accuracy rate for $MaxPllo_{2Dneurons}$ is 83.8%, and accuracy rate for $Dec_{3}$ is 89.3%, which means 1D filters perform better than a network with 2D kernels. Our model on this dataset reduces 38.64% of neurons and totally up to 80% of the number of parameters with group sparsity regularizer.
All the above results evidence that our algorithm effectively removes the number of parameters and increases the model accuracy. Our algorithm of automatic model selection effectively performs on the classification task.
Analysis on Testing
Our algorithm does not remove neurons during the training time, however, we remove those neurons after training, which yields a smaller network at test time. This improvement not only reduces the number of parameters of the network, but also decreases the computational memory cost and increases the speed.
The above table reports the runtime, memory, as well as the percentage of reduced parameters after removing the zeroed-out neurons. The BNet and $Dec_{8}$ were tested on the dataset of ImageNet, while $Dec_{3-GS}$ was tested on the dataset of ICDAR. From the table, we find that all the models for the ImageNet and ICDAR have speeded up the runtime, for example, $Dec_{8}-768_{GS}$ on ImageNet data speeds up the runtime nearly 16% at the batch size of 8, and $Dec_{3}$ on ICDAR data speeds up nearly 50% at natch size of 16. For the percentage of parameters reduced, we find BNet, $Dec_{8}-640_{GS}$ and $Dec_{8}-768_{GS}$ have reduced 12.06%, 26.51%, and 46.73% respectively. More significantly, for $Dec_{3-GS}$, it reduces 82.35% of the parameters. All of these changes show the benefits at the testing time.
Conclusion
In this paper, we have introduced an approach that relies on group sparsity regularizer. This approach automatically determines the number of neurons in each layer of a deep network. From the experiments, we found our approach not only reduces the number of parameters in our model, but also saves the computation memory and increases the speed at test time. However, the limitation of our approach is that the number of layers in the network remains fixed.
Critique
The authors of the paper state that "...we assume that the parameters of each neuron in layer $l$ are grouped in a vector of size $P_{l}$ and where $\lambda_{l}$ sets the influence of the penalty. Note that, in the general case, this weight can be different for each layer $l$. In practice, however, we found most effective to have two different weights: a relatively small one for the first few layers, and a larger weight for the remaining ones. This effectively prevents killing too many neurons in the first few layers, and thus retains enough information for the remaining ones." However, the authors fail to present any guidance as to what gets counted as "the first few layers" and what the relative sizes for the two weights should be even after we have chosen the "first few layers". Indeed, such choice seems to be an unaccounted component of tuning the model but this receives scant attention in the current paper. Several numerical comparisons should be carried out to allow further discussion on this question.
The experiments could have included better baseline models to compare against. For example, how do we know the original model was not overly complex to begin with? It might have been a good idea for the authors to compare their group sparse lasso method against the naive method of (blindly) reducing the number of neurons in each layer by 10-20% just for a very preliminary check. Also, the author could have applied the theory of ridge and Lasso regression to analyze the effect of the regularization mathematically.
A rather reliable method of experimentation to compare the performance and accuracy has been left out. The authors have not stated any comparisons of this method with the Dropout method [Srivastava,2014], which is similar in terms of the physical effects on the network.
References
P. L. Bartlett. For valid generalization the size of the weights is more important than the size of the network. In NIPS, 1996.
M. G. Bello. Enhanced training algorithms, and integrated training/architecture selection for multilayer perceptron networks. IEEE Transactions on Neural Networks, 3(6):864–875, Nov 1992.
Yu Cheng, Felix X. Yu, Rogério Schmidt Feris, Sanjiv Kumar, Alok N. Choudhary, and Shih-Fu Chang. An exploration of parameter redundancy in deep networks with circulant projections. In ICCV, 2015.
I. J. Goodfellow, D. Warde-farley, M. Mirza, A. Courville, and Y. Bengio. Maxout networks. In ICML, 2013.
G. E. Hinton, O. Vinyals, and J. Dean. Distilling the knowledge in a neural network. In arXiv, 2014.
M. Jaderberg, A. Vedaldi, and A. Zisserman. Deep features for text spotting. In ECCV, 2014a.
M. Jaderberg, A. Vedaldi, and A. Zisserman. Speeding up convolutional neural networks with low rank expansions. In BMVC, 2014b.
N. Simon, J. Friedman, T. Hastie, and R. Tibshirani. A sparse-group lasso. Journal of Computational and Graphical Statistics, 2013.
H. Zhou, J. M. Alvarez, and F. Porikli. Less is more: Towards compact CNNs. In ECCV, 2016.
Group LASSO - https://pdfs.semanticscholar.org/f677/a011b2a912e3c5c604f6872b9716cc0b8aa0.pdf
Liu, Baoyuan, et al. "Sparse convolutional neural networks." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2015.
Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov. 2014. Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 15, 1 (January 2014), 1929-1958.
Derivation & Motivation of the Soft Thresholding Operator (Proximal Operator):