Learning Combinatorial Optimzation: Difference between revisions
| Line 45: | Line 45: | ||
== 4. Training == | == 4. Training == | ||
Formulating of Reinforcement learning | |||
1) States - S is a sequence of actions on a graph. | |||
2) Movement - transitioning to another node; Tag the node that was last used with feature x = 1 | |||
3) Actions - Is a node of the graph that isn't part of the sequence of actions. | |||
4) Rewards - reward function is defined as change in cost after action and movement. | |||
More specifically, | |||
r(S,v) = c(h(S'),G) - c(h(S),G); This represents change in cost evaluated from previous state to new state | |||
learning Algorithm: | learning Algorithm: | ||
Revision as of 17:08, 20 March 2018
Learning Combinatorial Optimization Algorithms Over Graphs
Group Members
Abhi (Graph Theory),
Alvin (actual paper)
Pranav (actual paper),
Daniel (Conclusion: performance, adv, disadv, criticism)
1. Introduction and Problem Motivation
(work in progress) One of the most common problems encountered today is a problem known as The Travelling Salesman Problem. The basic premise is that there is a salesman in a city, and he wants to go to people's doorsteps and sell them products, what is the best way to do it? There are a lot of different algorithms devised in the field of Combinatorics and Optimization that can be used to deal with this problem. For example, one solution might be to always visit the next nearest house, and try to sell the product to them, another solution might be to first get a list of possible candidates that may actually purchase your products, and try to visit all of those first, and then go to the original solution. A problem such as this takes a lot of time in order to solve, this problem is an example of a group of problems known as Graph Theory.
(work in progress) The current approach to tackling NP-hard combinatorial optimization problems are good heuristics or approximation algorithms. While these approaches have been adequate, it requires specific domain-knowledge behind each individual problem or additional trial-and-error in determining the tradeoff being finding an accurate or efficient heuristics function. However, if these problems are repeated solved, differing only in data values, perhaps we could apply learning on heuristics such that we automate this tedious task.
a) Graph Theory
Graph Theory is a set of problems where some sort of Spatial Analysis is needed in order to come up with a solution. Generally it is a shape which has several points (vertices), that are connected to each other through a series of edges(nodes). These problems have a common notation of: G=(V,E,w)
Where G is the Graph, V are the vertices, E is the edge, and w is the set of weights for the edges
The problems which the paper is trying to address are:
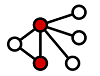
Minimum Vertex Cover: Given a ‘graph’ G, find the minimum number of vertices to tick, so that every single edge is covered. A quick example of this is below, you can see that when those 2 red vertices are ticked, every single edge is now touching a red vertex.
Maximum Cut: Given a ‘graph’ G,
Travelling Salesman Problem
2. Example Problems
Testing $X_i$ = 50
3. Representation
4. Training
Formulating of Reinforcement learning 1) States - S is a sequence of actions on a graph. 2) Movement - transitioning to another node; Tag the node that was last used with feature x = 1 3) Actions - Is a node of the graph that isn't part of the sequence of actions. 4) Rewards - reward function is defined as change in cost after action and movement.
More specifically, r(S,v) = c(h(S'),G) - c(h(S),G); This represents change in cost evaluated from previous state to new state
learning Algorithm:
To perform learning of the parameters, application of n-step Q learning and fitted Q-iteration is used.
Stepped Q-learning: This updates the function's parameters at each step by performing a gradient step to minimize the squared loss of the function. Generalizing to n-step Q learning, it addresses the issue of delayed rewards, where an immediate valuation of rewards may not be optimal. With this instance, 1 step updating of the parameters may not be optimal.
Fitted Q-learning: Is a faster learning convergence when used on top of a neural network. In contrast to updating Q function sample by sample, it updates function with batches of samples from data set instead of singular samples.
5. Results and Criticisms
The paper proposes a solution that uses a combination of reinforcement learning and graph embedding to improve current methods of solving graph optimization problems. However, the graph embedding network the authors use is called structure2vec (S2V). S2V takes a graph as input and converts the properties of the nodes in the graph as features. Some of these properties or features include a node’s graph neighbourhood which may or may not be useful depending on the problem. In particular, knowing a node’s neighbourhood is useful in problems such as Minimum Vertex Cover or Maximum Cut, however it may not be as useful in problems such as Traveling Salesman Problem. Another criticism for the paper is in their choice of reinforcement learning algorithm. The authors decide to use the Deep Q Learning (DQN) algorithm in their experiments and tests. However, they did not consider using Asynchronous Advantage Actor Critic (A3C) which is a fast and popular Reinforcement learning algorithm that provides an simple and lightweight advantage to its processing.
6. Conclusions
The machine learning framework the authors propose is a solution to NP-hard graph optimization problems that have a large amount of instances that need to be computed. Where the problem structure remains largely the same except for specific data values. Such cases are common in the industry where large tech companies have to process millions of requests per second and can afford to invest in expensive pre-computation if it speeds up real-time individual requests. Through their experiments and performance results the paper has shown that their solution could potentially lead to faster development and increased runtime efficiency of algorithms for graph problems.
7. Source
Hanjun Dai, Elias B. Khalil, Yuyu Zhang, Bistra Dilkina, Le Song. Learning Combinatorial Optimization Algorithms over Graphs. In Neural Information Processing Systems, 2017