Incremental Boosting Convolutional Neural Network for Facial Action Unit Recognition
Introduction
Facial expression is one of the most natural ways that human beings express emotion. The Facial Action Coding System (FACS) attempts to systemically categorize each facial expression by specifying a basic set of muscle contractions or relaxations, formally called Action Units (AUs). The codes are categorized into main, head movement, eye movement, visibility and gross behaviour . For example, "AU 1" stands for the inner portion of the brows being raised, and "AU 6" stands for the cheeks being raised. Such a framework would help us describe any facial expression as possibly a combination of different AUs. The complete list of AUs in the FACS can be seen here. However, during the course of an average day, most human beings do not experience drastically varying emotions and therefore their facial expressions might change only subtly. Additionally, there might also be a lot of subjectivity involved if this task were to be done manually. To address these issues, it is imperative to automate this task. Moreover, automating AU recognition also has potential applications in human-computer interaction (HCI), online education, interactive gaming, among other domains.
Because of the recent advancements in object detection and categorization tasks, CNNs are an appealing go-to for the facial AU recognition task described above. However, compared to the former, the training sets available for the AU recognition task are not very large, and therefore the learned CNNs suffer from overfitting. To overcome this problem, this work builds on the idea of integrating boosting within CNN. Boosting is a technique wherein multiple weak learners are combined together to yield a strong learner. Moreover, this work also modifies the mechanics of learning a CNN by breaking large datasets in mini-batches. Typically, in a batch strategy, each iteration uses a batch only to update the parameters and the features learned in that iteration are discarded for subsequent iterations. Herein the authors incorporate incremental learning by building a classifier that incrementally learns from all the iterations/batches. Hence the genesis of the name Incremental Boosting - Convolutional Neural Network (IB-CNN) is justified. The IB-CNN introduced here outperforms the state-of-the-art CNNs on four standard AU-coded databases.
Related Work
There have been many papers that use manually designed features to the AU-recognition task, unlike the CNN-based methods which integrate feature learning. Some of them are Gabor Wavelets, Local Binary Patterns (LBP), Histogram of Oriented Gradients (HOG), Scale Invariant Feature Transform (SIFT) features, Histograms of Local Phase Quantization (LPQ), and their spatiotemporal extensions. One of the major breakthroughs to reduce overfitting in CNNs was dropout, introduced by Hinton et al, which randomly drops certain neurons. This work can be seen as a refinement of the previous random dropout approach in the sense that only neurons with no contribution towards classification are dropped, while retaining the more discriminative neurons. Moreover, adopting a batch strategy with incremental learning also circumvents the issue of not-so-large datasets.
Methodology
CNNs
Convolutional Neural Networks are neural networks that contain at least one convolution layer. Typically, the convolution layer is accompanied with a pooling layer. A convolution layer, as the name suggests, convolves the input matrix (or tensor) with a filter (or kernel). This operation produces a feature map (or activation map) that, roughly speaking, shows the presence or absence of the filter in the image. Note that the parameters in the kernel are not preset and are learned. A pooling layer reduces the dimensionality of the data by summarizing the activation map by some means (such as max or average). Following this, the matrix (or tensor) data is then vectorized using a fully-connected (FC) layer. The neurons in the FC layer have connections to all the activations in the previous layer. Finally, there is a decision layer that has as many neurons as the number of classes. The decision layer decides the class based on computing a score function using the activations of the FC layer. Generally, an inner-product score function is used, which is replaced by the boosting score function in this work.
Boosting Method
Ever since boosting method was first officially introduced in the 1990s, it has become one of the most powerful learning method to improve model performance. The fundamental boosting algorithm that was introduced Freund and Schapire in 1995: AdaBoost has evolved into many much more sophisticated boosting methods (Freund & Schapire, 1997). The essential idea of boosting is to use a weighted combination of a sequence of weak classifiers to make a strong one. The key point to this process is after each iteration of data modification (through any type of model), the boosting algorithm will place more weight on observations that are difficult to classify correctly. Therefore, those “weak” classifiers can then focus on those observations that are hard to predict (Hastie, Tibshirani, & Friedman, 2017) These explanations can be summarized using the following formula:
[math]\displaystyle{ G(x) = sign(\sum\limits_{m=1}^M \alpha_m G_m(x)) }[/math] Where [math]\displaystyle{ \alpha_m }[/math] are computed by boosting algorithm and [math]\displaystyle{ G_m(x) }[/math] denotes a weak classifier.
Boosting CNN
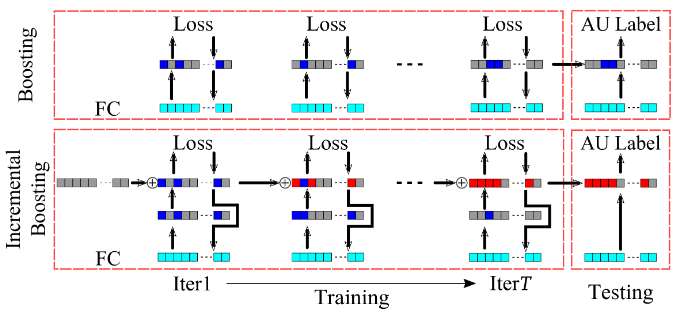
Let $X = [x_1, \dots, x_M]$ denote the activation features of a training data batch of size $M$, where each $x_i$ has $K$ activation features. Also, let $Y = [y_1, \dots , y_M]$ denote the corresponding labels, i.e. each $y_i \in \{-1, +1\}$. In other words, the vector $x_i$ contains all the activations of the FC layer, which is typically multiplied with the weights corresponding to the connections between the FC layer and the decision layer. However, as mentioned earlier, this work achieves that same task of scoring via boosting as opposed to computing the inner product. Denoting the weak classifiers by $h(\cdot)$, we obtain the strong classifier as: \begin{equation} \label{boosting} H(x) = \sum\limits_{i = 1}^K \alpha_i h(x_{ij}; \lambda_j) \end{equation} where $x_{ij}$ is the $j^{th}$ activation feature of the $i^{th}$ input. Moreover, $\alpha_j \geq 0$ denotes the weight of the $j^{th}$ weak classifier and $\sum\limits_{i=1}^K\alpha_i = 1$. Here we define $h(\cdot)$ to be a differentiable surrogate for the sign function as: \begin{equation} h(x_{ij}; \lambda_j) = \dfrac {f(x_{ij}; \lambda_j)}{\sqrt{f(x_{ij}; \lambda_j)^2 + \eta^2}} \end{equation} where $f(x_{ij}; \lambda_j)$ denotes a decision-stump (one-level decision tree) with $\lambda_j$ being the threshold. The parameter $\eta$ controls the slope of the function $\dfrac {f(\cdot)}{\sqrt{f(\cdot)^2 + \eta^2}}$. Note that for a certain strong classifier $H$ if a certain $\alpha_i = 0$, then the activation feature $x_i$ has no contribution to the output of the classifier $H$. In other words, the corresponding neuron can be considered to be inactive. (Refer to the Figure for a schematic diagram of B-CNN.)
Incremental Boosting
In vanilla B-CNN, the information learned in a certain batch, i.e. the weights and the thresholds of the active neurons is discarded for subsequent batches. To address this issue, in this work the idea of incremental learning is incorporated. Formally, the incremental strong classifier at the $t^{th}$ iteration, $H_I^t$, is given as: \begin{equation} \label{incr} H_I^t(x_i^t) = \frac{(t-1)H_I^{t-1}(x_i^t) + H^t(x_i^t)}{t} \end{equation} where $H_I^{t-1}$ is the incremental strong classifier obtained at the $(t-1)^{th}$ iteration and $H^t$ is the boosted strong classifier at the $t^{th}$ iteration. Manipulating the equations, we obtain: \begin{equation} H_I^t(x_i^t) = \sum\limits_{j=1}^K \alpha_j^t h^t(x_{ij}; \lambda_j^t);\quad \alpha_j^t = \frac{(t-1)\alpha_j^{t-1}+\hat{\alpha}_j^t}{t} \end{equation} where $\hat{\alpha}_j^t$ is the weak classifier weight calculated in the $t^{th}$ iteration by boosting and $\alpha_j^t$ is the cumulative weight considering previous iterations. (Refer to the Figure for a schematic diagram of IB-CNN.) Typically, boosting algorithms minimize an objective function that captures the loss of the strong classifier. However, the loss of the strong classifier may be dominated by some weak classifiers with large weights, which might lead to overfitting. Therefore, to exercise better control, the loss function at a certain iteration $t$, $\epsilon^{IB}$ is expressed as a convex combination of the loss of the incremental strong classifier at iteration $t$ and the loss of the weak classifiers determined at iteration $t$. That is, \begin{equation} \epsilon^{IB} = \beta\epsilon_{strong}^{IB} + (1-\beta)\epsilon_{weak} \end{equation} where \begin{equation} \epsilon_{strong}^{IB} = \frac{1}{M}\sum\limits_{i=1}^M[H_I^t(x_i^t)-y_i^t]^2;\quad \epsilon_{weak} = \frac{1}{MN}\sum\limits_{i=1}^M\sum\limits_{\substack{1 \leq j \leq K \\ \alpha_j > 0}}[h(x_{ij}, \lambda_j)-y_i]^2. \end{equation}
To learn the parameters of the IB-CNN, stochastic gradient descent is used, and the descent directions are obtained by differentiating the loss above with respect to the parameters $x_{ij}^t$ and $\lambda_j^t$ as follows: \begin{equation} \dfrac{\partial \epsilon^{IB}}{\partial x_{ij}^t} = \beta\dfrac{\partial \epsilon_{strong}^{IB}}{\partial H_I^t(x_i^t)}\dfrac{\partial H_I^t(x_i^t)}{\partial x_{ij}^t} + (1-\beta)\dfrac{\partial \epsilon_{weak}^{IB}}{\partial h^t(x_{ij}^t;\lambda_j^t)}\dfrac{\partial h^t(x_{ij}^t;\lambda_j^t)}{\partial x_{ij}^t} \\ \dfrac{\partial \epsilon^{IB}}{\partial \lambda_j^t} = \beta\sum\limits_{i = 1}^M\dfrac{\partial \epsilon_{strong}^{IB}}{\partial H_I^t(x_i^t)}\dfrac{\partial H_I^t(x_i^t)}{\partial x_{ij}^t} + (1-\beta)\sum\limits_{i = 1}^M\dfrac{\partial \epsilon_{weak}^{IB}}{\partial h^t(x_{ij}^t;\lambda_j^t)}\dfrac{\partial h^t(x_{ij}^t;\lambda_j^t)}{\partial x_{ij}^t} \end{equation} where $\frac{\partial \epsilon^{IB}}{\partial x_{ij}^t}$ and $\frac{\partial \epsilon^{IB}}{\partial \lambda_j^t}$ only need to be calculated for the active neurons. Overall, the pseudocode for the incremental boosting algorithm for the IB-CNN is as follows.
Input: The number of iterations (mini-batches) $T$ and activation features $X$ with the size of $M \times K$, where $M$ is the number of images in a mini-batch and $K$ is the dimension of the activation feature vector of one image.
$\quad$ 1: for each input activation $j$ from $1$ to $K$ do
$\quad$ 2: $\quad \alpha_j^1 = 0$
$\quad$ 3: end for
$\quad$ 4: for each mini-batch $t$ from $1$ to $T$ do
$\quad$ 5: $\quad$ Feed-forward to the fully connected layer;
$\quad$ 6: $\quad$ Select active features by boosting and calculate weights $\hat{\alpha}^t$ based on the standard AdaBoost;
$\quad$ 7: $\quad$ Update the incremental strong classifier;
$\quad$ 8: $\quad$ Calculate the overall loss of IB-CNN;
$\quad$ 9: $\quad$ Backpropagate the loss based using the SGD equations;
$\quad$ 10: $\quad$ Continue backpropagation to lower layers;
$\quad$ 11: end for
Experiments
Experiments have been conducted on four AU-coded databases whose details are as follows.
1. CK database: contains 486 image sequences from 97 subjects, and 14 AUs.
2. FERA2015 SEMAINE database: contains 31 subjects with 93,000 images and 6 AUs.
3. FERA2015 BP4D database: contains 41 subjects with 146,847 images and 11 AUs.
4. DISFA database: contains 27 subjects with 130,814 images and 12 AUs.
The images are subjected to some preprocessing initially in order to scale and align the face regions, and to also remove out-of-plane rotations.
The IB-CNN architecture is as follows. The authors have used the pretrained CIFAR10 model. The CIFAR model is a model whose CNN layers are trained for tiny images (32x32x3). Using pretrained imagenet weights could have resulted in better results since the resolutions of the experiment are more coherent with imagenet hyperparameters. The first two layers are convolutional layers having 32 filters with a size of 5 X 5 with a stride of 1. The activation maps then are sent to a rectified layer which is then followed by an average pooling layer with a stride of 3. This is followed again by a convolutional layer with 64 filters of size 5 X 5, the activation maps from which are sent into an FC layer with 128 nodes. The FC layer in turn feeds into the decision layer via the boosting mechanism.
The following table compares the performance of the IB-CNN with other state-of-the-art methods that include CNN-based methods.
insert table
Lastly, brief arguments are provided supporting the robustness of the IB-CNN to variations in: the slope parameter $\eta$, the number of input neurons, and the learning rate $\gamma$.
Conclusion
To deal with the issue of relatively small-sized datasets in the domain of facial AU-recognition, the authors incorporate boosting and incremental learning to CNNs. Boosting helps the model to generalize well by preventing overfitting, and incremental learning exploits more information from the mini-batches but retaining more learned information. Moreover, the loss function is also changed so as to have more control over fine-tuning the model. The proposed IB-CNN shows improvement over the existent methods over four standard databases, showing a pronounced improvement in recognizing infrequent AUs.
There are two immediate extensions to this work. Firstly, the IB-CNN may be applied to other problems wherein the data is limited. Secondly, the model may also be modified to go beyond binary classification and achieve multiclass boosted classification. Modern day AdaBoost allows the weights $\alpha_i$, where i is the classifier, to be negative as well which gives the intuition that, "do exactly opposite of what this classifier says". In IB-CNN, the authors have restricted the weights of the input (FC units) to the boosting to be $\geq 0$. Considering that the IB-CNN is advantageous to models where datasets of a certain class are less in number, it would help the CNN to identify activation units in the FC layer which consistently contribute to wrong prediction so that their consistency can be utilized in making correct predictions. From the AdaBoost classifier weight update, we conclude that the classifiers which should be considered to be inactive are those which cannot be relied upon i.e. those which contribute consistently nearly equal amount of correct and incorrect predictions.
References
1. Han, S., Meng, H., Khan, A. S., Tong, Y. (2016) "Incremental Boosting Convolutional Neural Network for Facial Action Unit Recognition". NIPS.
2. Tian, Y., Kanade, T., Cohn, J. F. (2001) "Recognizing Action Units for Facial Expression Analysis". IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 23., No. 2.
3. Facial Action Coding System - https://en.wikipedia.org/wiki/Facial_Action_Coding_System