IPBoost
Presented by
Casey De Vera, Solaiman Jawad
Introduction
Boosting is an important and by now standard technique in classification to combine several “low accuracy” learners, so-called base learners, into a “high accuracy” learner, a so-called boosted learner. Pioneered by the AdaBoost approach of Freund & Schapire, in recent decades there has been extensive work on boosting procedures and analyses of their limitations.
In a nutshell, boosting procedures are (typically) iterative schemes that roughly work as follows:
for [math]\displaystyle{ t= 1, \cdots, T }[/math] do the following:
- Push weight of the data distribution [math]\displaystyle{ \mathcal D_t }[/math] towards misclassified examples leading to [math]\displaystyle{ \mathcal D_{t+1} }[/math]
- Evaluate performance of [math]\displaystyle{ \mu_t }[/math] by computing its loss.
- Train a learner [math]\displaystyle{ \mu_t }[/math] from a given class of base learners on the data distribution [math]\displaystyle{ \mathcal D_t }[/math]
Finally, the learners are combined by some form of voting (e.g., soft or hard voting, averaging, thresholding).

A close inspection of most boosting procedures reveals that they solve an underlying convex optimization problem over a convex loss function by means of coordinate gradient descent. Boosting schemes of this type are often referred to as convex potential boosters. These procedures can achieve exceptional performance on many data sets if the data is correctly labeled. In fact, in theory, provided the class of base learners is rich enough, a perfect strong learner can be constructed that has accuracy 1, however clearly such a learner might not necessarily generalize well. Boosted learners can generate quite some complicated decision boundaries, much more complicated than that of the base learners. Here is an example from Paul van der Laken’s blog / Extreme gradient boosting gif by Ryan Holbrook. Here data is generated online according to some process with optimal decision boundary represented by the dotted line and XGBoost was used learn a classifier:
Recently non-convex optimization approaches for solving machine learning problems have gained significant attention. In this paper we explore non-convex boosting in classification by means of integer programming and demonstrate real-world practicability of the approach while circumventing shortcomings of convex boosting approaches. The paper reports results that are comparable to or better than the current state-of-the-art.
Motivation
In reality we usually face unclean data and so-called label noise, where some percentage of the classification labels might be corrupted. We would also like to construct strong learners for such data. However if we revisit the general boosting template from above, then we might suspect that we run into trouble as soon as a certain fraction of training examples is misclassified: in this case these examples cannot be correctly classified and the procedure shifts more and more weight towards these bad examples. This eventually leads to a strong learner, that perfectly predicts the (flawed) training data, however that does not generalize well anymore. This intuition has been formalized by [LS] who construct a “hard” training data distribution, where a small percentage of labels is randomly flipped. This label noise then leads to a significant reduction in performance of these boosted learners; see tables below. The more technical reason for this problem is actually the convexity of the loss function that is minimized by the boosting procedure. Clearly, one can use all types of “tricks” such as early stopping but at the end of the day this is not solving the fundamental problem.
IPBoost: Boosting via Integer Programming
Integer Program Formulation
Let [math]\displaystyle{ (x_1,y_1),\cdots, (x_N,y_N) }[/math] be the training set with points [math]\displaystyle{ x_i \in \mathbb{R}^d }[/math] and two-class labels [math]\displaystyle{ y_i \in \{\pm 1\} }[/math]
- class of base learners: [math]\displaystyle{ \Omega :=\{h_1, \cdots, h_L: \mathbb{R}^d \rightarrow \{\pm 1\}\} }[/math] and [math]\displaystyle{ \rho \ge 0 }[/math] be given.
- error function [math]\displaystyle{ \eta }[/math]
Our boosting model is captured by the integer programming problem. We can call this our primal problem:
$$ \begin{align*} \min &\sum_{i=1}^N z_i \\ s.t. &\sum_{j=1}^L \eta_{ij}\lambda_k+(1+\rho)z_i \ge \rho \ \ \ \forall i=1,\cdots, N \\ &\sum_{j=1}^L \lambda_j=1, \lambda \ge 0,\\ &z\in \{0,1\}^N. \end{align*}$$
Solution of the IP using Column Generation
The goal of column generation is to provide an efficient way to solve the linear programming relaxation of the primal by allowing the [math]\displaystyle{ z_i }[/math] variables to assume fractional values. Moreover, columns, i.e., the base learners, [math]\displaystyle{ \mathcal L \subseteq [L]. }[/math] are left out because there are too many to handle efficiently and most of them will have their associated weight equal to zero in the optimal solution anyway. TO generate columns, a branch and bound framework is used. To check the optimality of an LP solution, a subproblem, called the pricing problem, is solved to try to identify columns with a profitable reduced cost. If such columns are found, the LP is reoptimized. Branching occurs when no profitable columns are found, but the LP solution does not satisfy the integrality conditions. Branch and price applies column generation at every node of the branch and bound tree.
The restricted master primal problem is
$$ \begin{align*} \min &\sum_{i=1}^N z_i \\ s.t. &\sum_{j\in \mathcal L} \eta_{ij}\lambda_j+(1+\rho)z_i \ge \rho \ \ \ \forall i \in [N]\\ &\sum_{j\in \mathcal L}\lambda_j=1, \lambda \ge 0,\\ &z\in \{0,1\}^N. \end{align*}$$
Its restricted dual problem is:
$$ \begin{align*}\max \rho &\sum^{N}_{i=1}w_i + v - \sum^{N}_{i=1}u_i \\ s.t. &\sum_{i=1}^N \eta_{ij}w_k+ v \le 0 \ \ \ \forall j \in L \\ &(1+\rho)w_i - u_i \le 1 \ \ \ \forall i \in [N] \\ &w \ge 0, u \ge 0, v\ free\end{align*}$$
Furthermore, there is a pricing problem used to determine, for every supposed optimal solution of the dual, whether the solution is actually optimal, or whether further constraints need to be added into the primal solution. This pricing problem can be expressed as follows:
$$ \sum_{i=1}^N \eta_{ij}w_k^* + v^* > 0 $$
The optimal misclassification values are determined by a branch-and-price process that branches on the variables [math]\displaystyle{ z_i }[/math] and solves the intermediate LPs using column generation.
Algorithm
[math]\displaystyle{ D = \{(x_i, y_i) | i ∈ I\} ⊆ R^d × \{±1\} }[/math], class of base learners [math]\displaystyle{ Ω }[/math], margin [math]\displaystyle{ \rho }[/math]
Output: Boosted learner [math]\displaystyle{ \sum_{j∈L^∗}h_jλ_j^* }[/math] with base learners [math]\displaystyle{ h_j }[/math] and weights [math]\displaystyle{ λ_j^* }[/math]
- [math]\displaystyle{ T ← \{([0, 1]^N, \emptyset)\} }[/math] // set of local bounds and learners for open subproblems
- [math]\displaystyle{ U ← \infty, L^∗ ← \emptyset }[/math] // Upper bound on optimal objective
- while [math]\displaystyle{ \ T \neq \emptyset }[/math] do
- Choose and remove [math]\displaystyle{ (B,L) }[/math] from [math]\displaystyle{ T }[/math]
- repeat
- Solve the primal IP using the local bounds on [math]\displaystyle{ z }[/math] in [math]\displaystyle{ B }[/math] with optimal dual solution [math]\displaystyle{ (w^∗, v^∗, u^∗) }[/math]
- Find learner [math]\displaystyle{ h_j ∈ Ω }[/math] satisfying the pricing problem. // Solve pricing problem.
- until [math]\displaystyle{ h_j }[/math] is not found
- Let [math]\displaystyle{ (\widetilde{λ} , \widetilde{z}) }[/math] be the final solution of the primal IP with base learners [math]\displaystyle{ \widetilde{L} = \{j | \widetilde{λ}_j \gt 0\} }[/math]
- if [math]\displaystyle{ \widetilde{z} ∈ \mathbb{Z}^N }[/math] and [math]\displaystyle{ \sum^{N}_{i=1}\widetilde{z}_i \lt U }[/math] then
- [math]\displaystyle{ U ← \sum^{N}_{i=1}\widetilde{z}_i, L^∗ ← \widetilde{L}, λ^∗ ← \widetilde{\lambda} }[/math] // Update best solution.
- else
- Choose [math]\displaystyle{ i ∈ [N] }[/math] with [math]\displaystyle{ \widetilde{z}_i \notin Z }[/math]
- Set [math]\displaystyle{ B_0 ← B ∩ \{z_i ≤ 0\}, B_1 ← B ∩ \{z_i ≥ 1\} }[/math]
- Add [math]\displaystyle{ (B_0,\widetilde{L}), (B_1,\widetilde{L}) }[/math] to [math]\displaystyle{ T }[/math]. // Create new branching nodes.
- end if
- end while
- Optionally sparsify final solution [math]\displaystyle{ L^* }[/math]
Results and Performance
All tests were run on identical Linux clusters with Intel Xeon Quad Core CPUs, with 3.50GHz, 10 MB cache, and 32 GB of main memory.
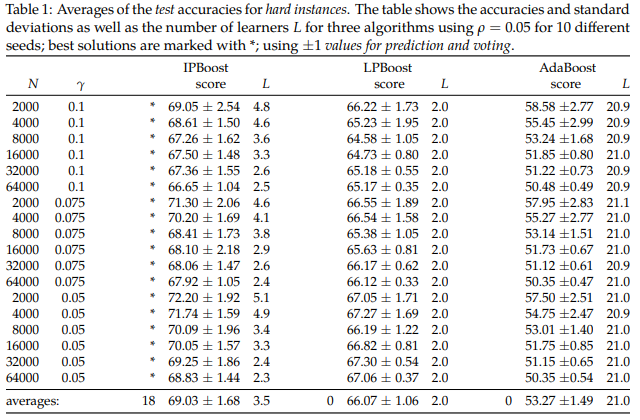
The following results reflect IPBoost's performance on hard instances. Note that by hard instances, we mean a binary classification problem with predefined labels. These examples are tailored to using the ±1 classification from learners. On every hard instance sample, IPBoost significantly outperforms both LPBoost and AdaBoost (although implementations depending on the libraries used have often caused results to differ slightly). For the considered instances the best value for the margin ρ was 0.05 for LPBoost and IPBoost; AdaBoost has no margin parameter. The accuracy reported is test accuracy recorded across various different walkthroughs of the algorithm, while [math]\displaystyle{ L }[/math] denotes the aggregate number of learners required to find the optimal learner, N is the number of points and [math]\displaystyle{ \gamma }[/math] refers to the noise level.
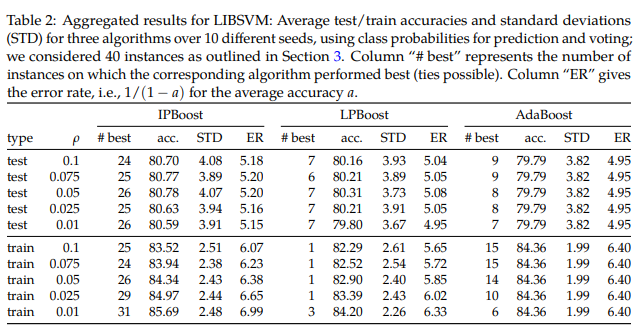
For the next table, the classification instances from LIBSVM data sets available at [1]. We report accuracies on the test set and train set, respectively. In each case, we report the averages of the accuracies over 10 runs with a different random seed and their standard deviations. We can see IPboost again outperforming LPBoost and AdaBoost significantly. Solving Integer Programming problems is no doubt more computationally expensive than traditional boosting methods like AdaBoost. The average run time of IPBoost (for ρ = 0.05) being 1367.78 seconds, as opposed to LPBoost's 164.35 seconds and AdaBoost's 3.59 seconds reflects exactly that. However, on the flip side, we gain much better stability in our results, as well as higher scores across the board for both training and test sets.
Conclusion
IP-boosting avoids the bad performance on well-known hard classes and improves upon LP-boosting and AdaBoost on the LIBSVM instances where even a few percent improvement is valuable. The major drawback is that the running time with the current implementation is much longer. Nevertheless, the algorithm can be improved in the future by solving the intermediate LPs only approximately and deriving tailored heuristics that generate decent primal solutions to save on time.
Suffice to say, the approach is suited very well to an offline setting in which training may take time and where even a small improvement is beneficial or when convex boosters have egregious behaviour.
References
- Pfetsch, M. E., & Pokutta, S. (2020). IPBoost--Non-Convex Boosting via Integer Programming. arXiv preprint arXiv:2002.04679.
- Freund, Y., & Schapire, R. E. (1995, March). A desicion-theoretic generalization of on-line learning and an application to boosting. In European conference on computational learning theory (pp. 23-37). Springer, Berlin, Heidelberg. pdf