Hierarchical Question-Image Co-Attention for Visual Question Answering: Difference between revisions
No edit summary |
No edit summary |
||
| Line 159: | Line 159: | ||
|} | |} | ||
These co-attention mechanisms are executed at all three levels of the question hierarchy yielding $\hat{v}^r$ and $\hat{q}^r$ | These co-attention mechanisms are executed at all three levels of the question hierarchy yielding $\hat{v}^r$ and $\hat{q}^r$ | ||
where $r$ is levels in hierarchy i.e. $r \in \{w,p,s\}$ (refer to [[: | where $r$ is levels in hierarchy i.e. $r \in \{w,p,s\}$ (refer to [[:Notations]] section). Following sub-sections explains both the | ||
co-attention mehcnaism throughly. | co-attention mehcnaism throughly. | ||
Revision as of 10:50, 22 November 2017
Paper Summary
| Conference |
|
| Authors | Jiasen Lu, Jianwei Yang, Dhruv Batra, Devi Parikh |
| Abstract | A number of recent works have proposed attention models for Visual Question Answering (VQA) that generate spatial maps highlighting image regions relevant to answering the question. In this paper, we argue that in addition to modeling "where to look" or visual attention, it is equally important to model "what words to listen to" or question attention. We present a novel co-attention model for VQA that jointly reasons about image and question attention. In addition, our model reasons about the question (and consequently the image via the co-attention mechanism) in a hierarchical fashion via a novel 1-dimensional convolution neural networks (CNN). Our model improves the state-of-the-art on the VQA dataset from 60.3% to 60.5%, and from 61.6% to 63.3% on the COCO-QA dataset. By using ResNet, the performance is further improved to 62.1% for VQA and 65.4% for COCO-QA. |
Introduction
Visual Question Answering (VQA) is a recent problem in computer vision and natural language processing that has garnered a large amount of interest from the deep learning, computer vision, and natural language processing communities. In VQA, an algorithm needs to answer text-based questions about images in natural language as illustrated in Figure 1.
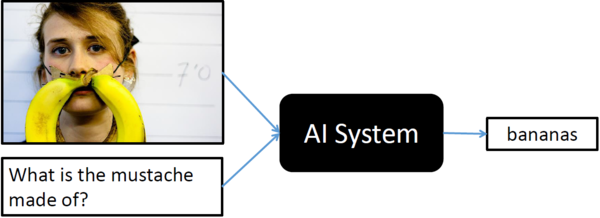
Recently, visual-attention based models have gained traction for VQA tasks, where the attention mechanism typically produces a spatial map highlighting image regions relevant for answering the visual question about the image. However, to correctly answer the question, machine not only needs to understand or "attend" regions in the image but also the parts of question as well. In this paper, authors have proposed a novel co-attention technique to combine "where to look" or visual-attention along with "what words to listen to" or question-attention VQA allowing their model to jointly reasons about image and question thus improving upon existing state of the art results.
"Attention" Models
You may skip this section if you already know about "attention" in context of deep learning. Since this paper talks about "attention" almost everywhere, I decided to put this section to give very informal and brief introduction to the concept of the "attention" mechanism specially visual "attention", however, it can be expanded to any other type of "attention".
Visual attention in CNN is inspired by the biological visual system. As humans, we have ability to focus our cognitive processing onto a subset of the environment that is more relevant for the given situation. Imagine, you witness a bank robbery where robbers are trying to escape on a car, as a good citizen, you will immediately focus your attention on number plate and other physical features of the car and robbers in order to give your testimony later. Such selective visual attention for a given context can also be implemented on traditional CNNs making them more superior for certains tasks and it even helps algorithm designer to visualize what localized features were more important than others.
Role of Visual Attention in VQA
This section is not a part of the actual paper that is been summarized, however, it gives an overview of how visual attention can be incorporated in training of a network for VQA tasks, eventually, helping readers to absorb and understand actual proposed ideas from the paper more effortlessly.
Generally for implementing attention, network tries to learn the conditional distribution [math]\displaystyle{ P_{i \in [1,n]}(Li|c) }[/math] representing individual importance for all the features extracted from each of the dsicrete [math]\displaystyle{ n }[/math] locations within the image conditioned on some context vector [math]\displaystyle{ c }[/math]. In order words, given [math]\displaystyle{ n }[/math] features [math]\displaystyle{ L_i = [L_0, L_1, ..., L_n] }[/math] from [math]\displaystyle{ n }[/math] different regions within the image(top-left, top-middle, top-right, and so on), then "attention" module learns a parameteric function [math]\displaystyle{ F(c;\theta) }[/math] that outputs importance of each of these individual feature for a given context vector [math]\displaystyle{ c }[/math] or outputs a discrete probability distribution of size [math]\displaystyle{ n }[/math], can be achived by [math]\displaystyle{ softmax(n) }[/math].
In order to incorporate the visual attention in VQA task, one can define context vector [math]\displaystyle{ c }[/math] as a representation of the visual question asked by an user (using RNN perhaps LSTM) and generate a localized attention map which can than be used for end-to-end training purposes as shown in Figure 2. Most work that exists in literature regarding use of visual-attention in VQA tasks are generally further specialization of such similar ideas.

Motivation
So far, all attention models for VQA in literature have focused on the problem of identifying "where to look" or visual attention. In this paper, authors argue that the problem of identifying "which words to listen to" or question attention is equally important. Consider the questions "how many horses are in this image?" and "how many horses can you see in this image?". They have the same meaning, essentially captured by the first three words. A machine that attends to the first three words would arguably be more robust to linguistic variations irrelevant to the meaning and answer of the question. Motivated by this observation, in addition to reasoning about visual attention, authors also address the problem of question attention.
Main Contributions
- A novel co-attention mechanism for VQA that jointly performs question-guided visual attention and image-guided question attention.
- A hierarchical architecture to represent the question, and consequently construct image-question co-attention maps at 3 different levels: word level, phrase level and question level.
- A novel convolution-pooling strategy at phase-level to adaptively select the phrase sizes whose representations are passed to the question level representation.
- Results on VQA and COCO-QA and ablation studies to quantify the roles of different components in our model
Method
This section is broken down into three parts: (i) notations used within the paper, (ii) hierarchical representation of the visual question and (iii) the proposed co-attention mechanism.
Notations
| Notation | Explaination |
| $Q = \{q_1,...q_T\}$ | One-hot encoding of a visual question with $T$ words. Paper uses three different representation og visual question, one for each level of hierarchy, they are as follows:
$Q^{w,p,s}$ has exactly $T$ number of embeddings in it, regardless of its position in the hierarchy i.e. word, phrase or question. |
| $V = {v_1,..,v_N}$ | $V$ represented various feature vectors from $N$ different locations within the given image. Therefore, $v_n$ is feature vector from the image at location $n$. One can extract these location sensitive features from convolution layer of CNN. |
| $\hat{v}^r$ and $\hat{q}^r$ | The co-attention features of image and question at each level in the hierarchy where $r \in \{w,p,s\}$. Basically, its a sum of $Q$ or $V$ after the dot product with attention $a^q$ or $a^v$ at each level of hierarchy.
For example, at word level, $a^q$ and $a^v$ tell importance of each words in visual question and each locations within image respectively, whereas $\hat{q}^w$ and $\hat{v}^w$ are final features vectors representing question and image with attention map applied at word level. |
Note: Throughout the paper, $W$ represents the learnable weights and biases are not used within the equations for simplicity (reader must assume it to exist).
Question Hierarchy
There are three levels of hierarchy to represent a visual question: (i) word, (ii) phrase and (iii) question level as discussed in follwing sub-sections. It is important of note, each level of hierarchy depends on the previous one, so, phrase level representations are extracted from word level and question level representation comes from phrase level as depicted in Figure 4 and dicussed further in following sub-sections.
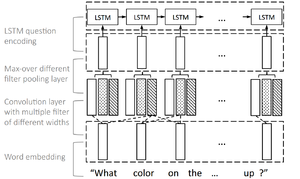
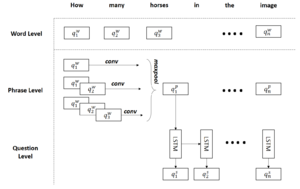
Word Level
1-hot encoding of question's words $Q = \{q_1,..q_T\}$ are transformed into vector space (learned end-to-end) which represents word level embedding of the visual question i.e. $Q^w = \{q^w_1,...q^w_T\}$. This transformation can be learn end-to-end instead of some pretrained word2vec model.
Phrase Level
Phrase level embedding vectors are calculated by using 1-D convolutions on the word level embedding vectors. Concretely, at each word location, we compute the inner product of the word vectors with filters of three window sizes: unigram, bigram and trigram as illustrated by Figure 4. For the t-th word, the convolution output with window size s is given by
$$ \hat{q}^p_{s,t} = tanh(W_c^sq^w_{t:t+s-1}), \quad s \in \{1,2,3\} $$
Where $W_c^s$ is the weight parameters. These diferent n-grams features are combined together using maxpool operator to obtain phrase-level features.
$$ q_t^p = max(\hat{q}^p_{1,t}, \hat{q}^p_{2,t}, \hat{q}^p_{3,t}), \quad t \in \{1,2,...,T\} $$
Question Level
For question level representation, LSTM is used to encode the sequence $q_t^p$ after max-pooling. The corresponding question-level feature at time t $q_t^s$ is the LSTM hidden vector at time t $h_t$.
$$ \begin{align*} h_t &= LSTM(q_t^p, h_{t-1})\\ q_t^s &= h_t \end{align*} $$
Co-attention Mechanism
Paper has proposed two co-attention mechanisms.
| Parallel co-attention | Generates image and question attention simultaneously. |
| Alternating co-attention | Sequentially alternates between generating image and question attentions. |
These co-attention mechanisms are executed at all three levels of the question hierarchy yielding $\hat{v}^r$ and $\hat{q}^r$ where $r$ is levels in hierarchy i.e. $r \in \{w,p,s\}$ (refer to Notations section). Following sub-sections explains both the co-attention mehcnaism throughly.
Parallel Co-Attention
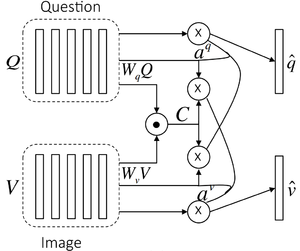
Parallel co-attention attends to the image and question simultaneously as shown in Figure 5. In the paper, "affinity matrix" has been mentioned as the way to calculate the "attention" or affinity for every pair of image location and question part for each level in the hierarchy (word, phrase and question). Remember, there are $N$ image locations and $T$ question parts, thus affinity matrix is $R^{T \times N}$. Specifically, for a given image with feature map $V \in R^{d \times N}$, and the question representation $Q \in R^{d \times T}$, the affinity matrix $C \in R^{T \times N}$ is calculated by
$$ C = tanh(Q^TW_bV) $$
where $W_b \in R^{d \times d}$ contains the weights. After computing this affinity matrix, one possible way of computing the image (or question) attention is to simply maximize out the affinity over the locations of other modality, i.e. $a_v[n] = maxi(C_{i,n})$ and $a_q[t] = maxj(C_{t,j})$. Instead of choosing the max activation, paper has considered the affinity matrix as a feature and learn to predict image and question attention maps via the following
$$ H_v = tanh(W_vV + (W_qQ)C), \quad H_q = tanh(W_qQ + (W_vV )C^T )\\ a_v = softmax(w_{hv}^T Hv), \quad aq = softmax(w_{hq}^T H_q) $$
where $W_v, W_q \in R^{k \times d}$, $w_{hv}, w_{hq} \in R^k$ are the weight parameters. $a_v \in R^N$ and $a_q \in R^T$ are the attention probabilities of each image region $v_n$ and word $q_t$ respectively. The affinity matrix $C$ transforms question attention space to image attention space (vice versa for $C^T$). Based on the above attention weights, the image and question attention vectors are calculated as the weighted sum of the image features and question features, i.e.,
$$\hat{v} = \sum_{n=1}^{N}{a_n^v v_n}, \quad \hat{q}\sum_{t=1}^{T}{a_t^q q_t}$$
The parallel co-attention is done at each level in the hierarchy, leading to $\hat{v}^r$ and $\hat{q}^r$ where $r \in \{w,p,s\}$.
Alternating Co-Attention
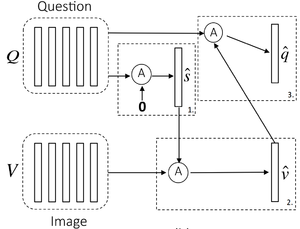
In this attention mechanism, authors sequentially alternate between generating image and question attention as shown in Figure 6, however read further to understand that figure. Briefly, this consists of three steps
- Summarize the question into a single vector $q$
- Attend to the image based on the question summary $q$
- Attend to the question based on the attended image feature.
Concretely, paper defines an attention operation $\hat{x} = A(X, g)$, which takes the image (or question) features $X$ and attention guidance $g$ derived from question (or image) as inputs, and outputs the attended image (or question) vector. The operation can be expressed in the following steps
$$ \begin{align*} H &= tanh(W_xX + (W_gg)1^T)\\ a_x &= softmax(w_{hx}^T H)\\ \hat{x} &= \sum{a_i^x x_i} \end{align*} $$
where $1$ is a vector with all elements to be 1. $W_x, W_g \in R^{k\times d}$ and $w_{hx} \in R^k$ are parameters. $a_x$ is the attention weight of feature $X$.
- At the first step of alternating coattention, $X = Q$, and $g$ is $0$.
- At the second step, $X = V$ where $V$ is the image features, and the guidance $g$ is intermediate attended question feature $\hat{s}$ from the first step
- Finally, we use the attended image feature $\hat{v}$ as the guidance to attend the question again, i.e., $X = Q$ and $g = \hat{v}$.
Similar to the parallel co-attention, the alternating co-attention is also done at each level of the hierarchy, leading to $\hat{v}^r$
and $\hat{q}^r$ where $r \in \{w,p,s\}$.