Graph Structure of Neural Networks: Difference between revisions
| Line 23: | Line 23: | ||
= Discussions and Conclusions = | = Discussions and Conclusions = | ||
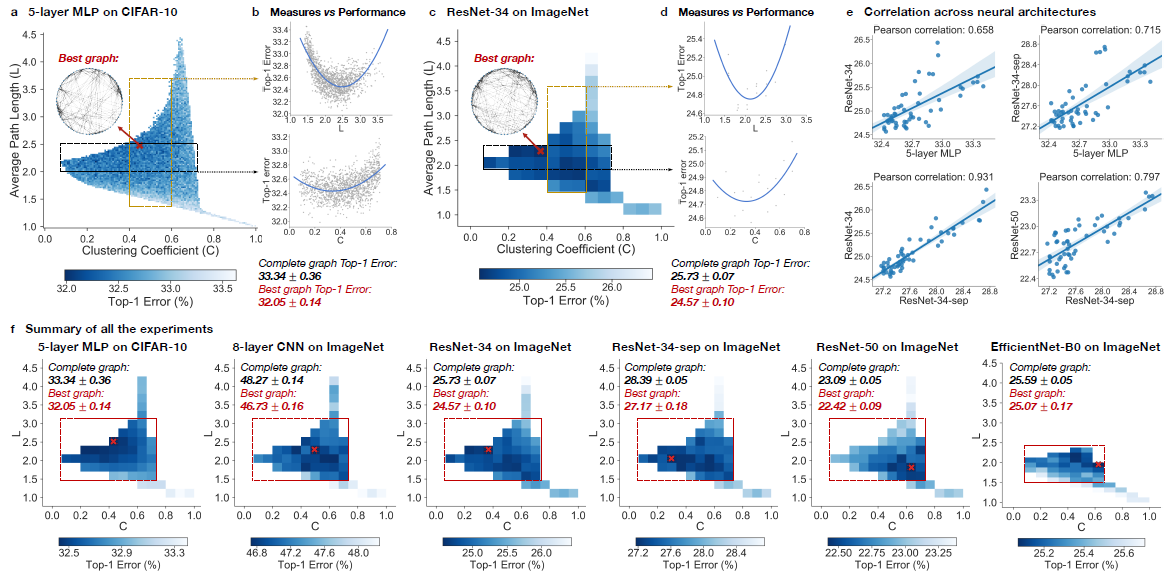
Section 5 of the paper summarize the result of experiment among multiple different relational graphs through sampling and analyzing. | |||
[[File:Result2_441_2020Group16.png]] | [[File:Result2_441_2020Group16.png]] | ||
== 1. Neural networks performance depends on its structure == | == 1. Neural networks performance depends on its structure == | ||
In the experiment, top-1 errors are going to be used to measure the performance of the model. The parameters of the models are average path length and clustering coefficient. Heat maps was created to illustrate the difference of predictive performance among possible average path length and clustering coefficient. In Figure ???, The darker area represents a smaller top-1 error which indicate the model perform better than other area. | |||
Compare with the complete graph which has A = 1 and C = 1, The best performing relational graph can outperform the complete graph baseline by 1.4% top-1 error for MLP on CIFAR-10, and 0.5% to 1.2% for models on ImageNet. Hence it is an indicator that the predictive performance of neural network highly depends on the graph structure, or equivalently that completed graph does not always preform the best. | |||
the complete graph | |||
The best performing relational graph can outperform the | |||
complete graph baseline by 1.4% top-1 error for MLP on | |||
CIFAR-10, and 0.5% to 1.2% for models on ImageNet. | |||
== 2. Sweet spot where performance is significantly improved == | == 2. Sweet spot where performance is significantly improved == | ||
To | To reduce the training noise, the 3942 graphs that in the sample had been grouped into 52 bin, each bin had been colored based on the average performance of graphs that fall into the bin. Based on the heat map, the well-performing graphs tend to cluster into a special spot that the paper called “sweet spot” shown in the red rectangle. | ||
average performance of graphs that fall into the bin | |||
map, | |||
into a “sweet spot” | |||
== 3. Relationship between neural network’s performance and parameters == | == 3. Relationship between neural network’s performance and parameters == | ||
When we visualize the heat map, we can see that there are no significant jump of performance that occurred as small change of clustering coefficient and average path length. If one of the variable is fixed in a small range, it is observed that a second degree polynomial is a good visualization tools for the overall trend. Therefore, both clustering coefficient and average path length are highly related with neural network performance by a U-shape. | |||
performance | |||
U-shape | |||
== 4. Consistency among many different tasks and datasets == | == 4. Consistency among many different tasks and datasets == | ||
It is observed that the results are consistent through different point of view. Among multiple architecture dataset, it is observed that the clustering coefficient within [0.1,0.7] and average path length with in [1.5,3] consistently outperform the baseline complete graph. | |||
Among different dataset with network that has similar clustering coefficient and average path length, the results are correlated, The paper mentioned that ResNet-34 is much more complex than 5-layer MLP but a fixed set relational graphs would perform similarly in both setting, with Pearson correlation of 0.658, the p-value for the Null hypothesis is less than 10^-8. | |||
and average path length | |||
network | |||
MLP | |||
similarly in both | |||
of 0.658 | |||
== 5. top architectures can be identified efficiently == | == 5. top architectures can be identified efficiently == | ||
Revision as of 15:26, 15 November 2020
Presented By
Xiaolan Xu, Robin Wen, Yue Weng, Beizhen Chang
Introduction
We develop a new way of representing a neural network as a graph, which we call relational graph. Our key insight is to focus on message exchange, rather than just on directed data flow. As a simple example, for a fixedwidth fully-connected layer, we can represent one input channel and one output channel together as a single node, and an edge in the relational graph represents the message exchange between the two nodes (Figure 1(a)).
Relational Graph
Parameter Definition
(1) Clustering Coefficient
(2) Average Path Length
Experimental Setup (Section 4 in the paper)
Discussions and Conclusions
Section 5 of the paper summarize the result of experiment among multiple different relational graphs through sampling and analyzing.
1. Neural networks performance depends on its structure
In the experiment, top-1 errors are going to be used to measure the performance of the model. The parameters of the models are average path length and clustering coefficient. Heat maps was created to illustrate the difference of predictive performance among possible average path length and clustering coefficient. In Figure ???, The darker area represents a smaller top-1 error which indicate the model perform better than other area. Compare with the complete graph which has A = 1 and C = 1, The best performing relational graph can outperform the complete graph baseline by 1.4% top-1 error for MLP on CIFAR-10, and 0.5% to 1.2% for models on ImageNet. Hence it is an indicator that the predictive performance of neural network highly depends on the graph structure, or equivalently that completed graph does not always preform the best.
2. Sweet spot where performance is significantly improved
To reduce the training noise, the 3942 graphs that in the sample had been grouped into 52 bin, each bin had been colored based on the average performance of graphs that fall into the bin. Based on the heat map, the well-performing graphs tend to cluster into a special spot that the paper called “sweet spot” shown in the red rectangle.
3. Relationship between neural network’s performance and parameters
When we visualize the heat map, we can see that there are no significant jump of performance that occurred as small change of clustering coefficient and average path length. If one of the variable is fixed in a small range, it is observed that a second degree polynomial is a good visualization tools for the overall trend. Therefore, both clustering coefficient and average path length are highly related with neural network performance by a U-shape.
4. Consistency among many different tasks and datasets
It is observed that the results are consistent through different point of view. Among multiple architecture dataset, it is observed that the clustering coefficient within [0.1,0.7] and average path length with in [1.5,3] consistently outperform the baseline complete graph.
Among different dataset with network that has similar clustering coefficient and average path length, the results are correlated, The paper mentioned that ResNet-34 is much more complex than 5-layer MLP but a fixed set relational graphs would perform similarly in both setting, with Pearson correlation of 0.658, the p-value for the Null hypothesis is less than 10^-8.