Graph Structure of Neural Networks: Difference between revisions
| Line 24: | Line 24: | ||
where <math>\mathbf{x}^{(r+1)}</math> is the feature of of the <math>v</math> node in the relational graph after the <math>r^{th}</math> round of update. <math>u,v</math> are nodes in Graph <math>G</math>. <math>N(u)=\{u|(u,v)\in E\}</math> is the set of all the neighbor nodes of <math>u</math> in graph <math>G</math>. | where <math>\mathbf{x}^{(r+1)}</math> is the feature of of the <math>v</math> node in the relational graph after the <math>r^{th}</math> round of update. <math>u,v</math> are nodes in Graph <math>G</math>. <math>N(u)=\{u|(u,v)\in E\}</math> is the set of all the neighbor nodes of <math>u</math> in graph <math>G</math>. | ||
To further illustrate the above, we use the basic Multilayer Perceptron (MLP) as an example. A MLP consists of layers of neurons, where each neuron performs | To further illustrate the above, we use the basic Multilayer Perceptron (MLP) as an example. A MLP consists of layers of neurons, where each neuron performs a weighted sum over scalar inputs and outputs, followed by some non-linearity. Suppose the <math>r^{th}</math> layer of an MLP takes <math>x^{(r)}</math> as input and <math>x^{(r+1)}</math> as output, then a neuron computes | ||
<div style="text-align:center;"><math>x_i^{(r+1)}= \sigma(\Sigma_jw_{ij}^{(r)}x_j^{(r)})</math>.</div> | <div style="text-align:center;"><math>x_i^{(r+1)}= \sigma(\Sigma_jw_{ij}^{(r)}x_j^{(r)})</math>.</div> | ||
Revision as of 14:50, 17 November 2020
Presented By
Xiaolan Xu, Robin Wen, Yue Weng, Beizhen Chang
Introduction
During the study of Neural Networks, it is especially important to build a relation between a neural network’s accuracy and its underlying graph structure. The natural choice is to use computational graph representation but it has many limitations such as lack of generality and disconnection with biology/neuroscience.
Thus, we develop a new way of representing a neural network as a graph, which we call a relational graph. Our key insight is to focus on message exchange, rather than just on directed data flow. For example, for a fixed-width fully-connected layer, we can represent one input channel and one output channel together as a single node, and an edge in the relational graph represents the message exchange between the two nodes. Under this formulation, using the appropriate message exchange definition, we show that the relational graph can represent many types of neural network layers.
We designed WS-flex, as a graph generator that allows us to systematically explore the design space of neural networks. We characterize neural networks by the clustering coefficient and average path length of their relational graphs under the insights of neuroscience.
Neural Network as Relational Graph
The author proposes the concept of relational graph to study the graphical structure of neural network. Each relational graph is based on an undirected graph [math]\displaystyle{ G =(V; E) }[/math], where [math]\displaystyle{ V =\{v_1,...,v_n\} }[/math] is the set of all the nodes, and [math]\displaystyle{ E \subseteq \{(v_i,v_j)|v_i,v_j\in V\} }[/math] is the set of all edges that connect nodes. Note that for the graph used here, all nodes have self edges, that is [math]\displaystyle{ (v_i,v_i)\in E }[/math].
To build a relational graph that captures the message exchange between neurons in the network, we associate various mathematical quantities to the graph [math]\displaystyle{ G }[/math]. First, a feature quantity [math]\displaystyle{ x_v }[/math] is associated with each node. The quantity [math]\displaystyle{ x_v }[/math] might be a scalar, vector or tensor depending on different types of neural networks (see the Table at the end of the section). Then a message function [math]\displaystyle{ f_{uv}(·) }[/math] is associated with every edge in the graph. A message function specifically takes a node’s feature as the input and then output a message. An aggregation function [math]\displaystyle{ {\rm AGG}_v(·) }[/math] then takes a set of messages (the outputs of message function) and outputs the updated node feature.
A relation graph is a graph [math]\displaystyle{ G }[/math] associated with several rounds of message exchange, which transfrom the fearure quantity [math]\displaystyle{ x_v }[/math] with the message function [math]\displaystyle{ f_{uv}(·) }[/math] and the aggregation function [math]\displaystyle{ {\rm AGG}_v(·) }[/math]. At each round of message exchange, each node sends messages to its neighbors and aggregates incoming messages from its neighbors. Each message is transformed at each edge through the message function, then they are aggregated at each node via the aggregation function. Suppose we have already conducted [math]\displaystyle{ r-1 }[/math] rounds of message exchange, then the [math]\displaystyle{ r^{th} }[/math] round of message exchange for a node [math]\displaystyle{ v }[/math] can be described as
where [math]\displaystyle{ \mathbf{x}^{(r+1)} }[/math] is the feature of of the [math]\displaystyle{ v }[/math] node in the relational graph after the [math]\displaystyle{ r^{th} }[/math] round of update. [math]\displaystyle{ u,v }[/math] are nodes in Graph [math]\displaystyle{ G }[/math]. [math]\displaystyle{ N(u)=\{u|(u,v)\in E\} }[/math] is the set of all the neighbor nodes of [math]\displaystyle{ u }[/math] in graph [math]\displaystyle{ G }[/math].
To further illustrate the above, we use the basic Multilayer Perceptron (MLP) as an example. A MLP consists of layers of neurons, where each neuron performs a weighted sum over scalar inputs and outputs, followed by some non-linearity. Suppose the [math]\displaystyle{ r^{th} }[/math] layer of an MLP takes [math]\displaystyle{ x^{(r)} }[/math] as input and [math]\displaystyle{ x^{(r+1)} }[/math] as output, then a neuron computes
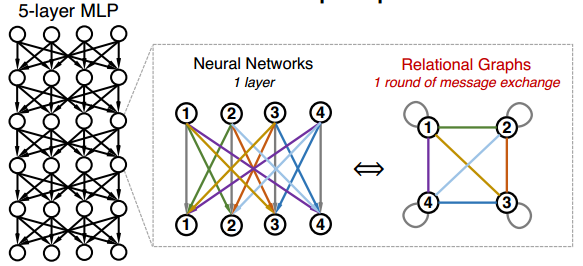
where [math]\displaystyle{ w_{ij}^{(r)} }[/math] is the trainable weight and [math]\displaystyle{ \sigma }[/math] is the non-linearity function. Let's first consider the special case where the input and output of all the layers [math]\displaystyle{ x^{(r)}, 1 \leq r \leq R }[/math] have the same feature dimensions $d$. In this scenario, we can have $d$ nodes in the Graph $G$ with each node representing a neuron in MLP. Each layer of neural network will correspond with a round of message exchange, so there will be $R$ rounds of message exchange in total. The aggregation function here will be the summation with non-linearity transform [math]\displaystyle{ \sigma(\Sigma) }[/math], while the message function is simply the scalar multipication with weight. A fully-connected, fixed-width MLP layer can then be expressed with a complete relational graph, where each node $x_v$ connects to all the other nodes in F, that is neighborhood set [math]\displaystyle{ N(v) = V }[/math] for each node [math]\displaystyle{ v }[/math]. The table below shows the correspondence between the complete relation graph with a 5-layer 4-dimension fully-connected MLP.
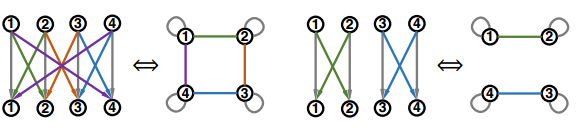
In fact, a fixed-width fully-connected MLP is only a special case under a much more general model family, where the message function, aggregation function, and most importantly, the relation graph structure can vary. The different relational graph will represent the different topological structure and information exchange pattern of the network, which is the property that the paper wants to examine. The plot below shows two examples of non-fully connected fixed-width MLP and their corresponding relational graphs.
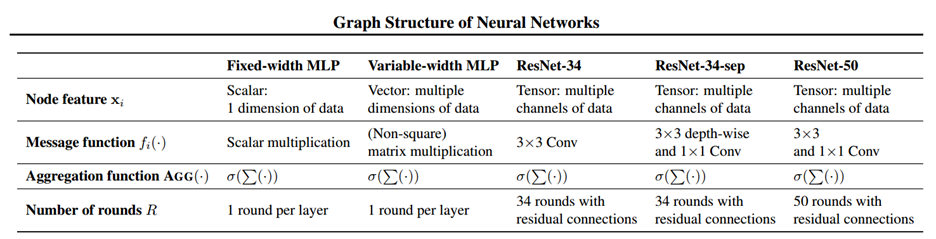
We can generalize the above definitions for fixed-with MLP to Variable-width MLP, Convolutinal Neural Network (CNN) and other modern network architecture like Resnet by allowing the node feature quantity $\textbf{x}_j^{(r)}$ to be a vector or tensor respectively. In this case, each node in the relational graph will represent multiple neurons in the network. The messega function will then change from the simple scalar multiplication to either matrix/tensor multiplication or convolution. The detailed representation of these more complicated networks are given in the paper. The correspondence between different networks and their relational graph properties is summarized in the table below.
Overall, relational graphs provide a general representation for neural networks. With proper definitions of node features and message exchange, relational graphs can represent diverse neural architectures, thereby allowing us to study the graph structure of neural networks.
Exploring and Generating Relational Graphs
We will deal with the design and how to explore the space of relational graphs in this section. There are three parts we need to consider:
(1) Graph measures that characterize graph structural properties:
We will use one global graph measure, average path length, and one local graph measure, clustering coefficient in this paper. To explain clearly, average path length measures the average shortest path distance between any pair of nodes; the clustering coefficient measures the proportion of edges between the nodes within a given node’s neighbourhood, divided by the number of edges that could possibly exist between them, averaged over all the nodes.
(2) Graph generators that can generate the diverse graph:
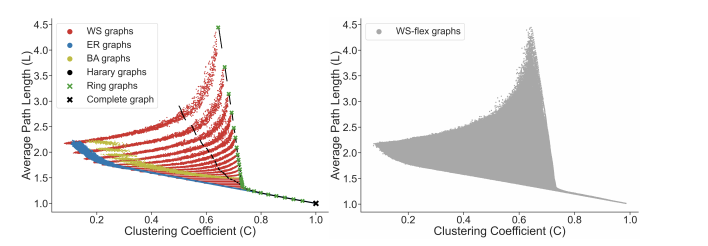
With selected graph measures, we use a graph generator to generate diverse graphs to cover a large span of graph measures. To figure out the limitation of the graph generator and find out the best, we investigate some generators including ER, WS, BA, Harary, Ring, Complete graph and results shows as below:
Thus, from the picture, we could obtain the WS-flex graph generator that can generate graphs with a wide coverage of graph measures; notably, WS-flex graphs almost encompass all the graphs generated by classic random generators mentioned above.
(3) Computational Budget that we need to control so that the differences in performance of different neural networks are due to their diverse relational graph structures.
It is important to ensure that all networks have approximately the same complexities so that the differences in performance are due to their relational graph structures when comparing neutral work by their diverse graph.
We use FLOPS (# of multiply-adds) as the metric. We first compute the FLOPS of our baseline network instantiations (i.e. complete relational graph) and use them as the reference complexity in each experiment. From the description in section 2, a relational graph structure can be instantiated as a neural network with variable width. Therefore, we can adjust the width of a neural network to match the reference complexity without changing the relational graph structures.
Experimental Setup
CIFAR-10 dataset: 10 classes, 50K training images and 10K validation images
ImageNet classification: 1K image classes, 1.28M training images and 50K validation images.
Discussions and Conclusions
The paper summarizes the result of experiment among multiple different relational graphs through sampling and analyzing and list six important observations during the experiments, These are:
- There are always exists graph structure that has higher predictive accuracy under Top-1 error compare to the complete graph
- There is a sweet spot that the graph structure near the sweet spot usually outperform the base graph
- The predictive accuracy under top-1 error can be represented by a smooth function of Average Path Length [math]\displaystyle{ (L) }[/math] and Clustering Coefficient [math]\displaystyle{ (C) }[/math]
- The Experiments is consistent across multiple dataset and multiple graph structure with similar Average Path Length and Clustering Coefficient.
- The best graph structure can be identified easily.
- There is similarity between best artificial neurons and biological neurons.
$$\text{Figure - Results from Experiments}$$
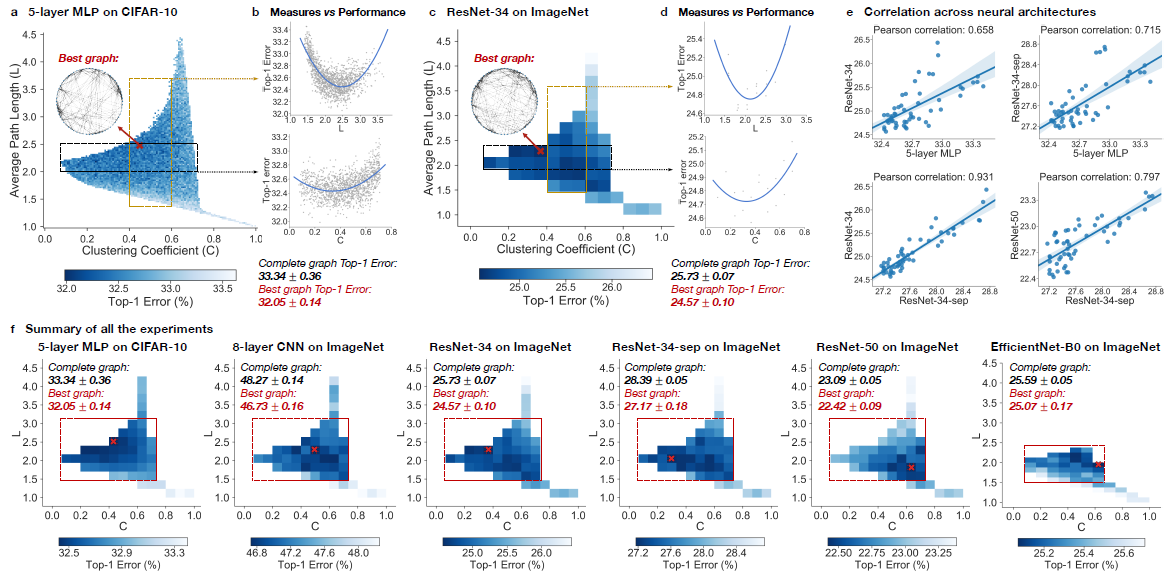
Neural networks performance depends on its structure
During the experiment, Top-1 errors for all sampled relational graph among multiple tasks and graph structures are recorded. The parameters of the models are average path length and clustering coefficient. Heat maps was created to illustrate the difference of predictive performance among possible average path length and clustering coefficient. In Figure - Results from Experiments (a)(c)(f), The darker area represents a smaller top-1 error which indicate the model perform better than light area.
Compare with the complete graph which has parameter [math]\displaystyle{ L = 1 }[/math] and [math]\displaystyle{ C = 1 }[/math], The best performing relational graph can outperform the complete graph baseline by 1.4% top-1 error for MLP on CIFAR-10, and 0.5% to 1.2% for models on ImageNet. Hence it is an indicator that the predictive performance of neural network highly depends on the graph structure, or equivalently that completed graph does not always has the best performance.
Sweet spot where performance is significantly improved
It had been recognized that training noises often results in inconsistent predictive results. In the paper, the 3942 graphs that in the sample had been grouped into 52 bin, each bin had been colored based on the average performance of graphs that fall into the bin. By taking the average, the training noises had been significantly reduced. Based on the heat map Figure - Results from Experiments (f), the well-performing graphs tend to cluster into a special spot that the paper called “sweet spot” shown in the red rectangle, the rectangle is approximately included clustering coefficient in the range [math]\displaystyle{ [0.1,0.7] }[/math] and average path length with in [math]\displaystyle{ [1.5,3] }[/math].
Relationship between neural network’s performance and parameters
When we visualize the heat map, we can see that there are no significant jump of performance that occurred as small change of clustering coefficient and average path length (Figure - Results from Experiments (a)(c)(f)). In addition, if one of the variable is fixed in a small range, it is observed that a second degree polynomial is a good visualization tools for the overall trend (Figure - Results from Experiments (b)(d)). Therefore, both clustering coefficient and average path length are highly related with neural network performance by a U-shape.
Consistency among many different tasks and datasets
The paper present consistency use two perspective, one is qualitative consistency and another one is quantitative consistency.
(1) Qualitative Consistency It is observed that the results are consistent through different point of view. Among multiple architecture dataset, it is observed that the clustering coefficient within [math]\displaystyle{ [0.1,0.7] }[/math] and average path length with in [math]\displaystyle{ [1.5,3] }[/math] consistently outperform the baseline complete graph.
(2) Quantitative Consistency Among different dataset with network that has similar clustering coefficient and average path length, the results are correlated, The paper mentioned that ResNet-34 is much more complex than 5-layer MLP but a fixed set relational graphs would perform similarly in both setting, with Pearson correlation of [math]\displaystyle{ 0.658 }[/math], the p-value for the Null hypothesis is less than [math]\displaystyle{ 10^{-8} }[/math].
top architectures can be identified efficiently
According to the graphs we have in the Key Results. We can see that there is a "sweet spot" and therefore, we do not have to train the entire data set for a large value of epoch or a really large sample. We can take a sample of the data around 52 graphs that would have a correlation of 0.9 which indicates that fewer samples are needed for a similar analysis in practice. Within 3 epochs, the correlation between the variables is already high enough for future computation.
well-performing neural networks have graph structure surprisingly similar to those of real biological neural networks
The way we define relational graphs and average length in the graph is similar to the way information is exchanged in network science. The biological neural network also has a similar relational graph representation and graph measure with the best-performing relational graph.
Critique
1. The experiment is only measuring on a single data set which might impact the conclusion since this is not representative enough. 2. When we are fitting the model, training data should be randomized in each epoch to reduce the noise.