GradientLess Descent: Difference between revisions
| Line 53: | Line 53: | ||
Curiously, a large amount of this approach focuses on approximating gradients and then using first-order optimisation algorithms. | Curiously, a large amount of this approach focuses on approximating gradients and then using first-order optimisation algorithms. | ||
This paper presents a purely gradientless algorithm, proposes a geometric approach to analyse the algorithm, and proves a <math display="inline">O( k Q \log (n / \epsilon ))</math> convergence bound. | This paper presents a purely gradientless algorithm, proposes a geometric approach to analyse the algorithm, and proves a <math display="inline">O( k Q \log (n / \epsilon ))</math> convergence bound. Here the latent dimension is <math display="inline"> k </math> and <math display="inline"> k < n </math>, where <math display="inline"> n </math> is the input dimension. | ||
==GradientLess Descent Algorithm== | ==GradientLess Descent Algorithm== | ||
Revision as of 18:35, 2 November 2020
Introduction
In this presentation, we are interested in minimising a smooth convex function without ever computing its derivatives.
Motivation and Set-up
A general optimisation question can be formulated by asking to minimise an objective function [math]\displaystyle{ f : \mathbb{R}^n \to \mathbb{R} }[/math], which means finding: \begin{align*} x^* = \mathrm{argmin}_{x \in \mathbb{R}^n} f(x) \end{align*}
Depending on the nature of [math]\displaystyle{ f }[/math], different settings may be considered:
- Convex vs non-convex objective functions;
- Differentiable vs non-differentiable objective functions;
- Allowed function or gradient computations;
- Noisy/Stochastic oracle access.
For the purpose of this paper, we consider convex smooth objective noiseless functions, where we have access to function computations but not gradient computations. This class of functions is quite common in practice; for instance, they make special appearances in the reinforcement learning literature.
To be even more precise, in our context we let [math]\displaystyle{ K \subseteq \mathbb{R}^n }[/math] be compact [math]\displaystyle{ f : K \to \mathbb{R} }[/math] be [math]\displaystyle{ \beta }[/math]-smooth and [math]\displaystyle{ \alpha }[/math]-strongly convex.
Definition 1
A convex continuously differentiable function [math]\displaystyle{ f : K \to \mathbb{R} }[/math] is [math]\displaystyle{ \alpha }[/math]-strongly convex for [math]\displaystyle{ \alpha \gt 0 }[/math] if \begin{align*} f(y) \geq f(x) + \left\langle \nabla f(x), y-x\right\rangle + \frac{\alpha}{2} ||y - x||^2 \end{align*} [math]\displaystyle{ \forall x,y \in K }[/math]. It is called [math]\displaystyle{ \beta }[/math]-smooth for [math]\displaystyle{ \beta \gt 0 }[/math] if \begin{align*} f(y) \leq f(x) + \left\langle \nabla f(x), y-x\right\rangle + \frac{\beta}{2} || y - x||^2 \end{align*} [math]\displaystyle{ \forall x,y \in K }[/math]
We remark that if [math]\displaystyle{ f }[/math] is twice continuously differentiable, this is simply equivalent to the eigenvalues of the Hessian matrix [math]\displaystyle{ \textbf{H}f }[/math] being bounded between [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math]. Further intuition can be gained from the image below, showing how such a function can be contained within quadratic bounds.
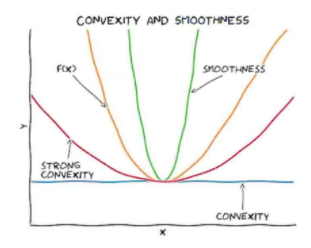
In convex analysis, one usually says that a function has condition number [math]\displaystyle{ Q }[/math] if it is both [math]\displaystyle{ \alpha }[/math]-strongly convex, and [math]\displaystyle{ \beta }[/math]-smooth, and [math]\displaystyle{ \frac{\beta}{\alpha} \leq Q }[/math]. The authors of this paper consider the more general case where [math]\displaystyle{ f }[/math] is a monotone transformation of a [math]\displaystyle{ \alpha }[/math]-strongly convex and [math]\displaystyle{ \beta }[/math]-smooth function; for simplicity and transparency, we shall not consider these extensions here, but shall note that their proofs are quite elementary.
Zeroth-Order Optimisation
In zeroth-order optimisation, we are interested in minimising a function without computing its derivatives. This is important in many practical applications in which derivatives may not be available or they may be difficult to compute, such as:
- Combinatorial (i.e. discrete) optimisation
- Instances of non-analytic loss functions (e.g. hyperparameter tuning)
- Adversarial attacks
- Reinforcement learning
Curiously, a large amount of this approach focuses on approximating gradients and then using first-order optimisation algorithms.
This paper presents a purely gradientless algorithm, proposes a geometric approach to analyse the algorithm, and proves a [math]\displaystyle{ O( k Q \log (n / \epsilon )) }[/math] convergence bound. Here the latent dimension is [math]\displaystyle{ k }[/math] and [math]\displaystyle{ k \lt n }[/math], where [math]\displaystyle{ n }[/math] is the input dimension.
GradientLess Descent Algorithm
The proposed algorithm is given in the picture below.

Observe that at each step, we perform binary search over several concentric circles and randomly sample points, in the hopes that if we take a small step in a random direction this will reduce the value of the objective function.
Proof of correctness
The correctness of this algorithm hinges on two observations. The first one is about the volume of the intersection of high-dimensional balls; we call this intersection a hyperspherical cap.
Theorem 1
Let [math]\displaystyle{ B_1, B_2 \subseteq \mathbb{R}^n }[/math] be balls of radii [math]\displaystyle{ r_1, r_2 }[/math]. Let [math]\displaystyle{ \ell }[/math] be the distance between the centres. If [math]\displaystyle{ r_1 \in \left[ \frac{\ell}{2 \sqrt{n}} , \frac{\ell}{\sqrt{n}} \right] }[/math] and [math]\displaystyle{ r_2 \geq \ell - \frac{\ell}{4n} }[/math], then [math]\displaystyle{ \lambda (B_1 \cap B_2) \geq c_n \lambda (B_1) }[/math], where [math]\displaystyle{ c_n \geq \frac{1}{4} }[/math].
Using this theorem about random searches in high dimensions, we can prove the correctness of our algorithm.
Theorem 2
For any [math]\displaystyle{ x \in K }[/math] such that [math]\displaystyle{ \frac{3}{5Q} ||x - x^*|| \in [C_1, C_2] }[/math], we can find integers [math]\displaystyle{ 0 \leq k_1, k_2 \lt \log \frac{C_2}{C_1} }[/math] such that if [math]\displaystyle{ r = 2^{k_1}C_1 }[/math] or [math]\displaystyle{ r = 2^{-k_2}C_2 }[/math], then a sample [math]\displaystyle{ y }[/math] from the uniform distribution on [math]\displaystyle{ B_x = B\left( x, \frac{r}{\sqrt{n}} \right) }[/math] satisfies \begin{align*} f(y) - f(x^*) \leq (f(x) - f(x^*)) \left( 1- \frac{1}{5nQ} \right) \end{align*} with probability at least [math]\displaystyle{ \frac{1}{4} }[/math].
Notice how the second theorem implies that with probability a quarter, [math]\displaystyle{ f(y) }[/math] is closer to the optimum than [math]\displaystyle{ f(x) }[/math] is.
For proofs of these theorems, please watch my talk.
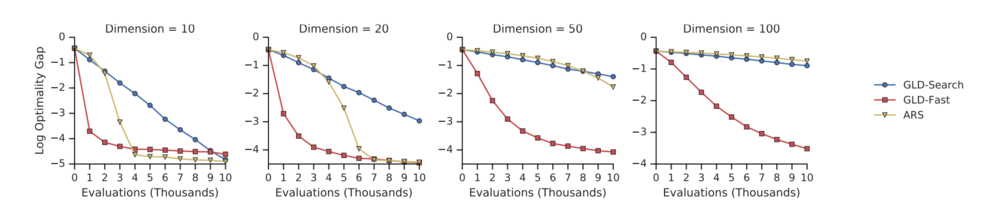
Results
We compare the GradientLess Descent algorithm to a benchmark established by the Augmented Randomised Search algorithm proposed in 2011.
For this comparison, we defined the function [math]\displaystyle{ f(x) = \frac{1}{2} x^T H x }[/math] where [math]\displaystyle{ H }[/math] is a diagonal matrix with eigenvalues linearly interpolating the interval [math]\displaystyle{ [\alpha , \beta] }[/math]. We observe that in most scenarios, GradientLess Descent beats the benchmark.