Fix your classifier: the marginal value of training the last weight layer: Difference between revisions
No edit summary |
No edit summary |
||
| Line 105: | Line 105: | ||
The authors have evaluated their proposed model on the following datasets: | The authors have evaluated their proposed model on the following datasets: | ||
== | ==CIFAR-10/100== | ||
===About the dataset=== | ===About the dataset=== | ||
| Line 116: | Line 116: | ||
<center>[[File: figure1_resnet_cifar10.png]]</center> | <center>[[File: figure1_resnet_cifar10.png]]</center> | ||
These results demonstrate that although the training error is considerably lower for the network with learned classifier, both models achieve the same classification accuracy on the validation set. The authors conjecture is that with the new fixed parameterization, the network can no longer increase the | |||
norm of a given sample’s representation - thus learning its label requires more effort. As this may happen for specific seen samples - it affects only training error. | |||
The authors also compared using a fixed scale variable <math>\alpha </math> at different values vs. the learned parameter. Results for <math> \alpha = </math> {0.1, 1, 10} are depicted in [[Media: figure_3_link.png| Figure 3]] for both training and validation error. | |||
Revision as of 13:39, 27 November 2018
Introduction
Deep neural networks have become a widely used model for machine learning, achieving state-of-the-art results on many tasks. The most common task these models are used for is to perform classification, as in the case of convolutional neural networks (CNNs) used to classify images to a semantic category. Typically, a learned affine transformation is placed at the end of such models, yielding a per-class value used for classification. This classifier can have a vast number of parameters, which grows linearly with the number of possible classes, thus requiring increasingly more computational resources.
Brief Overview
In order to alleviate the aforementioned problem, the authors propose that the final layer of the classifier be fixed (upto a global scale constant). They argue that with little or no loss of accuracy for most classification tasks, the method provides significant memory and computational benefits. In addition, they show that by initializing the classifier with a Hadamard matrix the inference could be made faster as well.
Previous Work
Training NN models and using them for inference requires large amounts of memory and computational resources; thus, extensive amount of research has been done lately to reduce the size of networks which are as follows:
- Weight sharing and specification (Han et al., 2015)
- Mixed precision to reduce the size of the neural networks by half (Micikevicius et al., 2017)
- Low-rank approximations to speed up CNN (Tai et al., 2015)
- Quantization of weights, activations and gradients to further reduce computation during training (Hubara et al., 2016b; Li et al., 2016 and Zhou et al., 2016)
Some of the past works have also put forward the fact that predefined (Park & Sandberg, 1991) and random (Huang et al., 2006) projections can be used together with a learned affine transformation to achieve competitive results on many of the classification tasks. However, the authors' proposal in the current paper is quite reversed.
Background
Convolutional neural networks (CNNs) are commonly used to solve a variety of spatial and temporal tasks. CNNs are usually composed of a stack of convolutional parameterized layers, spatial pooling layers and fully connected layers, separated by non-linear activation functions. Earlier architectures of CNNs (LeCun et al., 1998; Krizhevsky et al., 2012) used a set of fully-connected layers at later stage of the network, presumably to allow classification based on global features of an image.
Shortcomings of the final classification layer and its solution
Despite the enormous number of trainable parameters these layers added to the model, they are known to have a rather marginal impact on the final performance of the network (Zeiler & Fergus, 2014).
It has been shown previously that these layers could be easily compressed and reduced after a model was trained by simple means such as matrix decomposition and sparsification (Han et al., 2015). Modern architecture choices are characterized with the removal of most of the fully connected layers (Lin et al., 2013; Szegedy et al., 2015; He et al., 2016), that lead to better generalization and overall accuracy, together with a huge decrease in the number of trainable parameters. Additionally, numerous works showed that CNNs can be trained in a metric learning regime (Bromley et al., 1994; Schroff et al., 2015; Hoffer & Ailon, 2015), where no explicit classification layer was introduced and the objective regarded only distance measures between intermediate representations. Hardt & Ma (2017) suggested an all-convolutional network variant, where they kept the original initialization of the classification layer fixed with no negative impact on performance on the CIFAR-10 dataset.
Proposed Method
The aforementioned works provide evidence that fully-connected layers are in fact redundant and play a small role in learning and generalization. In this work, the authors have suggested that parameters used for the final classification transform are completely redundant, and can be replaced with a predetermined linear transform. This holds for even in large-scale models and classification tasks, such as recent architectures trained on the ImageNet benchmark (Deng et al., 2009).
Using a fixed classifier
Suppose the final representation obtained by the network (the last hidden layer) is represented as [math]\displaystyle{ x = F(z;\theta) }[/math] where [math]\displaystyle{ F }[/math] is assumed to be a deep neural network with input z and parameters θ, e.g., a convolutional network, trained by backpropagation.
In common NN models, this representation is followed by an additional affine transformation, [math]\displaystyle{ y = W^T x + b }[/math] ,where [math]\displaystyle{ W }[/math] and [math]\displaystyle{ b }[/math] are also trained by back-propagation.
For input [math]\displaystyle{ x }[/math] of [math]\displaystyle{ N }[/math] length, and [math]\displaystyle{ C }[/math] different possible outputs, [math]\displaystyle{ W }[/math] is required to be a matrix of [math]\displaystyle{ N × C }[/math]. Training is done using cross-entropy loss, by feeding the network outputs through a softmax activation
[math]\displaystyle{ v_i = \frac{e^{y_i}}{\sum_{j}^{C}{e^{y_j}}}, i ∈ }[/math] { [math]\displaystyle{ {1, . . . , C} }[/math] }
and reducing the expected negative log likelihood with respect to ground-truth target [math]\displaystyle{ t ∈ }[/math] { [math]\displaystyle{ {1, . . . , C} }[/math] }, by minimizing the loss function:
[math]\displaystyle{ L(x, t) = − log {v_t} = −{w_t}·{x} − b_t + log ({\sum_{j}^{C}e^{w_j . x + b_j}}) }[/math]
where [math]\displaystyle{ w_i }[/math] is the [math]\displaystyle{ i }[/math]-th column of [math]\displaystyle{ W }[/math].
Choosing the projection matrix
To evaluate the conjecture regarding the importance of the final classification transformation, the trainable parameter matrix [math]\displaystyle{ W }[/math] is replaced with a fixed orthonormal projection [math]\displaystyle{ Q ∈ R^{N×C} }[/math], such that [math]\displaystyle{ ∀ i ≠ j : q_i · q_j = 0 }[/math] and [math]\displaystyle{ || q_i ||_{2} = 1 }[/math], where [math]\displaystyle{ q_i }[/math] is the [math]\displaystyle{ i }[/math]th column of [math]\displaystyle{ Q }[/math]. This is ensured by a simple random sampling and singular-value decomposition
As the rows of classifier weight matrix are fixed with an equally valued [math]\displaystyle{ L_{2} }[/math] norm, we find it beneficial to also restrict the representation of [math]\displaystyle{ x }[/math] by normalizing it to reside on the [math]\displaystyle{ n }[/math]-dimensional sphere:
This allows faster training and convergence, as the network does not need to account for changes in the scale of its weights. However, it has now an issue that [math]\displaystyle{ q_i · \hat{x} }[/math] is bounded between −1 and 1. This causes convergence issues, as the softmax function is scale sensitive, and the network is affected by the inability to re-scale its input. This issue is amended with a fixed scale [math]\displaystyle{ T }[/math] applied to softmax inputs [math]\displaystyle{ f(y) = softmax(\frac{1}{T}y) }[/math], also known as the softmax temperature. However, this introduces an additional hyper-parameter which may differ between networks and datasets. So, the authors propose to introduce a single scalar parameter [math]\displaystyle{ \alpha }[/math] to learn the softmax scale, effectively functioning as an inverse of the softmax temperature [math]\displaystyle{ \frac{1}{T} }[/math]. The additional vector of bias parameters [math]\displaystyle{ b ∈ R^{C} }[/math] is kept the same and the model is trained using the traditional negative-log-likelihood criterion. Explicitly, the classifier output is now:
[math]\displaystyle{ v_i=\frac{e^{\alpha q_i · \hat{x} + b_i}}{\sum_{j}^{C} e^{\alpha q_j · \hat{x} + b_j}}, i ∈ }[/math] { [math]\displaystyle{ {1,...,C} }[/math]}
and the loss to be minimized is:
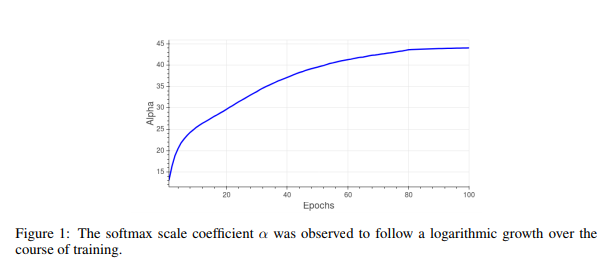
where [math]\displaystyle{ x }[/math] is the final representation obtained by the network for a specific sample, and [math]\displaystyle{ t ∈ }[/math] { [math]\displaystyle{ {1, . . . , C} }[/math] } is the ground-truth label for that sample. The behaviour of the parameter [math]\displaystyle{ \alpha }[/math] over time, which is logarithmic in nature, is shown in Figure 1.
Using a Hadmard matrix
To recall, Hadmard matrix (Hedayat et al., 1978) [math]\displaystyle{ H }[/math] is an [math]\displaystyle{ n × n }[/math] matrix, where all of its entries are either +1 or −1. Furthermore, [math]\displaystyle{ H }[/math] is orthogonal, such that [math]\displaystyle{ HH^{T} = nI_n }[/math] where [math]\displaystyle{ I_n }[/math] is the identity matrix. Instead of using the entire Hadmard matrix [math]\displaystyle{ H }[/math], a truncated version, [math]\displaystyle{ \hat{H} ∈ }[/math] {[math]\displaystyle{ {-1, 1} }[/math]}[math]\displaystyle{ ^{C \times N} }[/math] where all [math]\displaystyle{ C }[/math] rows are orthogonal as the final classification layer is such that:
This usage allows two main benefits:
- A deterministic, low-memory and easily generated matrix that can be used for classification.
- Removal of the need to perform a full matrix-matrix multiplication - as multiplying by a Hadamard matrix can be done by simple sign manipulation and addition.
Here, [math]\displaystyle{ n }[/math] must be a multiple of 4, but it can be easily truncated to fit normally defined networks. Also, as the classifier weights are fixed to need only 1-bit precision, it is now possible to focus our attention on the features preceding it.
Experimental Results
The authors have evaluated their proposed model on the following datasets:
CIFAR-10/100
About the dataset
CIFAR-10 is an image classification benchmark dataset containing 50,000 training images and 10,000 test images. The images are in color and contain 32×32 pixels. There are 10 possible classes of various animals and vehicles. CIFAR-100 holds the same number of images of same size, but contains 100 different classes.
Training Details
The authors trained a residual network ( He et al., 2016) on the CIFAR-10 dataset. The network depth was 56 and the same hyper-parameters as in the original work were used. A comparison of the two variants, i.e., the learned classifier and the proposed classifier with a fixed transformation is shown in Figure 2.
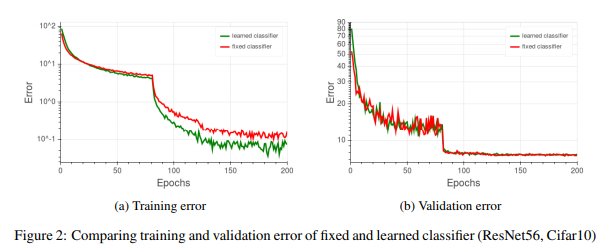
These results demonstrate that although the training error is considerably lower for the network with learned classifier, both models achieve the same classification accuracy on the validation set. The authors conjecture is that with the new fixed parameterization, the network can no longer increase the norm of a given sample’s representation - thus learning its label requires more effort. As this may happen for specific seen samples - it affects only training error.
The authors also compared using a fixed scale variable [math]\displaystyle{ \alpha }[/math] at different values vs. the learned parameter. Results for [math]\displaystyle{ \alpha = }[/math] {0.1, 1, 10} are depicted in Figure 3 for both training and validation error.