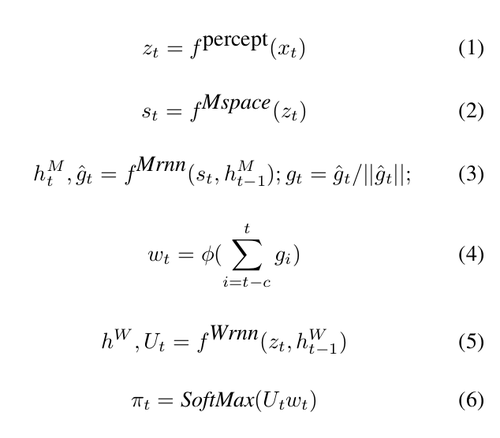FeUdal Networks for Hierarchical Reinforcement Learning: Difference between revisions
No edit summary |
(→Model) |
||
| Line 21: | Line 21: | ||
A high-level explanation of the model is as follows: | A high-level explanation of the model is as follows: | ||
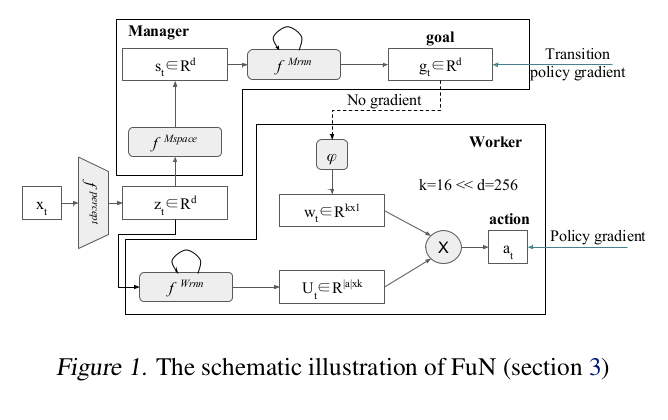
The Manager computes a latent state representation <math>s_t</math> and outputs a goal vector <math>g_t</math> . The Worker outputs actions based on the environment observation, its own state, and the Manager’s goal. A perceptual module computes intermediate representation, <math>z_t</math> of the environment observation <math>x_t</math>. The Manager’s goals <math>g_t</math> are trained using an approximate transition policy gradient. The Worker is then trained via intrinsic reward which stimulates it to output actions that will achieve the goals set by the Manager. | The Manager computes a latent state representation <math>s_t</math> and outputs a goal vector <math>g_t</math> . The Worker outputs actions based on the environment observation, its own state, and the Manager’s goal. A perceptual module computes intermediate representation, <math>z_t</math> of the environment observation <math>x_t</math>, and is shared as input by both Manager and Worker. The Manager’s goals <math>g_t</math> are trained using an approximate transition policy gradient. The Worker is then trained via intrinsic reward which stimulates it to output actions that will achieve the goals set by the Manager. | ||
<center> | <center> | ||
Revision as of 23:36, 5 November 2017
Introduction
Even though deep reinforcement learning has been hugely successful in a variety of domains, it has not been able to succeed in environments which have sparsely spaced reward signals and encounters the major challenge of long-term credit assignment, where the agent is not able to attribute a reward to an action taken several timesteps back.
This paper proposes a hierarchical reinforcement learning architecture (HRL), called FeUdal Networks (FuN), which has been inspired from Feudal Reinforcement Learning (FRL)[3]. It is a fully-differentiable neural network with two levels of hierarchy – a Manager module at the top level and a Worker module below. The Manager sets abstract goals, which are learned, at a lower temporal resolution in a latent state-space. The Worker operates at a higher temporal resolution and produces primitive actions at every tick of the environment, motivated to follow the goals received from Manager, by an intrinsic reward.
The key contributions of the authors in this paper are: (1) A consistent, end-to-end differentiable FRL inspired HRL. (2) A novel, approximate transition policy gradient update for training the Manager (3) The use of goals that are directional rather than absolute in nature. (4) Dilated LSTM – a novel RNN design for the Manager that allows gradients to flow through large hops in time.
The experiments conducted on several tasks which involve sparse rewards show that FuN significantly outperforms a strong baseline agent on tasks that involve long-term credit assignment and memorization.
Related Work
Several hierarchical reinforcement learning models were proposed to solve this problem. The options framework [4] considers the problem with a two-level hierarchy, with options being typically learned using sub-goals and ‘pseudo-rewards’ that are provided explicitly. Whereas, the option-critic architecture[1] uses the policy gradient theorem for learning options in an end-to-end fashion. A problem with learning options end-to-end is that they tend to a trivial solution where: (i) only one option is active, which solves the whole task; (ii) a policy-over-options changes options at every step, micro-managing the behavior. The authors state that the option-critic architecture is the only other end-to-end trainable system with sub-policies.
Non-hierarchical deep RL (non-HRL) methods using auxiliary losses and rewards such as pseudo count for exploration[2] have significantly improved results by stimulating agents to explore new parts of the state space. The UNREAL agent[9] is another non-HRL method that showed a strong improvement using unsupervised auxiliary tasks.
Model
A high-level explanation of the model is as follows:
The Manager computes a latent state representation [math]\displaystyle{ s_t }[/math] and outputs a goal vector [math]\displaystyle{ g_t }[/math] . The Worker outputs actions based on the environment observation, its own state, and the Manager’s goal. A perceptual module computes intermediate representation, [math]\displaystyle{ z_t }[/math] of the environment observation [math]\displaystyle{ x_t }[/math], and is shared as input by both Manager and Worker. The Manager’s goals [math]\displaystyle{ g_t }[/math] are trained using an approximate transition policy gradient. The Worker is then trained via intrinsic reward which stimulates it to output actions that will achieve the goals set by the Manager.
Manager and Worker are recurrent networks ([math]\displaystyle{ {h^M} }[/math] and [math]\displaystyle{ {h^W} }[/math] being their internal states). [math]\displaystyle{ \phi }[/math] is a linear transform that maps a goal [math]\displaystyle{ g_t }[/math] into an embedding vector [math]\displaystyle{ w_t \in {R^k} }[/math] , which is then combined with matrix [math]\displaystyle{ U_t }[/math] (Worker's output) via a matrix-vector product to produce policy [math]\displaystyle{ \pi }[/math] – vector of probabilities over primitive actions. The projection [math]\displaystyle{ \phi }[/math] is linear, with no biases, and is learnt with gradients coming from the Worker’s actions.Since [math]\displaystyle{ \phi }[/math] has no biases it can never produce a constant non-zero vector – which is the only way the setup could ignore the Manager’s input. This makes sure that the goal output by the Manager always influences the final policy.
Learning
The learning considers a standard reinforcement learning setup where the goal of the agent is to maximize the discounted return [math]\displaystyle{ R_t = \sum_{k=0}^{∞} \gamma^k r_{t+k+1} }[/math]; where [math]\displaystyle{ \gamma \in [0,1]; r_t }[/math] is the reward from environment for action at timestep, [math]\displaystyle{ t }[/math]. The agent's behavior is defined by its action-selection policy, [math]\displaystyle{ \pi }[/math].
Since FuN is fully differentiable, the authors could have trained it end-to-end using a policy gradient algorithm operating on the actions taken by the Worker such the outputs [math]\displaystyle{ g }[/math] of the Manager would be trained by gradients coming from the Worker. This, however, would deprive Manager’s goals [math]\displaystyle{ g }[/math] of any semantic meaning, making them just internal latent variables of the model. So instead, Manager is independently trained to predict advantageous directions (transitions) in state space and to intrinsically reward the Worker to follow these directions.
Update rule for manager:
[math]\displaystyle{ \nabla g_t = A_t^M \nabla_\theta d_{cos}(s_{t+c} - s_t, g_t(\theta)) }[/math]
In above equation, [math]\displaystyle{ d_{cos}(\alpha, \beta) = \alpha^T \beta/(|\alpha||\beta|) }[/math] is the cosine similarity between two vectors and [math]\displaystyle{ A_t^M = R_t - V_t^M(x_t,\theta) }[/math] is the Manager’s advantage function, computed using a value function estimate [math]\displaystyle{ V_t^M(x_t,\theta) }[/math] from the internal critic.
The intrinsic reward that encourages the Worker to follow the goals are defined as:
[math]\displaystyle{ r_t^I = 1/c \sum_{i=1}^c d_{cos}(s_t - s_{t-i}, g_{t-i}) }[/math]
Compared to FRL[3], which advocated concealing the reward from lower levels of the hierarchy, the Worker in FuN network is trained using an advantage actor-critic[5] to maximise a weighted sum [math]\displaystyle{ R_t + α R_t^I }[/math] , where [math]\displaystyle{ α }[/math] is a hyper-parameter that regulates the influence of the intrinsic reward:
[math]\displaystyle{ \nabla {\pi}_t = A_t^D \nabla_\theta log \pi (a_t|x_t;\theta) }[/math]
The Advantage function [math]\displaystyle{ A_t^D = (R_t + \alpha R_t^I - V_t^D(x_t;\theta)) }[/math] is calculated using an internal critic, which estimates the value functions for both rewards.
Transition Policy Gradient
The update rule for the Manager given above is a novel form of policy gradient with respect to a model of the Worker’s behavior. The Worker can follow a complex trajectory but it is not necessarily required to learn from these samples. If the trajectories can be predicted, by modeling the transitions, then the policy gradient of the predicted transition can be followed instead of the Worker's actual path. FuN assumes a particular form for the transition model: that the direction in state-space, [math]\displaystyle{ s_{t+c} − s_t }[/math], follows a von Mises-Fisher distribution.
Architecture
The perceptual module [math]\displaystyle{ f^{percept} }[/math] is a convolutional network (CNN) followed by a fully connected layer. Each convolutional and fully-connected layer is followed by a rectifier non-linearity. [math]\displaystyle{ f_{Mspace} }[/math], which is another fully connected layer followed by a rectifier non-linearity, is used to compute the state space, which the Manager uses to formulate goals. The Worker’s recurrent network [math]\displaystyle{ f^{Wrnn} }[/math] is a standard LSTM[6].
The Manager uses a novel architecture called a dilated LSTM (dLSTM), which operates at lower temporal resolution than the data stream. It is similar to dilated convolutional networks[7] and clockwork RNN. For a dilation radius r, the network is composed of r separate groups of sub-states or ‘cores’, denoted by [math]\displaystyle{ h = \{\hat{h}^i\}_{i=1}^r }[/math]. At time [math]\displaystyle{ t }[/math], the network is governed by the following equations: [math]\displaystyle{ \hat{h}_t^{t\%r},g_t = LSTM(s_t, \hat{h}_{t-1}^{t\%r};\theta^{LSTM}) }[/math] where % denotes the modulo operation and allows us to indicate which group of cores is currently being updated. At each time step, only the corresponding part of the state is updated and the output is pooled across the previous c outputs. This allows the r groups of cores inside the dLSTM to preserve the memories for long periods, yet the dLSTM as a whole is still able to process and learn from every input experience and is also able to update its output at every step.
Experiments
The baseline the authors are using is a recurrent LSTM[6] network on top of a representation learned by a CNN. The A3C method[5] is used for all reinforcement learning experiments. Backpropagation through time (BPTT)[8] is run after K forward passes of a network or if a terminal signal is received. For each method, 100 experiments were run. A training epoch is defined as one million observations.
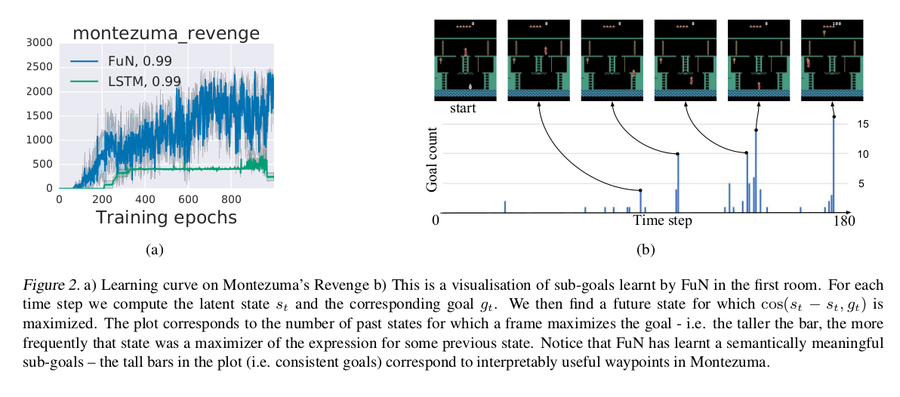
Montezuma’s Revenge
Montezuma’s revenge is a prime example of an environment with sparse rewards. FuN starts learning much earlier and achieves much higher scores. It takes > 300 epochs for LSTM to reach the score 400, which corresponds to solving the first room (take the key, open a door). FuN solves the first room in less than 200 epochs and immediately moves on to explore further, eventually visiting several other rooms and scoring up to 2600 points.
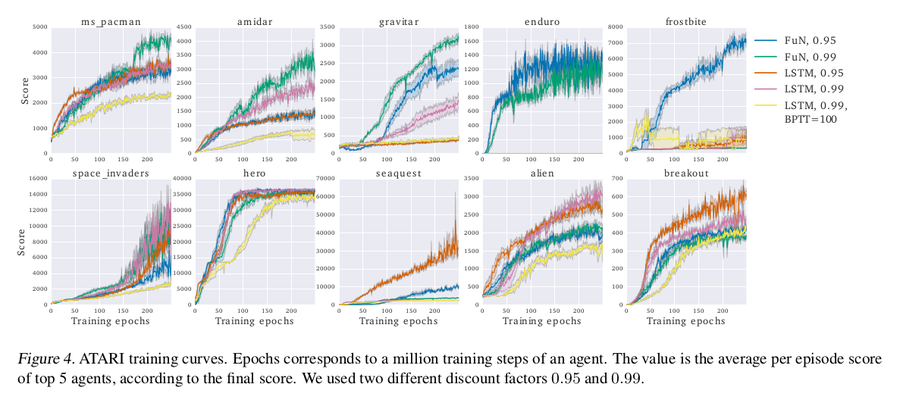
ATARI
The experiment was run on a diverse set of ATARI games, some of which involve long-term credit assignment and some which are more reactive. Enduro stands out as all the LSTM agents completely fail at it. Frostbite is a hard game that requires both long-term credit assignment and good exploration. The best-performing frostbite agent is FuN with 0.95 Manager discount, which outperforms the rest by a factor of 7. The other results can be seen in the figure.
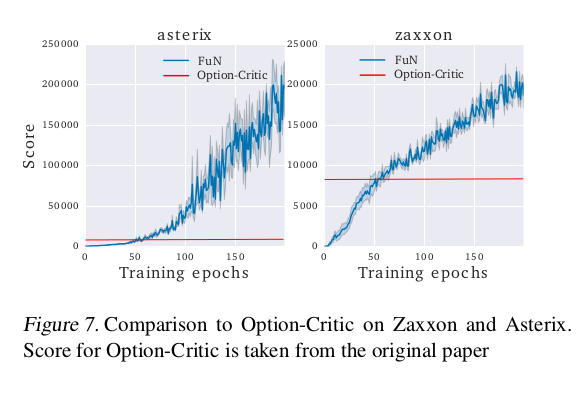
Comparing the option-critic architecture
FuN network was run on the same games as Option-Critic (Asterix, Ms. Pacman, Seaquest, and Zaxxon) and after 200 epochs it achieves a similar score on Seaquest, doubles it on Ms. Pacman, more than triples it on Zaxxon and gets more than 20x improvement on Asterix.
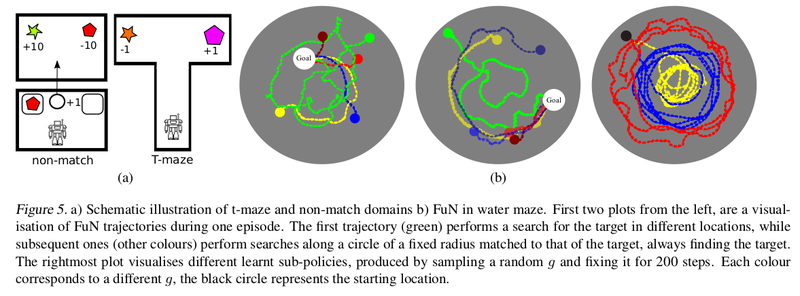
Memory in Labyrinth
DeepMind Lab (Beattie et al., 2016) is a first-person 3D game platform extended from OpenArena. The games on which the experiments were run on include a Water maze, T-maze, and Non-match (which is a visual memorization task). FuN consistently outperforms the LSTM baseline – it learns faster and also reaches a higher final reward. Interestingly, the LSTM agent doesn’t appear to use its memory for water maze task at all, always circling the maze at the roughly the same radius.
Ablative Analysis
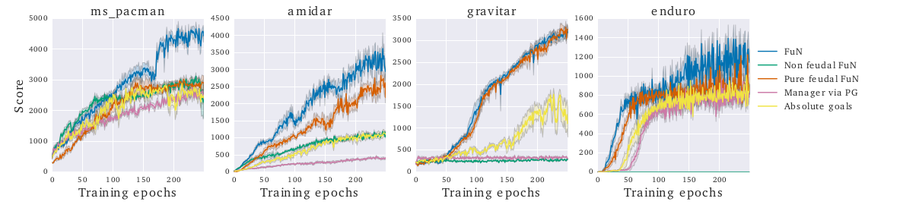
Empirical evaluation of the main contributions of this paper:
Transition policy gradient
Experiments were run on modified FuN networks in which: 1) the Managers output g is trained with gradients coming directly from the Worker and no intrinsic reward is used, 2) g is learned using a standard policy gradient approach with the Manager emitting the mean of a Gaussian distribution from which goals are sampled, 3) a variant of FuN in which g specifies absolute, rather than relative/directional, goals and 4) a purely feudal version of FuN – in which the Worker is trained from the intrinsic reward alone. The experiments (Figure 8) reveal that, although alternatives do work to some degree their performance is significantly inferior.
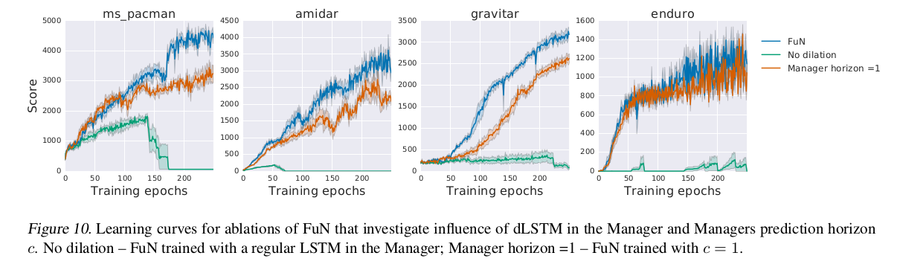
Temporal resolution ablations
To test the effectiveness of the dilation LSTM, FuN was compared with two baselines 1) the Manager uses a vanilla LSTM with no dilation; 2) FuN with Manager’s prediction horizon c = 1. The non-dilated LSTM fails catastrophically, most likely overwhelmed by the recurrent gradient. Reducing the horizon c to 1 did hurt the performance, although not that much, which means that even at high temporal resolution Manager captures certain properties of the underlying MDP.
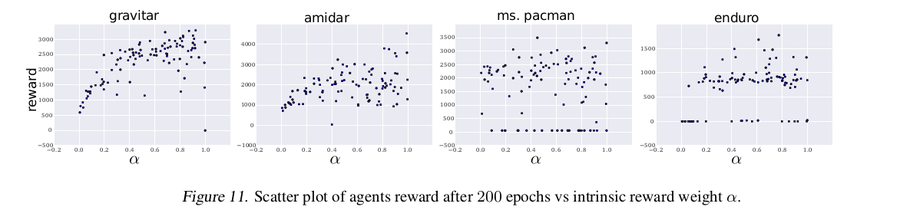
Intrinsic motivation weight
Evaluates the effect of weight [math]\displaystyle{ α }[/math] which regulates the relative weight of intrinsic reward. Figure below shows scatter plots of agents final score vs α hyper-parameter where there is a clear improvement in score for high [math]\displaystyle{ \alpha }[/math] in some games.
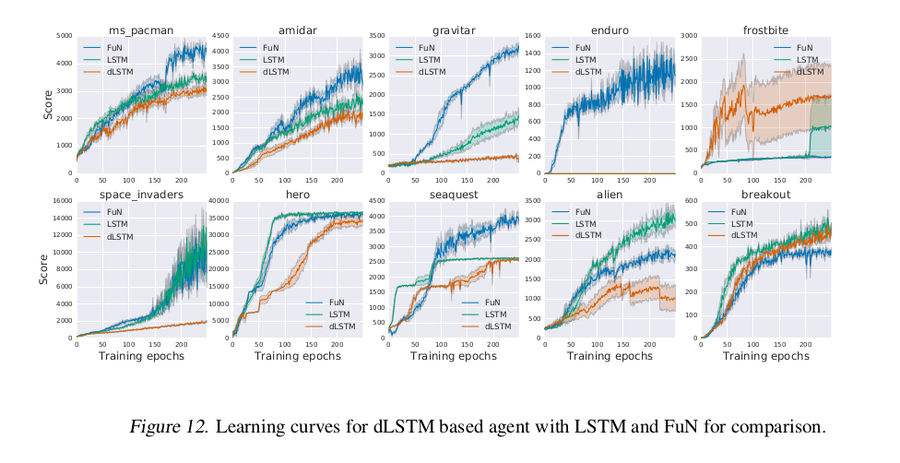
Dilate LSTM agent baseline
For this experiment, just the dLSTM is used in an agent on top of a CNN, without the rest of FuN structures. Figure below plots the learning curves for FuN, LSTM, and dLSTM agents. dLSTM generally underperforms both LSTM and FuN.
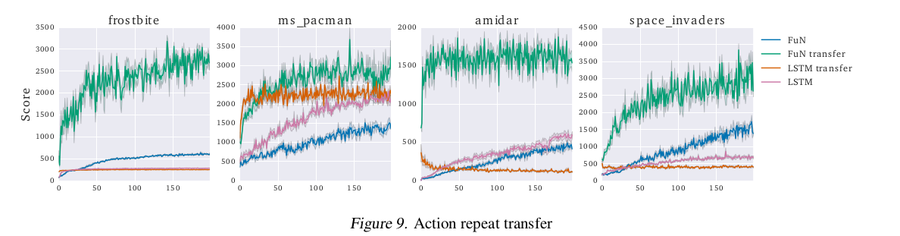
ATARI action repeat transfer
This experiment is to demonstrate that the transition policy can be transferred between agents with different embodiment, for example, across agents with different action repeat on ATARI. The figure below shows the corresponding learning curves. The transferred FuN agent (green curve) significantly outperforms every other method.
Conclusion
FuN currently holds state-of-the-art score in the Atari game, Montezuma's revenge among HRL methods. It is a novel approach to hierarchical reinforcement learning which separates the goal setting behavior from the generation of action primitives. This creates a natural hierarchy that is stable and the experiments clearly demonstrate that the FeUdal network makes long-term credit assignment and memorization more tractable.
Deeper hierarchies by setting goals at multiple time scales is an avenue for further research. The modular structure looks promising for transfer and multitask learning as well.
References
- Bacon, Pierre-Luc, Precup, Doina, and Harb, Jean. The option-critic architecture. In AAAI, 2017.
- Bellemare, Marc, Srinivasan, Sriram, Ostrovski, Georg, Schaul, Tom, Saxton, David, and Munos, Remi. Unifying count-based exploration and intrinsic motivation.In NIPS, 2016a.
- Dayan, Peter and Hinton, Geoffrey E. Feudal reinforcement learning. In NIPS. Morgan Kaufmann Publishers,1993.
- Sutton, Richard S, Precup, Doina, and Singh, Satinder. Between mdps and semi-mdps: A framework for temporal abstraction in reinforcement learning. Artificial intelligence, 1999.
- Mnih, Volodymyr, Badia, Adria Puigdomenech, Mirza,Mehdi, Graves, Alex, Lillicrap, Timothy P, Harley, Tim,Silver, David, and Kavukcuoglu, Koray. Asynchronousmethods for deep reinforcement learning. ICML, 2016.
- Hochreiter, Sepp and Schmidhuber, Jürgen. Long short-term memory. Neural computation, 1997.
- Yu, Fisher and Koltun, Vladlen. Multi-scale context aggregation by dilated convolutions. ICLR, 2016.
- Mozer, Michael C. A focused back-propagation algorithm for temporal pattern recognition. Complex systems, 1989.
- Jaderberg, Max, Mnih, Volodymyr, Czarnecki, Wojciech Marian, Schaul, Tom, Leibo, Joel Z, Silver,David, and Kavukcuoglu, Koray. Reinforcement learning with unsupervised auxiliary tasks. arXiv preprint arXiv:1611.05397, 2016.
- A. S. Vezhnevets, S. Osindero, T. Schaul, N. Heess, M. Jaderberg, D. Silver, and K. Kavukcuoglu. Feudal networks for hierarchical reinforcement learning. arXiv preprint arXiv:1703.01161, 2017.