Extreme Multi-label Text Classification
Presented By
Mohan Wu
Introduction
In this paper, the authors are interested a field of problems called extreme classification. These problems involve training a classifier to give the most relevant tags for any given text; the difficulties arise from the fact that the label set is so large so that most models would fail. The authors propose a new model called APLC-XLNet which fine-tunes the generalized autoregressive pre-trained model (XLNet) by using Adaptive Probabilistic Label Clusters (APLC) to calculate cross-entropy loss. This method takes advantage of unbalanced label distributions by forming clusters to reduce training time. The authors experimented on five different datasets and showed that their method far outweighs the existing state-of-the-art models.
Motivation
Extreme multi-label text classification (XMTC) has applications in many recent problems such as providing word representations of a large vocabulary [1], tagging Wikipedia with relevant labels [2], and giving product descriptions for search advertisements [3]. The authors are motivated by the shortcomings of traditional methods in the creation of XMTC. For example, one such method of classifying text is the bag-of-words (BOW) approach where a vector represents the frequency of a word in a corpus. However, BOW does not consider the location of the words so it cannot determine context and semantics. Motivated by the success of transfer learning in a wide range of natural language processing (NLP) problems, the authors propose to adapt XLNet [4] to the XMTC problem. The final challenge is the nature of the labeling distribution can be very sparse for some labels. The authors solve this problem by combining the Probabilistic Label Tree [5] method and the Adaptive Softmax [6] to propose APLC.
Related Work
Two approaches have been proposed to solve the XMTC problem: traditional BOW techniques, and modern deep learning models.
BOW Approaches
The traditional BOW approach contains three different approaches: one-vs-all approaches, embedding-based approaches, and tree-based approaches.
Intuitively, researchers can apply the one-vs-all approach in which they can fit a classifier for each label and thus XMTC reduces to a binary classification problem. This technique has been shown to achieve high accuracy; however, due to a large number of labels, this approach is very computationally expensive. There have been some techniques to reduce the complexity by pruning weights (PDSparse) to induce sparsity but still, this method is quite expensive. PPDSparse was introduced to parallelize PDSparse in a large-scaled distributed setting. Additionally, DiSMEC was introduced as another extension to PDSparse that allows for a distributed and parallel training mechanism which can be done efficiently by a novel negative sampling technique in addition to the pruning of spurious weights. Another approach is to simply apply a dimensional reduction technique on the label space. However, doing so has shown to have serious negative effects on the prediction accuracy due to loss of information in the compression phase. Finally, another approach is to use a tree to partition labels into groups based on similarity. This approach has shown to be quite fast but unfortunately, due to the problems with BOW methods, the accuracy is poor.
In embedding-based approaches, the high-dimensional label space is projected into a low-dimensional one by exploiting label correlations and sparsity. Embedding methods may pay a heavy price in terms of prediction accuracy due to the loss of information in the compression phase.
In tree-based methods, a hierarchical tree structure is learned to partition the instances or labels into different groups so that similar ones can be in the same group. The whole set, initially assigned to the root node, is partitioned into a fixed number of k subsets corresponding to k child nodes of the root node. The partition process is repeated until a stopping condition is satisfied on the subsets.
Deep Learning Approaches
Unlike BOW approaches, deep learning can learn dense representations of the corpus using context and semantics. One such example is X-BERT[7] which divides XTMC problems into 3 steps. First, it partitions the label set into clusters based on similarity. Next, it fits a BERT model on the label clusters for the given corpus. Finally, it trains simple linear classifiers to rank the labels in each cluster. Since there are elements of traditional techniques in X-BERT, namely, the clustering step and the linear classifier step, the authors propose to improve upon this approach.
APLC-XLNet
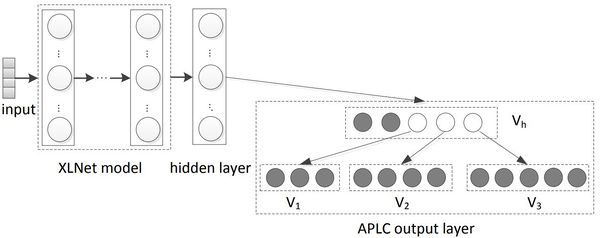
APLC-XLNet consists of three parts: the pre-trained XLNet-Base as the base, the APLC output layer, and a fully connected hidden layer connecting the pooling layer of XLNet as the output layer, as it can be seen in figure 1. To recap, XLNet [8] is a generalized autoregressive pretraining language model based upon capturing bidirectional contexts through maximizing the expected likelihood over all permutations of the factorization
the order which can be expressed as follows:
\begin{equation} \underset{\theta}{\max}{ E_{z \sim Z_T}[\sum_{t=1}^{T} \log {p_{\theta}(x_{z_{t}}|x_{z<t})}] } \end{equation}
where [math]\displaystyle{ \theta }[/math] denotes the parameters of the model, [math]\displaystyle{ Z_T }[/math] is the set of all possible permutations of the sequence with length T, [math]\displaystyle{ z_t }[/math] is the [math]\displaystyle{ t }[/math]-th element and [math]\displaystyle{ z \lt t }[/math] deontes the preceding [math]\displaystyle{ t-1 }[/math] elements in a permutation [math]\displaystyle{ z }[/math].
One major challenge in XTMC problems is that most data fall into a small group of labels. To tackle this challenge, the authors propose partitioning the label set into one head cluster, [math]\displaystyle{ V_h }[/math], and many tail clusters, [math]\displaystyle{ V_1 \cup \ldots \cup V_K }[/math]. The head cluster contains the most popular labels while the tail clusters contain the rest of the labels. The clusters are then inserted in a 2-level tree where the root node is the head cluster and the leaves are the tail clusters. Using this architecture improves computation times significantly since most of the time the data stops at the root node.
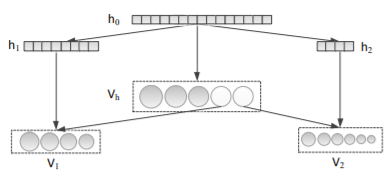
The authors define the probability of each label as follows:
\begin{equation} p(y_{ij} | x) = \begin{cases} p(y_{ij}|x) & \text{if } y_{ij} \in V_h \\ p(V_t|x)p(y_{ij}|V_t,x) & \text{if } y_{ij} \in V_t \end{cases} \end{equation}
where [math]\displaystyle{ x }[/math] is the feature of a given sample, [math]\displaystyle{ y_{ij} }[/math] is the j-th label in the i-th sample, and [math]\displaystyle{ V_t }[/math] is the t-th tail cluster. Let [math]\displaystyle{ Y_i }[/math] be the set of labels for the i-th sample, and define [math]\displaystyle{ L_i = |Y_i| }[/math]. The authors propose an intuitive objective loss function for multi-label classification:
\begin{equation} J(\theta) = -\frac{1}{\sum_{i=1}^N L_i} \sum_{i=1}^N \sum_{j \in Y_i} (y_{ij} logp(y_{ij}) + (1 - y_{ij}) log(1- p(y_{ij})) \end{equation} where [math]\displaystyle{ N }[/math] is the number of samples, [math]\displaystyle{ p(y_{ij}) }[/math] is defined above and [math]\displaystyle{ y_{ij} \in \{0, 1\} }[/math].
The number of parameters in this model is given by: \begin{equation} N_{par} = d(l_h + K) + \sum_{i=1}^K \frac{d}{q^i}(d+l_i) \end{equation} where [math]\displaystyle{ d }[/math] is the dimension of the hidden state of [math]\displaystyle{ V_h }[/math], [math]\displaystyle{ q }[/math] is a decay variable, [math]\displaystyle{ l_h = |V_h| }[/math] and [math]\displaystyle{ l_i = |V_i| }[/math]. Furthermore, the computational cost can be expressed as follows: \begin{align} C &= C_h + \sum_{i=1}^K C_i \\ &= O(N_b d(l_h + K)) + O(\sum_{i=1}^K p_i N_b \frac{d}{q^i}(l_i + d)) \end{align} where [math]\displaystyle{ N_b }[/math] is the batch size.
Note that in practical settings where [math]\displaystyle{ K\ll l_h }[/math] and [math]\displaystyle{ d\ll l_i }[/math] the computational cost can be rewritten as [math]\displaystyle{ O(N_b d(l_h + \sum_{i=1}^Kp_i\frac{l_i}{q_i})) }[/math]. Furthermore, the authors pointed out that, assuming all of [math]\displaystyle{ l_i }[/math] are fixed, the computational complexity can be reduced by configuring the model so that [math]\displaystyle{ p_i }[/math] is small, which corresponds to a low probability of a batch entering the tail cluster [math]\displaystyle{ i }[/math], as the computational burden is dominated by the cost of entering tail clusters.
Training APLC-XLNet
Training APLC-XLNet essentially boils down to training its three parts. The authors suggest using discriminative fine-tuning method[9] to train the model entirely while assigning different learning rates to each part. Since XLNet is pretrained, the learning rate, [math]\displaystyle{ \eta_x }[/math], should be small, while the output layer is specific to this type of problem so its learning rate, [math]\displaystyle{ \eta_a }[/math], should be large. For the connecting hidden layer, the authors chose a learning rate, [math]\displaystyle{ \eta_h }[/math], such that [math]\displaystyle{ \eta_x \lt \eta_h \lt \eta_a }[/math]. For each of the learning rates, the authors suggest a slanted triangular learning schedule[9] defined as: \begin{equation} \eta = \begin{cases} \eta_0 \frac{t}{t_w} & \text{if } t \leq t_w \\ \eta_0 \frac{t_a - t}{t_a - t_w} & \text{if } t > t_w \end{cases} \end{equation} where [math]\displaystyle{ \eta_0 }[/math] is the starting learning rate, [math]\displaystyle{ t }[/math] is the current step, [math]\displaystyle{ t_w }[/math] is the chosen warm-up threshold and [math]\displaystyle{ t_a }[/math] is the total number of steps. The objective here is to motivate the model to converge quickly to the suitable space at the beginning and then refine the parameters. Learning rates are first increased linearly, and then decayed gradually according to the strategy.
Results
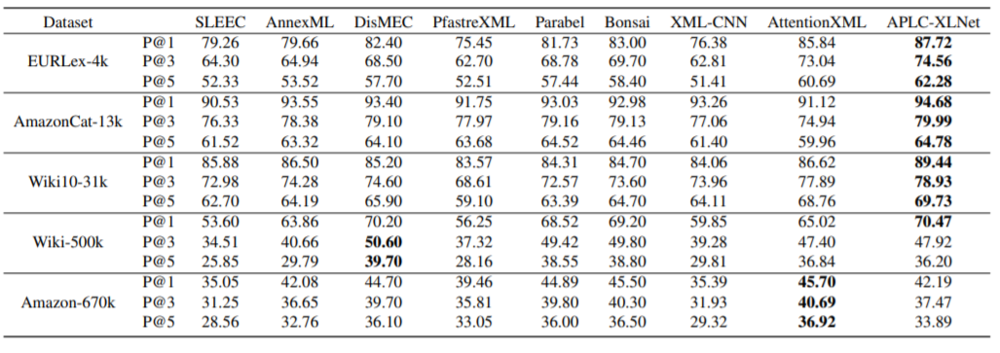
The authors tested the APLC-XLNet model in several benchmark datasets against current state-of-the-art baselines, including two embedding based models, SLEEC and AnnexML, the 1-vs-all model DisMEC, three tree-based approaches, PfastreXML, Parabel and Bonsai, and two deep learning approaches, XML-CNN and AttentionXML. The evaluation metric, P@k is defined as: \begin{equation} P@k = \frac{1}{k} \sum_{i \in rank_k(\hat{y})} y_i \end{equation} where [math]\displaystyle{ rank_k(\hat{y}) }[/math] is the top k ranked probability in the prediction vector, [math]\displaystyle{ \hat{y} }[/math].
As shown in the table below, APLC-XLNet outperforms the two embedding based models, SLEEC and AnnexML, across all five datasets. It outperforms DisMEC on three datasets except for Wiki-500k and Amazon-670k. Among the three tree based methods, Bonsai performs the best. And APLC-XLNet outperforms Bonsai on three datasets. At last, APLC-XLNet also outperforms the deep learning methods on four datasets.
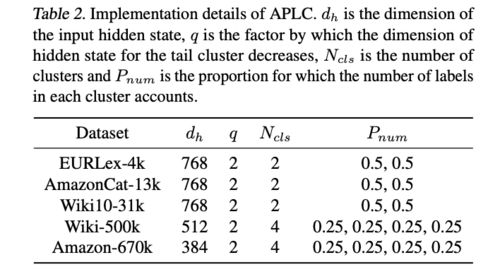
A SentencePiece tokenizer is used to preprocess raw text. The sentence is split up into small tokens as words. The following table (2) represents APLC's implementation details.
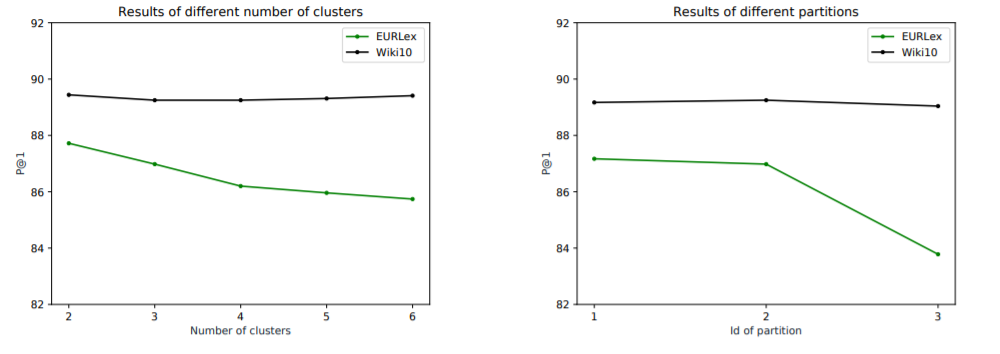
To help with tuning the model in the number of clusters and different partitions, the authors experimented on two different datasets: EURLex and Wiki10.
The three different partitions in the second graph the authors used were (0.7, 0.2, 0.1), (0.33, 0.33, 0.34), and (0.1, 0.2, 0.7) where 3 clusters were fixed.
Source Code
The Source Code for the paper can be found here: https://github.com/huiyegit/APLC_XLNet
Conclusion
The authors have proposed a new deep learning approach to solve the XMTC problem based on XLNet, namely, APLC-XLNet. APLC-XLNet consists of three parts: the pretrained XLNet that takes the input of the text, a connecting hidden layer, and finally an APLC output layer to give the rankings of relevant labels. Their experiments show that APLC-XLNet has better results in several benchmark datasets over the current state-of-the-art models.
Critques
The authors chose to use the same architecture for every dataset. The model does not achieve state-of-the-art performance on the larger datasets. Perhaps, a more complex model in the second part of the model could help achieve better results. The authors also put a lot of effort in explaining the model complexity for APLC-XLNet but does not compare it other state-of-the-art models. A table of model parameters and complexity for each model could be helpful in explaining why their techniques are efficient.
In their implementation, the label set was partitioned into clusters in a heuristic manner by experimenting different number of clusters and partition proportion. There might be a better model-based method to choose the partition structure.
References
[1] Mikolov, T., Kombrink, S., Burget, L., Cernock ˇ y, J., and ` Khudanpur, S. Extensions of recurrent neural network language model. In 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 5528–5531. IEEE, 2011.
[2] Dekel, O. and Shamir, O. Multiclass-multilabel classification with more classes than examples. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, pp. 137–144, 2010.
[3] Jain, H., Prabhu, Y., and Varma, M. Extreme multi-label loss functions for recommendation, tagging, ranking & other missing label applications. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 935–944. ACM, 2016.
[4] Yang, W., Xie, Y., Lin, A., Li, X., Tan, L., Xiong, K., Li, M., and Lin, J. End-to-end open-domain question answering with BERTserini. In NAACL-HLT (Demonstrations), 2019a.
[5] Jasinska, K., Dembczynski, K., Busa-Fekete, R., Pfannschmidt, K., Klerx, T., and Hullermeier, E. Extreme f-measure maximization using sparse probability estimates. In International Conference on Machine Learning, pp. 1435–1444, 2016.
[6] Grave, E., Joulin, A., Cisse, M., J ´ egou, H., et al. Effi- ´ cient softmax approximation for gpus. In Proceedings of the 34th International Conference on Machine LearningVolume 70, pp. 1302–1310. JMLR.org, 2017
[7] Wei-Cheng, C., Hsiang-Fu, Y., Kai, Z., Yiming, Y., and Inderjit, D. X-BERT: eXtreme Multi-label Text Classification using Bidirectional Encoder Representations from Transformers. In NeurIPS Science Meets Engineering of Deep Learning Workshop, 2019.
[8] Yang, Zhilin, et al. "Xlnet: Generalized autoregressive pretraining for language understanding." Advances in neural information processing systems. 2019.
[9] Howard, J. and Ruder, S. Universal language model finetuning for text classification. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pp. 328–339, 2018