Efficient kNN Classification with Different Numbers of Nearest Neighbors: Difference between revisions
| Line 63: | Line 63: | ||
The optimal ''k'' value for training sample 1 would be 2 since the correlation between training sample 1 and both training samples 2 and 4 is non-zero. | The optimal ''k'' value for training sample 1 would be 2 since the correlation between training sample 1 and both training samples 2 and 4 is non-zero. | ||
==== Train a Decision Tree using ''k'' as the label ==== | |||
=== k*Tree Classification === | === k*Tree Classification === | ||
Revision as of 14:42, 28 November 2020
Presented by
Cooper Brooke, Daniel Fagan, Maya Perelman
Introduction
Unlike popular parametric approaches which first utilizes training observations to learn a model and subsequently predict test samples with this model, the non-parametric k-nearest neighbors (kNNs) method classifies observations with a majority rules approach. kNN classifies test samples by assigning them the label of their k closest training observation (neighbours). This method has become very popular due to its significant performance and easy implementation.
There are two main approaches to conduct kNN classification. The first is to use a fixed k value to classify all test samples. The second is to use a different k value for each test sample. The former, while easy to implement, has proven to be impractical in machine learning applications. Therefore, interest lies in developing an efficient way to apply a different optimal k value for each test sample. The authors of this paper present the kTree and k*Tree methods to solve this research question.
Previous Work
Previous work on finding an optimal fixed k value for all test samples is well-studied. Zhang et al. [1] incorporated a certainty factor measure to solve for an optimal fixed k. This resulted in the conclusion that k should be [math]\displaystyle{ \sqrt{n} }[/math] (where n is the number of training samples) when n > 100. The method Song et al.[2] explored involved selecting a subset of the most informative samples from neighbourhoods. Vincent and Bengio [3] took the unique approach of designing a k-local hyperplane distance to solve for k. Premachandran and Kakarala [4] had the solution of selecting a robust k using the consensus of multiple rounds of kNNs. These fixed k methods are valuable however are impractical for data mining and machine learning applications.
Finding an efficient approach to assigning varied k values has also been previously studied. Tuning approaches such as the ones taken by Zhu et al. as well as Sahugara et al. have been popular. Zhu et al. [5] determined that optimal k values should be chosen using cross validation while Sahugara et al. [6] proposed using Monte Carlo validation to select varied k parameters. Other learning approaches such as those taken by Zheng et al. and Góra and Wojna also show promise. Zheng et al. [7] applied a reconstruction framework to learn suitable k values. Góra and Wojna [8] proposed using rule induction and instance-based learning to learn optimal k-values for each test sample. While all these methods are valid, their processes of either learning varied k values or scanning all training samples are time-consuming.
Motivation
Due to the previously mentioned drawbacks of fixed-k and current varied-k kNN classification, the paper’s authors sought to design a new approach to solve for different k values. The kTree and k*Tree approach seeks to calculate optimal values of k while avoiding computationally costly steps such as cross validation.
A secondary motivation of this research was to ensure that the kTree method would perform better than kNN using fixed values of k given that running costs would be similar in this instance.
Approach
kTree Classification
The proposed kTree method is illustrated by the following flow chart:
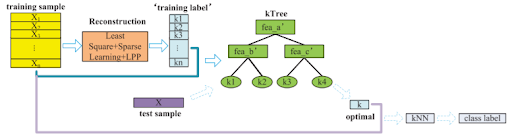
Reconstruction
The first step is to use the training samples to reconstruct themselves. The goal of this is to find the matrix of correlations between the training samples themselves, [math]\displaystyle{ \textbf{W} }[/math], such that the distance between an individual training sample and the corresponding correlation vector multiplied by the entire training set is minimized. This least square loss function where [math]\displaystyle{ \mathbf{X} }[/math] represents the training set can be written as:
$$\begin{aligned} \mathop{min}_{\textbf{W}} \sum_{i=1}^n ||Xw_i - x_i||^2 \end{aligned}$$
In addition, an [math]\displaystyle{ l_1 }[/math] regularization term multiplied by a tuning parameter, [math]\displaystyle{ \rho_1 }[/math], is added to ensure that sparse results are generated as the objective is to minimize the number of training samples that will eventually be depended on by the test samples.
The least square loss function is then further modified to account for samples that have similar values for certain features yielding similar results. After some transformations, this second regularization term that has tuning parameter [math]\displaystyle{ \rho_2 }[/math] is:
$$\begin{aligned} R(W) = Tr(\textbf{W}^T \textbf{X}^T \textbf{LXW}) \end{aligned}$$
where [math]\displaystyle{ \mathbf{L} }[/math] is a Laplacian matrix that indicates the relationship between features.
This gives a final objective function of:
$$\begin{aligned} \mathop{min}_{\textbf{W}} \sum_{i=1}^n ||Xw_i - x_i||^2 + \rho_1||\textbf{W}|| + \rho_2R(\textbf{W}) \end{aligned}$$
Since this is a convex function, an iterative method can be used to optimize it to find the optimal solution [math]\displaystyle{ \mathbf{W^*} }[/math].
Calculate k for training set
Each element [math]\displaystyle{ w_{ij} }[/math] in [math]\displaystyle{ \textbf{W*} }[/math] represents the correlation between the ith and jth training sample so if a value is 0, it can be concluded that the jth training sample has no effect on the ith training sample which means that it should not be used in the prediction of the ith training sample. Consequently, all non-zero values in the [math]\displaystyle{ w_{.j} }[/math] vector would be useful in predicting the ith training sample which gives the result that the number of these non-zero elements for each sample is equal to the optimal k value for each sample.
For example, if there was a 4x4 training set where [math]\displaystyle{ \textbf{W*} }[/math] had the form:

The optimal k value for training sample 1 would be 2 since the correlation between training sample 1 and both training samples 2 and 4 is non-zero.
Train a Decision Tree using k as the label
k*Tree Classification
Experiments
In order to assess the performance of the proposed method against existing methods, a number of experiments were performed to measure classification accuracy and run time. The experiments were run on twenty public datasets provided by the UCI Repository of Machine Learning Data, and contained a mix of data types varying in size, in dimensionality, in the number of classes, and in imbalanced nature of the data. Ten-fold cross-validation was used to measure classification accuracy, and the following methods were compared against:
- k-Nearest Neighbor: The classical kNN approach with k set to k=1,5,10,20 and square root of the sample size [19]; the best result was reported.
- kNN-Based Applicability Domain Approach (AD-kNN) [33]
- kNN Method Based on Sparse Learning (S-kNN) [20]
- kNN Based on Graph Sparse Reconstruction (GS-kNN) [30]
- Filtered Attribute Subspace-based Bagging with Injected Randomness (FASBIR) [62], [63]
- Landmark-based Spectral Clustering kNN (LC-kNN) [64]
The experimental results were then assessed based on classification tasks that focused on different sample sizes, and tasks that focused on different numbers of features.
A. Experimental Results on Different Sample Sizes
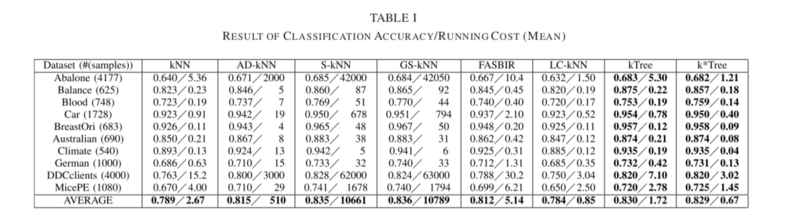
The running cost and (cross-validation) classification accuracy based on experiments on ten UCI datasets can be seen in Table I below.
The following key results are noted:
- Regarding classification accuracy, the proposed methods (kTree and k*Tree) outperformed kNN, AD-KNN, FASBIR, and LC-kNN on all datasets by 1.5%-4.5%, but had no notable improvements compared to GS-kNN and S-kNN.
- Classification methods which involved learning optimal k-values (for example the proposed kTree and k*Tree methods, or S-kNN, GS-kNN, AD-kNN) outperformed the methods with predefined k-values, such as traditional kNN.
- The proposed k*Tree method had the lowest running cost of all methods. However, the k*Tree method was still outperformed in terms of classification accuracy by GS-kNN and S-kNN, but ran on average 15 000 times faster than either method.
B. Experimental Results on Different Feature Numbers
The goal of this section was to evaluate the robustness of all methods under differing numbers of features; results can be seen in Table II below. The Fisher score [65] approach was used to rank and select the most information features in the datasets.
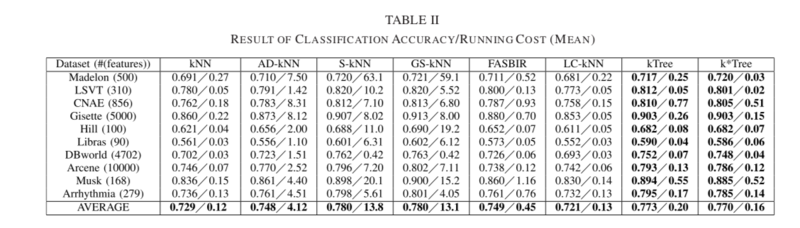
From Table II, the proposed kTree and k*Tree approaches outperformed kNN, AD-kNN, FASBIR and LC-KNN when tested for varying feature numbers. The S-kNN and GS-kNN approaches remained the best in terms of classification accuracy, but were greatly outperformed in terms of running cost by k*Tree. The cause for this is that k*Tree only scans a subsample of the training samples for kNN classification, while S-kNN and GS-kNN scan all training samples.
Conclusion
This paper introduced two novel approaches for kNN classification algorithms that can determine optimal k-values for each test sample. The proposed kTree and k*Tree methods achieve efficient classification by designing a training step that reduces the run time of the test stage. Based on the experimental results for varying sample sizes and differing feature numbers, it was observed that the proposed methods outperformed existing ones in terms of running cost while still achieving similar or better classification accuracies. Future areas of investigation could focus on the improvement of kTree and k*Tree for data with large numbers of features.
Critiques
- The paper only assessed classification accuracy through cross-validation accuracy. However, it would be interesting to investigate how the proposed methods perform using different metrics, such as AUC, precision-recall curves, or in terms of holdout test data set accuracy.
- The authors addressed that some of the UCI datasets contained imbalance data (such as the Climate and German data sets) while others did not. However, the nature of the class imbalance was not extreme, and the effect of imbalanced data on algorithm performance was not discussed or assessed. Moreover, it would have been interesting to see how the proposed algorithms performed on highly imbalanced datasets in conjunction with common techniques to address imbalance (e.g. oversampling, undersampling, etc.).
- While the authors contrast their ktTee and k*Tree approach with different kNN methods, the paper could contrast their results with more of the approaches discussed in the Related Work section of their paper. For example, it would be interesting to see how the kTree and k*Tree results compared to Góra and Wojna varied optimal k method.
References
[1] C. Zhang, Y. Qin, X. Zhu, and J. Zhang, “Clustering-based missing value imputation for data preprocessing,” in Proc. IEEE Int. Conf., Aug. 2006, pp. 1081–1086.
[2] Y. Song, J. Huang, D. Zhou, H. Zha, and C. L. Giles, “IKNN: Informative K-nearest neighbor pattern classification,” in Knowledge Discovery in Databases. Berlin, Germany: Springer, 2007, pp. 248–264.
[3] P. Vincent and Y. Bengio, “K-local hyperplane and convex distance nearest neighbor algorithms,” in Proc. NIPS, 2001, pp. 985–992.
[4] V. Premachandran and R. Kakarala, “Consensus of k-NNs for robust neighborhood selection on graph-based manifolds,” in Proc. CVPR, Jun. 2013, pp. 1594–1601.
[5] X. Zhu, S. Zhang, Z. Jin, Z. Zhang, and Z. Xu, “Missing value estimation for mixed-attribute data sets,” IEEE Trans. Knowl. Data Eng., vol. 23, no. 1, pp. 110–121, Jan. 2011.
[6] F. Sahigara, D. Ballabio, R. Todeschini, and V. Consonni, “Assessing the validity of QSARS for ready biodegradability of chemicals: An applicability domain perspective,” Current Comput.-Aided Drug Design, vol. 10, no. 2, pp. 137–147, 2013.
[7] S. Zhang, M. Zong, K. Sun, Y. Liu, and D. Cheng, “Efficient kNN algorithm based on graph sparse reconstruction,” in Proc. ADMA, 2014, pp. 356–369.
[8] X. Zhu, L. Zhang, and Z. Huang, “A sparse embedding and least variance encoding approach to hashing,” IEEE Trans. Image Process., vol. 23, no. 9, pp. 3737–3750, Sep. 2014.
[19] U. Lall and A. Sharma, “A nearest neighbor bootstrap for resampling hydrologic time series,” Water Resour. Res., vol. 32, no. 3, pp. 679–693, 1996.
[20] D. Cheng, S. Zhang, Z. Deng, Y. Zhu, and M. Zong, “KNN algorithm with data-driven k value,” in Proc. ADMA, 2014, pp. 499–512.
[30] S. Zhang, M. Zong, K. Sun, Y. Liu, and D. Cheng, “Efficient kNN algorithm based on graph sparse reconstruction,” in Proc. ADMA, 2014, pp. 356–369.
[33] F. Sahigara, D. Ballabio, R. Todeschini, and V. Consonni, “Assessing the validity of QSARS for ready biodegradability of chemicals: An applicability domain perspective,” Current Comput.-Aided Drug Design, vol. 10, no. 2, pp. 137–147, 2013.
[62] Z. H. Zhou and Y. Yu, “Ensembling local learners throughmultimodal perturbation,” IEEE Trans. Syst. Man, B, vol. 35, no. 4, pp. 725–735, Apr. 2005.
[63] Z. H. Zhou, Ensemble Methods: Foundations and Algorithms. London, U.K.: Chapman & Hall, 2012.
[64] Z. Deng, X. Zhu, D. Cheng, M. Zong, and S. Zhang, “Efficient kNN classification algorithm for big data,” Neurocomputing, vol. 195, pp. 143–148, Jun. 2016.
[65] K. Tsuda, M. Kawanabe, and K.-R. Müller, “Clustering with the fisher score,” in Proc. NIPS, 2002, pp. 729–736.