Dynamic Routing Between Capsules STAT946: Difference between revisions
(→Result) |
|||
| Line 44: | Line 44: | ||
= Dynamic Routing = | = Dynamic Routing = | ||
In the second section of this paper, authors give a mathematical representations for two key features in routing algorithm in capsule network, which are squashing and agreement. The general setting for this algorithm is between two arbitrary capsules i and j. Capsule j is assumed to be an arbitrary capsule from the first layer of capsules, and capsule i is an arbitrary capsule from the layer below. The purpose of routing algorithm is generate a vector output for routing decision between capsule j and capsule i. Furthermore, this vector output will be used in the decision for choice of dynamic routing. | In the second section of this paper, authors give a mathematical representations for two key features in routing algorithm in capsule network, which are squashing and agreement. The general setting for this algorithm is between two arbitrary capsules i and j. Capsule j is assumed to be an arbitrary capsule from the first layer of capsules, and capsule i is an arbitrary capsule from the layer below. The purpose of routing algorithm is to generate a vector output for routing decision between capsule j and capsule i. Furthermore, this vector output will be used in the decision for choice of dynamic routing. | ||
== Routing Algorithm == | == Routing Algorithm == | ||
Revision as of 10:50, 5 April 2018
Presented by
Yang, Tong(Richard)
Contributions
This paper introduces the concept of "capsules" and an approach to implement this concept in neural networks. Capsules are groups of neurons used to represent various properties of an entity/object present in the image, such as pose, deformation, and even the existence of the entity. Instead of the obvious representation of a logistic unit for the probability of existence, the paper explores using the length of the capsule output vector to represent existence, and the orientation to represent other properties of the entity. The paper makes the following major contributions:
- Proposes an alternative to max-pooling called routing-by-agreement.
- Demonstrates a mathematical structure for capsule layers and a routing mechanism. Builds a prototype architecture for capsule networks.
- Presented promising results that confirm the value of Capsnet as a new direction for development in deep learning.
Hinton's Critiques on CNN
In a past talk, Hinton tried to explain why max-pooling is the biggest problem with current convolutional networks. Here are some highlights from his talk.
Four arguments against pooling
- It is a bad fit to the psychology of shape perception: It does not explain why we assign intrinsic coordinate frames to objects and why they have such huge effects.
- It solves the wrong problem: We want equivariance, not invariance. Disentangling rather than discarding.
- It fails to use the underlying linear structure: It does not make use of the natural linear manifold that perfectly handles the largest source of variance in images.
- Pooling is a poor way to do dynamic routing: We need to route each part of the input to the neurons that know how to deal with it. Finding the best routing is equivalent to parsing the image.
Intuition Behind Capsules
We try to achieve viewpoint invariance in the activities of neurons by doing max-pooling. Invariance here means that by changing the input a little, the output still stays the same while the activity is just the output signal of a neuron. In other words, when in the input image we shift the object that we want to detect by a little bit, networks activities (outputs of neurons) will not change because of max pooling and the network will still detect the object. But the spacial relationships are not taken care of in this approach so instead capsules are used, because they encapsulate all important information about the state of the features they are detecting in a form of a vector. Capsules encode probability of detection of a feature as the length of their output vector. And the state of the detected feature is encoded as the direction in which that vector points to. So when detected feature moves around the image or its state somehow changes, the probability still stays the same (length of vector does not change), but its orientation changes.
Equivariance
To deal with the invariance problem of CNN, Hinton proposes the concept called equivariance, which is the foundation of capsule concept.
Two types of equivariance
Place-coded equivariance
If a low-level part moves to a very different position it will be represented by a different capsule.
Rate-coded equivariance
If a part only moves a small distance it will be represented by the same capsule but the pose outputs of the capsule will change.
Higher-level capsules have bigger domains so low-level place-coded equivariance gets converted into high-level rate-coded equivariance.
Dynamic Routing
In the second section of this paper, authors give a mathematical representations for two key features in routing algorithm in capsule network, which are squashing and agreement. The general setting for this algorithm is between two arbitrary capsules i and j. Capsule j is assumed to be an arbitrary capsule from the first layer of capsules, and capsule i is an arbitrary capsule from the layer below. The purpose of routing algorithm is to generate a vector output for routing decision between capsule j and capsule i. Furthermore, this vector output will be used in the decision for choice of dynamic routing.
Routing Algorithm
The routing algorithm is as the following:

In the following sections, each part of this algorithm will be explained in details.
Log Prior Probability
[math]\displaystyle{ b_{ij} }[/math] represents the log prior probabilities that capsule i should be coupled to capsule j, and updated in each routing iteration. As line 2 suggests, the initial values of [math]\displaystyle{ b_{ij} }[/math] for all possible pairs of capsules are set to 0. In the very first routing iteration, [math]\displaystyle{ b_{ij} }[/math] equals to zero. For each routing iteration, [math]\displaystyle{ b_{ij} }[/math] gets updated by the value of agreement, which will be explained later.
Coupling Coefficient
[math]\displaystyle{ c_{ij} }[/math] represents the coupling coefficient between capsule j and capsule i. It is calculated by applying the softmax function on the log prior probability [math]\displaystyle{ b_{ij} }[/math]. The mathematical transformation is shown below (Equation 3 in paper):
\begin{align} c_{ij} = \frac{exp(b_ij)}{\sum_{k}exp(b_ik)} \end{align}
[math]\displaystyle{ c_{ij} }[/math] are served as weights for computing the weighted sum and probabilities. Therefore, as probabilities, they have the following properties:
\begin{align} c_{ij} \geq 0, \forall i, j \end{align}
and,
\begin{align} \sum_{i,j}c_{ij} = 1, \forall i, j \end{align}
Predicted Output from Layer Below
[math]\displaystyle{ u_{i} }[/math] are the output vector from capsule i in the lower layer, and [math]\displaystyle{ \hat{u}_{j|i} }[/math] are the input vector for capsule j, which are the "prediction vectors" from the capsules in the layer below. [math]\displaystyle{ \hat{u}_{j|i} }[/math] is produced by multiplying [math]\displaystyle{ u_{i} }[/math] by a weight matrix [math]\displaystyle{ W_{ij} }[/math], such as the following:
\begin{align} \hat{u}_{j|i} = W_{ij}u_i \end{align}
where [math]\displaystyle{ W_{ij} }[/math] encodes some spatial relationship between capsule j and capsule i.
Capsule
By using the definitions from previous sections, the total input vector for an arbitrary capsule j can be defined as:
\begin{align} s_j = \sum_{i}c_{ij}\hat{u}_{j|i} \end{align}
which is a weighted sum over all prediction vectors by using coupling coefficients.
Squashing
The length of [math]\displaystyle{ s_j }[/math] is arbitrary, which is needed to be addressed with. The next step is to convert its length between 0 and 1, since we want the length of the output vector of a capsule to represent the probability that the entity represented by the capsule is present in the current input. The "squashing" process is shown below:
\begin{align} v_j = \frac{||s_j||^2}{1+||s_j||^2}\frac{s_j}{||s_j||} \end{align}
Notice that "squashing" is not just normalizing the vector into unit length. In addition, it does extra non-linear transformation to ensure that short vectors get shrunk to almost zero length and long vectors get shrunk to a length slightly below 1. The reason for doing this is to make decision of routing, which is called "routing by agreement" much easier to make between capsule layers.
Agreement
The final step of a routing iteration is to form an routing agreement [math]\displaystyle{ a_{ij} }[/math], which is represents as a scalar product:
\begin{align} a_{ij} = v_{j} \cdot \hat{u}_{j|i} \end{align}
As we mentioned in "squashing" section, the length of [math]\displaystyle{ v_{j} }[/math] is either close to 0 or close to 1, which will effect the magnitude of [math]\displaystyle{ a_{ij} }[/math] in this case. Therefore, the magnitude of [math]\displaystyle{ a_{ij} }[/math] indicate the how strong the routing algorithm agrees on taking the route between capsule j and capsule i. For each routing iteration, the log prior probability, [math]\displaystyle{ b_{ij} }[/math] will be updated by adding the value of its agreement value, which will effect how the coupling coefficients are computed in the next routing iteration. Because of the "squashing" process, we will eventually end up with a capsule j with its [math]\displaystyle{ v_{j} }[/math] close to 1 while all other capsules with its [math]\displaystyle{ v_{j} }[/math] close to 0, which indicates that this capsule j should be activated.
CapsNet Architecture
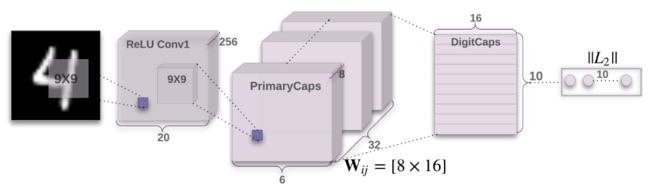
The second part of this paper discuss the experiment results from a 3-layer CapsNet, the architecture can be divided into two parts, encoder and decoder.
Encoder
How many routing iteration to use?
In appendix A of this paper, the authors have shown the empirical results from 500 epochs of training at different choice of routing iterations. According to their observation, more routing iterations increases the capacity of CapsNet but tends to bring additional risk of overfitting. Moreover, CapsNet with routing iterations less than three are not effective in general. As result, they suggest 3 iterations of routing for all experiments.
Marginal loss for digit existence
The experiments performed include segmenting overlapping digits on MultiMINST data set, so the loss function has be adjusted for presents of multiple digits. The marginal lose [math]\displaystyle{ L_k }[/math] for each capsule k is calculate by:
\begin{align} L_k = T_k max(0, m^+ - ||v_k||)^2 + \lambda(1 - T_k) max(0, ||v_k|| - m^-)^2 \end{align}
where [math]\displaystyle{ m^+ = 0.9 }[/math], [math]\displaystyle{ m^- = 0.1 }[/math], and [math]\displaystyle{ \lambda = 0.5 }[/math].
[math]\displaystyle{ T_k }[/math] is an indicator for presence of digit of class k, it takes value of 1 if and only if class k is presented. If class k is not presented, [math]\displaystyle{ \lambda }[/math] down-weight the loss which shrinks the lengths of the activity vectors for all the digit capsules. By doing this, The loss function penalizes the initial learning for all absent digit class, since we would like the top-level capsule for digit class k to have long instantiation vector if and only if that digit class is present in the input.
Layer 1: Conv1
The first layer of CapsNet. Similar to CNN, this is just convolutional layer that converts pixel intensities to activities of local feature detectors.
- Layer Type: Convolutional Layer.
- Input: [math]\displaystyle{ 28 \times 28 }[/math] pixels.
- Kernel size: [math]\displaystyle{ 9 \times 9 }[/math].
- Number of Kernels: 256.
- Activation function: ReLU.
- Output: [math]\displaystyle{ 20 \times 20 \times 256 }[/math] tensor.
Layer 2: PrimaryCapsules
The second layer is formed by 32 primary 8D capsules. By 8D, it means that each primary capsule contains 8 convolutional units with a [math]\displaystyle{ 9 \times 9 }[/math] kernel and a stride of 2. Each capsule will take a [math]\displaystyle{ 20 \times 20 \times 256 }[/math] tensor from Conv1 and produce an output of a [math]\displaystyle{ 6 \times 6 \times 8 }[/math] tensor.
- Layer Type: Convolutional Layer
- Input: [math]\displaystyle{ 20 \times 20 \times 256 }[/math] tensor.
- Number of capsules: 32.
- Number of convolutional units in each capsule: 8.
- Size of each convolutional unit: [math]\displaystyle{ 6 \times 6 }[/math].
- Output: [math]\displaystyle{ 6 \times 6 \times 8 }[/math] 8-dimensional vectors.
Layer 3: DigitsCaps
The last layer has 10 16D capsules, one for each digit. Not like the PrimaryCapsules layer, this layer is fully connected. Since this is the top capsule layer, dynamic routing mechanism will be applied between DigitsCaps and PrimaryCapsules. The process begins by taking a transformation of predicted output from PrimaryCapsules layer. Each output is a 8-dimensional vector, which needed to be mapped to a 16-dimensional space. Therefore, the weight matrix, [math]\displaystyle{ W_{ij} }[/math] is a [math]\displaystyle{ 8 \times 16 }[/math] matrix. The next step is to acquire coupling coefficients from routing algorithm and to perform "squashing" to get the output.
- Layer Type: Fully connected layer.
- Input: [math]\displaystyle{ 6 \times 6 \times 8 }[/math] 8-dimensional vectors.
- Output: [math]\displaystyle{ 16 \times 10 }[/math] matrix.
The loss function
The output of the loss function would be a ten-dimensional one-hot encoded vector with 9 zeros and 1 one at the correct position.
Regularization Method: Reconstruction
This is regularization method introduced in the implementation of CapsNet. The method is to introduce a reconstruction loss (scaled down by 0.0005) to margin loss during training. The authors argue this would encourage the digit capsules to encode the instantiation parameters the input digits. All the reconstruction during training is by using the true labels of the image input. The results from experiments also confirms that adding the reconstruction regularizer enforces the pose encoding in CapsNet and thus boots the performance of routing procedure.
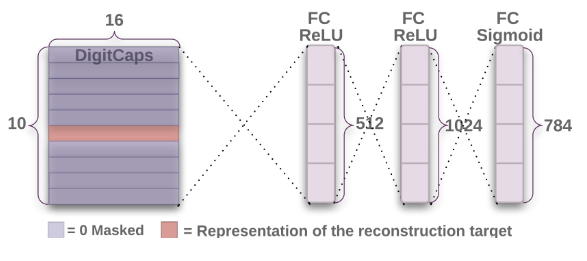
Decoder
The decoder consists of 3 fully connected layers, each layer maps pixel intensities to pixel intensities. The number of parameters in each layer and the activation functions used are indicated in the figure below:
Result
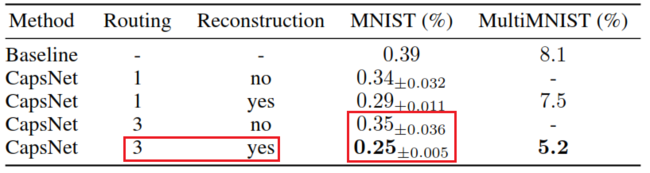
The authors include some results for CapsNet classification test accuracy to justify the result of reconstruction. We can see that for CapsNet with 1 routing iteration and CapsNet with 3 routing iterations, implement reconstruction shows significant improvements in both MINIST and MultiMINST data set. These improvements show the importance of routing and reconstruction regularizer.
Experiment Results for CapsNet
In this part, the authors demonstrate experiment results of CapsNet on different data sets, such as MINIST and different variation of MINST, such as expanded MINST, affNIST, MultiMNIST. Moreover, they also briefly discuss the performance on some other popular data set such CIFAR 10.
MINST
Highlights
- CapsNet archives state-of-the-art performance on MINST with significantly fewer parameters (3-layer baseline CNN model has 35.4M parameters, compared to 8.2M for CapsNet with reconstruction network).
- CapsNet with shallow structure (3 layers) achieves performance that only achieves by deeper network before.
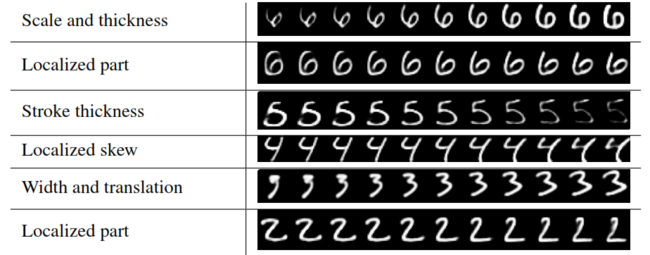
Interpretation of Each Capsule
The authors suggest that they found evidence that dimension of some capsule always captures some variance of the digit, while some others represents the global combinations of different variations, this would open some possibility for interpretation of capsules in the future. After computing the activity vector for the correct digit capsule, the authors fed perturbed versions of those activity vectors to the decoder to examine the effect on reconstruction. Some results from perturbations are shown below, where each row represents the reconstructions when one of the 16 dimensions in the DigitCaps representation is tweaked by intervals of 0.05 from the range [-0.25, 0.25]:
affNIST
affNIT data set contains different affine transformation of original MINST data set. By the concept of capsule, CapsNet should gain more robustness from its equivariance nature, and the result confirms this. Compare the baseline CNN, CapsNet achieves 13% improvement on accuracy.
MultiMNIST
The MultiMNIST is basically the overlapped version of MINIST. An important point to notice here is that this data set is generated by overlaying a digit on top of another digit from the same set but different class. In other words, the case of stacking digits from the same class is not allowed in MultiMINST. For example, stacking a 5 on a 0 is allowed, but stacking a 5 on another 5 is not. The reason is that CapsNet suffers from the "crowding" effect which will be discussed in the weakness of CapsNet section.
The architecture used for the training is same as the one used for MNIST dataset. However, decay step of the learning rate is 10x larger to account for the larger dataset. Even with the overlap in MultiMNIST, the network is able to segment both digits separately and it shows that the network is able to position and style of the object in the image.

Other data sets
CapsNet is used on other data sets such as CIFAR10, smallNORB and SVHN. The results are not comparable with state-of-the-art performance, but it is still promising since this architecture is the very first, while other networks have been development for a long time. The authors pointed out one drawback of CapsNet is that they tend to account for everything in the input images - in the CIFAR10 dataset, the image backgrounds were too varied to model in a reasonably sized network, which partly explains the poorer results.
Conclusion
This paper discuss the specific part of capsule network, which is the routing-by-agreement mechanism.
The authors suggest this is a great approach to solve the current problem with max-pooling in convolutional neural network. We see that the design of the capsule builds up upon the design of artificial neuron, but expands it to the vector form to allow for more powerful representational capabilities. It also introduces matrix weights to encode important hierarchical relationships between features of different layers. The result succeeds to achieve the goal of the designer: neuronal activity equivariance with respect to changes in inputs and invariance in probabilities of feature detection.
Moreover, as author mentioned, the approach mentioned in this paper is only one possible implementation of the capsule concept. Approaches like this have also been proposed to test other routing techniques.
The preliminary results from experiment using a simple shallow CapsNet also demonstrate unparalleled performance that indicates the capsules are a direction worth exploring.
Weakness of Capsule Network
- Routing algorithm introduces internal loops for each capsule. As number of capsules and layers increases, these internal loops may exponentially expand the training time.
- Capsule network suffers a perceptual phenomenon called "crowding", which is common for human vision as well. To address this weakness, capsules have to make a very strong representation assumption that at each location of the image, there is at most one instance of the type of entity that capsule represents. This is also the reason for not allowing overlaying digits from same class in generating process of MultiMINST.
- Other criticisms include that the design of capsule networks requires domain knowledge or feature engineering, contrary to the abstraction-oriented goals of deep learning.
Implementations
1) Tensorflow Implementation : https://github.com/naturomics/CapsNet-Tensorflow
2) Keras Implementation. : https://github.com/XifengGuo/CapsNet-Keras
References
- S. Sabour, N. Frosst, and G. E. Hinton, “Dynamic routing between capsules,” arXiv preprint arXiv:1710.09829v2, 2017
- “XifengGuo/CapsNet-Keras.” GitHub, 14 Dec. 2017, github.com/XifengGuo/CapsNet-Keras.
- “Naturomics/CapsNet-Tensorflow.” GitHub, 6 Mar. 2018, github.com/naturomics/CapsNet-Tensorflow.