Do Deep Neural Networks Suffer from Crowding
Still working on this.
Introduction
Ever since the evolution of Deep Networks, there has been tremendous amount of research and effort that has been put into making machines capable of recognizing objects the same way as humans do. Humans can recognize objects in a way that is invariant to scale, translation, and clutter. Crowding is another visual effect suffered by humans, in which an object that can be recognized in isolation can no longer be recognized when other objects, called flankers, are placed close to it and this is a very common real-life experience. This paper focuses on studying the impact of crowding on Deep Neural Networks (DNNs) by adding clutter to the images and then analyzing which models and settings suffer less from such effects.
The paper investigates two types of DNNs for crowding: traditional deep convolutional neural networks(DCNN) and a multi-scale eccentricity-dependent model which is an extension of the DCNNs and inspired by the retina where the receptive field size of the convolutional filters in the model grows with increasing distance from the center of the image, called the eccentricity and will be explained below. The authors focus on the dependence of crowding on image factors, such as flanker configuration, target-flanker similarity, target eccentricity and premature pooling in particular.
Models
Deep Convolutional Neural Networks
The DCNN is a basic architecture with 3 convolutional layers, spatial 3x3 max-pooling with varying strides and a fully connected layer for classification as shown in the below figure.
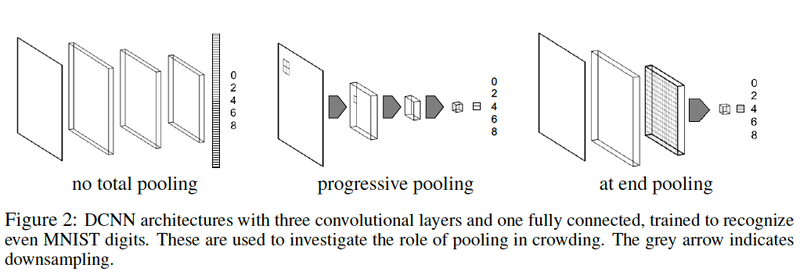
The network is fed with images resized to 60x60, with minibatches of 128 images, 32 feature channels for all convolutional layers, and convolutional filters of size 5x5 and stride 1.
As highlighted earlier, the effect of pooling is into main consideration and hence three different configurations have been investigated as below:
1. No total pooling Feature maps sizes decrease only due to boundary effects, as the 3x3 max pooling has stride 1. The square feature maps sizes after each pool layer are 60-54-48-42.
2. Progressive pooling 3x3 pooling with a stride of 2 halves the square size of the feature maps, until we pool over what remains in the final layer, getting rid of any spatial information before the fully connected layer. (60-27-11-1).
3. At end pooling Same as no total pooling, but before the fully connected layer, max-pool over the entire feature map. (60-54-48-1).
Eccentricity-dependent Model
The eccentricity-dependent model computes an invariant representation by sampling the inverted pyramid at a discrete set of scales with the same number of filters at each scale. At larger scales, the receptive fields of the filters are also larger to cover a larger image area, see Fig 3(a). Thus, the model constructs a multi-scale representation of the input, where smaller sections (crops) of the image are sampled densely at a high resolution, and larger sections (crops) are sampled with at a lower resolution, with each scale represented using the same number of pixels, as shown in Fig . Each scale is treated as an input channel to the network and then processed by convolutional filters, the weights of which are shared also across scales as well as space. Because of the downsampling of the input image, this is equivalent to having receptive fields of varying sizes. These shared parameters also allow the model to learn a scale invariant representation of the image.
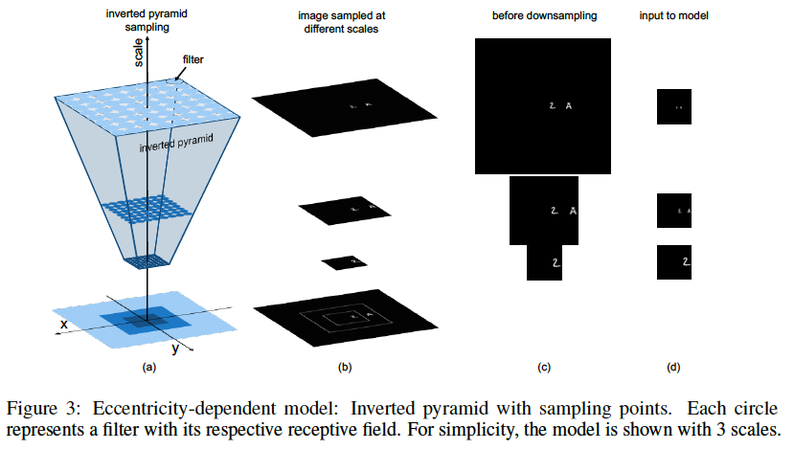
Scale pooling reduces the number of scales by taking the maximum value of corresponding locations in the feature maps across multiple scales. We set the spatial pooling constant using At end pooling, as described above. The type of scale pooling is indicated by writing the number of scales remaining in each layer, e.g. 11-1-1-1-1. The three configurations tested for scale pooling are (1) at the beginning, in which all the different scales are pooled together after the first layer, 11-1-1-1-1 (2) progressively, 11-7-5-3-1 and (3) at the end, 11-11-11-11-1, in which all 11 scales are pooled together at the last layer.
Contrast Normalization
Since we have multiple scales of input image, we perform normalization such that the sum of the pixel intensities in each scale is in the same range [0,1] followed by dividing them by a factor proportional to the crop area.