Dense Passage Retrieval for Open-Domain Question Answering: Difference between revisions
No edit summary |
|||
| Line 94: | Line 94: | ||
Here <math> \textbf{P}_i \in \mathbb{R}^{L \times h}</math> used in (1) and (2), <math>i</math> is one of the <math> k </math> passages and <math> h </math> is the hidden layer dimension of BERT's output. Additionally, <math> \hat{\textbf{P}} = [\textbf{P}^{[CLS]}_1,...,\textbf{P}^{[CLS]}_k] \in \mathbb{R}^{h \times k}</math>. Here <math> \textbf{w}_{start},\textbf{w}_{end},\textbf{w}_{selected} </math> are learnable vectors. The span score for <math> s </math>-th starting word to the <math> t</math>-th ending word of the <math> i </math>-th passage then can be calculated as <math> P_{start,i}(s) \times P_{end,i}(t) </math> where <math> s,t </math> are used to select the corresponding index of <math> \textbf{P}_{start,i}, \textbf{P}_{end,i} </math> respectively. The passage selection score for the <math> i</math>-th passage can be computed similarly, by indexing the <math>i</math>-th element of <math>\textbf{P}_{selected}</math>. | Here <math> \textbf{P}_i \in \mathbb{R}^{L \times h}</math> used in (1) and (2), <math>i</math> is one of the <math> k </math> passages and <math> h </math> is the hidden layer dimension of BERT's output. Additionally, <math> \hat{\textbf{P}} = [\textbf{P}^{[CLS]}_1,...,\textbf{P}^{[CLS]}_k] \in \mathbb{R}^{h \times k}</math>. Here <math> \textbf{w}_{start},\textbf{w}_{end},\textbf{w}_{selected} </math> are learnable vectors. The span score for <math> s </math>-th starting word to the <math> t</math>-th ending word of the <math> i </math>-th passage then can be calculated as <math> P_{start,i}(s) \times P_{end,i}(t) </math> where <math> s,t </math> are used to select the corresponding index of <math> \textbf{P}_{start,i}, \textbf{P}_{end,i} </math> respectively. The passage selection score for the <math> i</math>-th passage can be computed similarly, by indexing the <math>i</math>-th element of <math>\textbf{P}_{selected}</math>. | ||
== Source Code == | == Source Code == | ||
The code for this paper is freely available at https://github.com/facebookresearch/DPR. | |||
= Conclusion = | = Conclusion = | ||
In conclusion, this paper proposed a dense retrieval method which can generally outperform traditional bag-of-words methods in open domain question answering tasks. Dense retrieval methods make use of pre-training language model Bert and achieved state-of-art performance on many QA datasets. Dense retrieval methods are good at capturing word variants and semantic relationships, but are relatively weak at capturing exact keyword match. This paper also covers a few training techniques that are required to successfully train a dense retriever. Overall, learning dense representations for first stage retrieval can potentially improve QA system performance, and has received more attention. | In conclusion, this paper proposed a dense retrieval method which can generally outperform traditional bag-of-words methods in open domain question answering tasks. Dense retrieval methods make use of pre-training language model Bert and achieved state-of-art performance on many QA datasets. Dense retrieval methods are good at capturing word variants and semantic relationships, but are relatively weak at capturing exact keyword match. This paper also covers a few training techniques that are required to successfully train a dense retriever. Overall, learning dense representations for first stage retrieval can potentially improve QA system performance, and has received more attention. | ||
Revision as of 00:48, 29 November 2020
Presented by
Nicole Yan
Introduction
Open domain question answering is a task that finds question answers from a large collection of documents. Nowadays open domain QA systems usually use a two-stage framework: (1) a retriever that selects a subset of documents, and (2) a reader that fully reads the document subset and selects the answer spans. Stage one (1) is usually done through bag-of-words models, which count overlapping words and their frequencies in documents. Each document is represented by a high-dimensional, sparse vector. A common bag-of-words method that has been used for years is BM25, which ranks all documents based on the query terms appearing in each document. Stage one produces a small subset of documents where the answer might appear, and then in stage two, a reader would read the subset and locate the answer spans. Stage two is usually done through neural models, like Bert. While stage two benefits a lot from the recent advancement of neural language models, stage one still relies on traditional term-based models. This paper tries to improve stage one by using dense retrieval methods that generate dense, latent semantic document embedding, and demonstrates that dense retrieval methods can not only outperform BM25, but also improve the end-to-end QA accuracies.
Background
The following example clearly shows what problems open domain QA systems tackle. Given a question: "What is Uranus?", a system should find the answer spans from a large corpus. The corpus size can be billions of documents. In stage one, a retriever would select a small set of potentially relevant documents, which then would be fed to a neural reader in stage two for the answer spans extraction. Only a filtered subset of documents is processed by a neural reader since neural reading comprehension is expensive. It's impractical to process billions of documents using a neural reader.
Mathematical Formulation
Let's assume that we have a collection of [math]\displaystyle{ D }[/math] documents [math]\displaystyle{ d_1, d_2, \cdots, d_D }[/math] where each [math]\displaystyle{ d }[/math] is split into text passages of equal lengths as the basic retrieval units. Then the total number of passages is [math]\displaystyle{ M }[/math] in the corpus [math]\displaystyle{ \mathcal{C} = \{p_1, p_2, \ldots, p_{M}\} }[/math]. Each passage [math]\displaystyle{ p_i }[/math] is composed of a sequence of tokens [math]\displaystyle{ w^{(i)}_1, w^{(i)}_2, \cdots, w^{(i)}_{|p_i|} }[/math]. The task is to find a span of tokens [math]\displaystyle{ w^{(i)}_s, w^{(i)}_{s+1}, \cdots, w^{(i)}_{e} }[/math] from one of the passages [math]\displaystyle{ p_i }[/math] to answer the given question [math]\displaystyle{ q_i }[/math] . The corpus can contain millions of documents just to cover a wide variety of domains (e.g. Wikipedia) or even billions of them (e.g. the Web). The open-domain QA systems define the retriever as a function [math]\displaystyle{ R:(q,\mathcal{C}) \rightarrow \mathcal{C_F} }[/math] that takes as input a question [math]\displaystyle{ q }[/math] and a corpus [math]\displaystyle{ \mathcal{C} }[/math] and then returns a much smaller filter set of texts [math]\displaystyle{ \mathcal{C_F} \subset \mathcal{C} }[/math] , where [math]\displaystyle{ |\mathcal{C_F}| = k \ll |\mathcal{C}| }[/math]. The retriever can be evaluated by top-k retrieval accuracy that represents the fraction of relevant answers contained in [math]\displaystyle{ \mathcal{C_F} }[/math].
Dense Passage Retriever
This paper focuses on improving the retrieval component and proposed a framework called Dense Passage Retriever (DPR) which aims to efficiently retrieve the top K most relevant passages from a large passage collection. The key component of DPR is a dual-BERT model which encodes queries and passages in a vector space where relevant pairs of queries and passages are closer than irrelevant ones.
Model Architecture Overview
DPR has two independent BERT encoders: a query encoder Eq, and a passage encoder Ep. They map each input sentence to a d dimensional real-valued vector, and the similarity between a query and a passage is defined as the dot product of their vectors. DPR uses the [CLS] token output as embedding vectors, so d = 768. During the inference time, they used FAISS (Johnson et al., 2017) for the similarity search, which can be efficiently applied on billions of dense vectors
Training
The goal in training the encoders is to create a vector space where the relevant pairs of question and passages (positive passages) have smaller distance than the irrelevant ones (negative passages) which is a metric learning problem. The training data can be viewed as m instances of (query, positive passage, negative passages) pairs. The loss function is defined as the negative log likelihood of the positive passages. \begin{eqnarray} && L(q_i, p^+_i, p^-_{i,1}, \cdots, p^-_{i,n}) \label{eq:training} \\ &=& -\log \frac{ e^{\mathrm{sim}(q_i, p_i^+)} }{e^{\mathrm{sim}(q_i, p_i^+)} + \sum_{j=1}^n{e^{\mathrm{sim}(q_i, p^-_{i,j})}}}. \nonumber \end{eqnarray} While positive passage selection is simple, where the passage containing the answer is selected, negative passage selection is less explicit. The authors experimented with three types of negative passages: (1) Random passage from the corpus; (2) false positive passages returned by BM25; (3) Gold positive passages from the training set — i.e., a positive passage for one query is considered as a negative passage for another query. The authors got the best model by using gold positive passages from the same batch as negatives. This trick is called in-batch negatives. Assume there are B pairs of (query [math]\displaystyle{ q_i }[/math], positive passage [math]\displaystyle{ p_i }[/math]) in a mini-batch, then the negative passages for query [math]\displaystyle{ q_i }[/math] are the passages [math]\displaystyle{ p_i }[/math] when [math]\displaystyle{ j }[/math] is not equal to [math]\displaystyle{ i }[/math].
Experimental Setup
The authors pre-processed Wikipedia documents, i.e. they removed semi-structured data, such as tables, info- boxes, lists, as well as the disambiguation pages and then splitted each document into passages of length 100 words. These passages form a candidate pool. The five QA datasets described below were used to build the train data.
- Natural Questions (NQ) (Kwiatkowski et al., 2019): This was designed for the end-end question-answering tasks where the questions are Google search queries and the answers are annotated texts from the Wikipedia.
- TriviaQA (Joshi et al., 2017): It is a collection of trivia questions and answers scraped from the Web.
- WebQuestions (WQ) (Berant et al., 2013): It consists of questions selected using Google Search API where the answers are entities in Freebase
- CuratedTREC (TREC) (Baudisˇ and Sˇedivy`, 2015): It is intended for the open-domain QA from unstructured corpora. It consists of TREC QA tracks and questions from other Web sources.
- SQuAD v1.1 (Rajpurkar et al., 2016): It is a popular benchmark dataset for reading comprehension. The annotators were given a paragraph from the Wikipedia and were supposed to write questions which answers could be found in the given text.
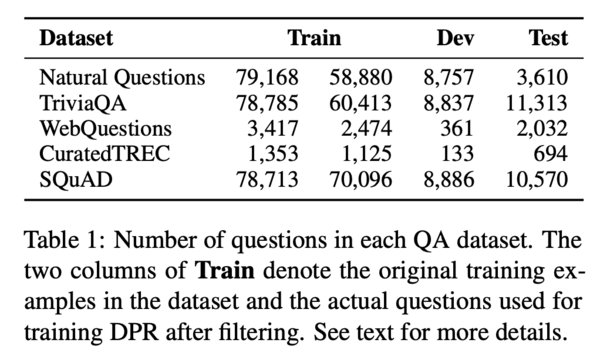
To build the training data, the authors match each question in the five datasets with a passage that contains the correct answer. The dataset statistics are summarized below.
Retrieval Performance Evaluation
The authors trained DPR on five datasets separately, and on the combined dataset. They compared DPR performance with the performance of the term-frequency based model BM25, and BM25+DPR. The DPR performance is evaluated in terms of the retrieval accuracy, ablation study, qualitative analysis, and run-time efficiency.
Main Results
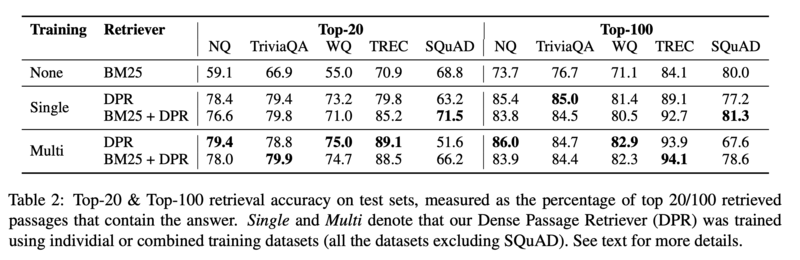
The table below compares the top-k (for k=20 or k=100) accuracies of different retrieval systems on various popular QA datasets. Top-k accuracy is the percentage of examples in the test set for which the correct outcome occurs in the k most likely outcomes as predicted by the network. As can be seen, DPR consistently outperforms BM25 on all datasets, with the exception of SQuAD. Additionally, DPR tends to perform particularly well when a smaller k value in chosen. The authors speculated that the lower performance of DPR on SQuAD was for two reasons inherent to the dataset itself. First, the SQuAD dataset has high lexical overlap between passages and questions. Second, the dataset is biased because it is collected from a small number of Wikipedia articles - a point which has been argued by other researchers as well.
Ablation Study on Model Training
The authors further analyzed how different training options would influence the model performance. The five training options they studied are (1) Sample efficiency, (2) In-batch negative training, (3) Impact of gold passages, (4) Similarity and loss, and (5) Cross-dataset generalization.
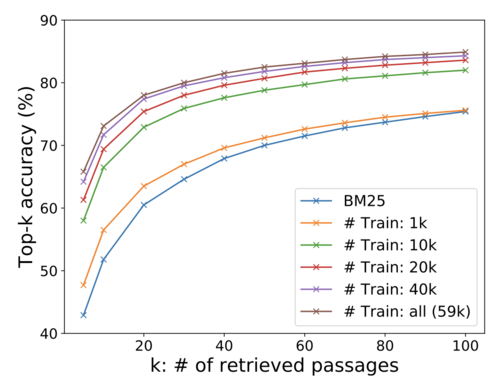
(1) Sample efficiency
The authors examined how many training examples were needed to achieve good performance. The study showed that DPR trained with 1k examples already outperformed BM25. With more training data, DPR performs better.
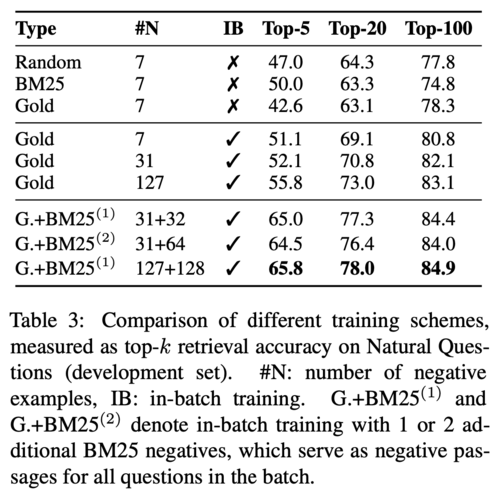
(2) In-batch negative training
Three training schemes are evaluated on the development dataset. The first scheme, which is the standard 1-to-N training setting, is to pair each query with one positive passage and n negative passages. As mentioned before, there are three ways to select negative passages: random, BM25, and gold. The results showed that in this setting, the choices of negative passages did not have strong impact on the model performance. The top block of the table below shows the retrieval accuracy in the 1-to-N setting. The second scheme, which is called in-batch negative setting, is to use positive passages for other queries in the same batch as negatives. The middle block shows the in-batch negative training results. The performance is significantly improved compared to the first setting. The last scheme is to augment in-batch negative with addition hard negative passages that are high ranked by BM25, but do not contain the correct answer. The bottom block shows the result for this setting, and the authors found that adding one addition BM25 hard negatives works the best.
(3) Similarity and loss In this paper, the similarity between a query and a passage is measured by the dot product of the two vectors, and the loss function is defined as the negative log likelihood of the positive passages. The authors experimented with other similarity functions such as L2-norm and cosine distance, and other loss functions such as triplet loss. The results showed these options didn't improve the model performance much.
(4) Cross-dataset generalization Cross-dataset generalization studies if a model trained on one dataset can perform well on other unseen datasets. The authors trained DPR on Natural Questions dataset and tested it on WebQuestions and CuratedTREC. The result showed DPR generalized well, with only 3~5 points loss.
Qualitative Analysis
Since BM25 is a bag-of-words method which ranks passages based on term-frequency, it's good at exact keywords and phrase matching, while DPR can capture lexical variants and semantic relationships. Generally DPR outperforms BM25 on the test sets.
Run-time Efficiency
The time required for generating dense embeddings and indexing passages is long. It took the authors 8.8 hours to encode 21-million passages on 8 GPUs, and 8.5 hours to index 21-million passages on a singe server. Conversely, building inverted index for 21-million passages only takes about 30 minutes. However, after the pre-processing is done, DPR can process 995 queries per second, while BM25 processes 23.7 queries per second.
Experiments: Question Answering
The authors evaluated DPR on end-to-end QA systems (i.e., retriever + neural reader). The results showed that higher retriever accuracy typically leads to better final QA results, and the passages retrieved by DPR are more likely to contain the correct answers. As shown in the table below, QA systems using DPR generally perform better, except for SQuAD.
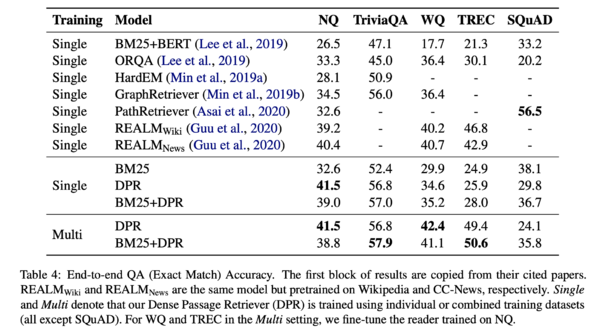
Reader for End-to-End
The reader used would score the subset of [math]\displaystyle{ k }[/math] passages which were retrieved using DPR. Next, the reader would extract an answer span from each passage and assign a span score. The best span from the passage with the highest selection score is chosen as the final answer. To calculate these scores linear layers followed by a softmax are applied on top of the BERT output as follows:
[math]\displaystyle{ \textbf{P}_{start,i}= softmax(\textbf{P}_i \textbf{w}_{start}) \in \mathbb{R}^L }[/math] where [math]\displaystyle{ L }[/math] is the number of words in the passage. (1)
[math]\displaystyle{ \textbf{P}_{end,i}= softmax(\textbf{P}_i \textbf{w}_{start}) \in \mathbb{R}^L }[/math] where [math]\displaystyle{ L }[/math] is the number of words in the passage. (2)
[math]\displaystyle{ \textbf{P}_{selected}= softmax(\hat{\textbf{P}}^T_i \textbf{w}_{selected}) \in \mathbb{R}^k }[/math] where [math]\displaystyle{ k }[/math] is the number of passages. (3)
Here [math]\displaystyle{ \textbf{P}_i \in \mathbb{R}^{L \times h} }[/math] used in (1) and (2), [math]\displaystyle{ i }[/math] is one of the [math]\displaystyle{ k }[/math] passages and [math]\displaystyle{ h }[/math] is the hidden layer dimension of BERT's output. Additionally, [math]\displaystyle{ \hat{\textbf{P}} = [\textbf{P}^{[CLS]}_1,...,\textbf{P}^{[CLS]}_k] \in \mathbb{R}^{h \times k} }[/math]. Here [math]\displaystyle{ \textbf{w}_{start},\textbf{w}_{end},\textbf{w}_{selected} }[/math] are learnable vectors. The span score for [math]\displaystyle{ s }[/math]-th starting word to the [math]\displaystyle{ t }[/math]-th ending word of the [math]\displaystyle{ i }[/math]-th passage then can be calculated as [math]\displaystyle{ P_{start,i}(s) \times P_{end,i}(t) }[/math] where [math]\displaystyle{ s,t }[/math] are used to select the corresponding index of [math]\displaystyle{ \textbf{P}_{start,i}, \textbf{P}_{end,i} }[/math] respectively. The passage selection score for the [math]\displaystyle{ i }[/math]-th passage can be computed similarly, by indexing the [math]\displaystyle{ i }[/math]-th element of [math]\displaystyle{ \textbf{P}_{selected} }[/math].
Source Code
The code for this paper is freely available at https://github.com/facebookresearch/DPR.
Conclusion
In conclusion, this paper proposed a dense retrieval method which can generally outperform traditional bag-of-words methods in open domain question answering tasks. Dense retrieval methods make use of pre-training language model Bert and achieved state-of-art performance on many QA datasets. Dense retrieval methods are good at capturing word variants and semantic relationships, but are relatively weak at capturing exact keyword match. This paper also covers a few training techniques that are required to successfully train a dense retriever. Overall, learning dense representations for first stage retrieval can potentially improve QA system performance, and has received more attention.
References
[1] Vladimir Karpukhin, Barlas Oğuz, Sewon Min, Patrick Lewis, Ledell Wu, Sergey Edunov, Danqi Chen, Wen-tau Yih. Dense Passage Retrieval for Open-Domain Question Answering. EMNLP 2020.