Deep Exploration via Bootstrapped DQN: Difference between revisions
Ashishgaurav (talk | contribs) No edit summary |
|||
| Line 64: | Line 64: | ||
# Samples from the NN trained on the original data do not look like a reasonable posterior (very spiky). | # Samples from the NN trained on the original data do not look like a reasonable posterior (very spiky). | ||
# The trained NN collapses to zero uncertainty at the data points from the original data. | # The trained NN collapses to zero uncertainty at the data points from the original data. | ||
== Deep Q Learning <sup>[[#References|[5]]]</sup> == | |||
At any point of time, our rewards dictate what our actions should be. Also, in general, we want good long term rewards. For example, if we are playing a first person shooter game, it is a good idea to go out of cover to kill an enemy, even if some health is lost. Similarly, in reinforcement learning, we want to maximize our long term reward. So if at each time $t$, the reward is $r_t$, then a naive way is to say we want to maximise | |||
$$ | |||
R_t = \sum_{i=0}^{\infty}r_t | |||
$$ | |||
But, this reward is unbounded. So technically it could tend to $\infty$ in a lot of the cases. This is why we use a '''discounted reward'''. | |||
$$ | |||
R_t = \sum_{i=0}^{\infty}\gamma^t r_t | |||
$$ | |||
Here, we take $0\leq \gamma \lt 1$. So, what this means is that we value our current reward the most ($r_0$ has a coefficient of $1$), but we also consider the future possible rewards. So if we had two choices: get $+4$ now and $0$ at all other timesteps, or get $-2$ now and $+2$ after $3$ timesteps for $20$ timesteps, we choose the latter ($\gamma=0.9$). This is because $(+4) < (-2)+0.9^3(2+0.9\cdot2+\cdots+0.9^{19}\cdot2)$. | |||
A '''policy''' $\pi: \mathbb{S} \rightarrow \mathbb{A}$ is just a function that tells us what action to take in a given state $s\in \mathbb{S}$. Our goal is to find the best policy $\pi^*$ that maximises the reward from a given state $s$. So, a '''value function''' is defined from $s$ (which the agent is in, at timestep $t$) and following the policy $\pi$ as $V^\pi(s) = \mathbb{E}[R_t]$. The optimal value function is then simply | |||
$$ | |||
V^*(s)=\displaystyle\max_{\pi}V^\pi(s) | |||
$$ | |||
For convenience however, it is better to work with the '''Q function''' $Q: \mathbb{S}\times\mathbb{A} \rightarrow \mathbb{R}$. $Q$ is defined similarly as $V$. It is the expected return after taking an action $a$ in the given state $s$. So, $Q^\pi(s,a)=\mathbb{E}[R_t|s,a]$. The optimal $Q$ function is | |||
$$ | |||
Q^*(s,a)=\displaystyle\max_{\pi}Q^\pi(s,a) | |||
$$ | |||
Suppose that we know $Q^*$. Then, if we know that we are supposed to start at $s$ and take an action $a$ right now, what is the best course of action from the next time step? We just choose the optimal action $a'$ at the next state $s'$ that we reach. The optimal action $a'$ at state $s'$ is simply the argument $a_x$ that maximises our $Q^*(s',\cdot)$. | |||
$$ | |||
a'=\displaystyle\arg\max_{a_x} Q^*(s',a_x) | |||
$$ | |||
So, our best expected reward from $s$ taking action $a$ is $\mathbb{E}[r_t+\gamma\mathbb{E}[R_{t+1}]]$. This is known as the '''Bellman equation''': | |||
$$ | |||
Q^*(s,a)=\mathbb{E}[r_t+\gamma \displaystyle\arg\max_{a_x} Q^*(s',a_x)] | |||
$$ | |||
In Q learning, we use a deep neural network with weights $\theta$ as a function approximator for $Q^*$. The '''naive way''' to do this is to design a deep neural net that takes as input the state $s$ and action $a$, and produces an approximation to $Q^*$. | |||
* Suppose our neural net weights are $\theta_i$ at iteration $i$. | |||
* We want to train our neural net on the case when we are at $s$, take action $a$, get reward $r$, and reach $s'$. | |||
* To find out what action is best from $s'$, i.e. $a'$, we have to simulate all actions from $s'$. We can do this after we complete this iteration, then run $s',a_x$ for all $a_x\in\mathbb{A}$. But, we don't know how to complete this iteration without knowing this $a'$. So, another way is to simulate all actions from $s'$ using last known set of weights $\theta_{i-1}$. We just simulate state $s'$, action $a_x$ for all $a_x\in\mathbb{A}$ from the previous state and get $Q^*(s',a_x;\theta_{i-1})$. | |||
* Now we can compute our loss function using the Bellman equation, and backpropagate. | |||
$$ | |||
\mbox{loss}=\mbox{target}-\mbox{prediction}=(r+\displaystyle\max_{a_x}Q^*(s',a_x;\theta_{i-1}))-Q^*(s,a;\theta_i) | |||
$$ | |||
The '''problem''' with this approach is that at every iteration $i$, we have to do $|\mathbb{A}|$ forward passes on the previous set of weights $\theta_{i-1}$ to find out the best action $a'$ at $s'$. This becomes infeasible quickly with more possible actions. | |||
Authors of [[#References|[5]]] therefore use another kind of architecture. This architecture takes as input the state $s$, and computes the values $Q^*(s,a_x)$ for $a_x\in\mathbb{A}$. So there are $|\mathbb{A}|$ outputs. This basically parallelizes the forward passes so that $r+\displaystyle\max_{a_x}Q^*(s',a_x;\theta_{i-1})$ can be done with just a single pass through the outputs. | |||
[[File:DQN_arch.png|thumb||||600px|Source: [https://leonardoaraujosantos.gitbooks.io/artificial-inteligence/content/image_folder_7/DQNBreakoutBlocks.png leonardoaraujosantos.gitbooks.io]]] | |||
'''Note:''' When I say state $s$ as an input, I mean some representation of $s$. Since the environment is a partially observable MDP, it is hard to know $s$. So, we can for example, apply a convnet on the frames and get an idea of what the current state is. We pass this output to the input of the DNN (DNN is the fully connected layer for the convnet then). | |||
=== Experience Replay === | |||
Authors of this paper borrow the concept of experience replay from [[#References|[5,6]]]. In experience replay, we do training in episodes. In each episode, we play and store consecutive $(s,a,r,s')$ tuples in the experience replay buffer. Then after the play, we choose random samples from this buffer and do our training. | |||
Advantages of experience replay over simple online Q learning<sup>[[#References|[5]]]</sup>: | |||
* '''Better data efficiency''': It is better to use one transition many times to learn again and again, rather than just learn once from it. | |||
* Learning from consecutive samples is difficult because of correlated data. Experience replay breaks this correlation. | |||
* Online learning means the input is decided by the previous action. So, if the maximising action is to go left in some game, next inputs would be about what happens when we go left. This can cause the optimiser to get stuck in a feedback loop, or even diverge, as [[#Reference|[7]]] points out. | |||
== References == | == References == | ||
| Line 71: | Line 140: | ||
# [https://ocw.mit.edu/courses/mathematics/18-05-introduction-to-probability-and-statistics-spring-2014/readings/MIT18_05S14_Reading24.pdf Bootstrap confidence intervals, Class 24, 18.05, MIT Open Courseware] | # [https://ocw.mit.edu/courses/mathematics/18-05-introduction-to-probability-and-statistics-spring-2014/readings/MIT18_05S14_Reading24.pdf Bootstrap confidence intervals, Class 24, 18.05, MIT Open Courseware] | ||
# [https://arxiv.org/abs/1506.02142 Yarin Gal and Zoubin Ghahramani. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. arXiv preprint arXiv:1506.02142, 2015.] | # [https://arxiv.org/abs/1506.02142 Yarin Gal and Zoubin Ghahramani. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. arXiv preprint arXiv:1506.02142, 2015.] | ||
# [https://www.cs.toronto.edu/~vmnih/docs/dqn.pdf Mnih et al., Playing Atari with Deep Reinforcement Learning, 2015] | |||
# Long-Ji Lin. Reinforcement learning for robots using neural networks. Technical report, DTIC Document, 1993. | |||
# John N Tsitsiklis and Benjamin Van Roy. An analysis of temporal-difference learning with function approximation. Automatic Control, IEEE Transactions on, 42(5):674–690, 1997. | |||
Revision as of 22:56, 18 November 2017
Status: In Progress, please do not make a major edit!
Intro to Reinforcement Learning
In reinforcement learning, an agent interacts with an environment with the goal to maximize its long term reward. A common application of reinforcement learning is to the multi armed bandit problem. In a multi armed bandit problem, there is a gambler and there are $n$ slot machines, and the gambler can choose to play any specific slot machine at any time. All the slot machines have their own probability distributions by which they churn out rewards, but this is unknown to the gambler. So the question is, how can the gambler learn how to get the maximum long term reward?
There are two things the gambler can do at any instance: either he can try a new slot machine, or he can play the slot machine he has tried before (and he knows he will get some reward). However, even though trying a new slot machine feels like it would bring less reward to the gambler, it is possible that the gambler finds out a new slot machine that gives a better reward than the current best slot machine. This is the dilemma of exploration vs exploitation. Trying out a new slot machine is exploration, while redoing the best move so far is exploiting the currently understood perception of the reward.
There are many strategies to approach this exploration-exploitation dilemma. Some common strategies for optimizing in an exploration-exploitation setting are Random Walk, Curiosity-Driven Exploration, and Thompson Sampling. A lot of these approaches are provably efficient, but assume that the state space is not very large. For instance, the approach called Curiosity-Driven Exploration aims to take actions that lead to immediate additional information. This requires the model to search “every possible cell in the grid” which is not desirable if state space is very large. Strategies for large state spaces often just either ignore exploration, or do something naive like $\epsilon$-greedy, where you exploit with $1-\epsilon$ probability and explore "randomly" in rest of the cases.
This paper tries to use a Thompson sampling like approach to make decisions.
Thompson Sampling[1]
In Thompson sampling, our goal is to reach a belief that resembles the truth. Let's consider a case of coin tosses (2-armed bandit). Suppose we want to be able to reach a satisfactory pdf for $\mathbb{P}_h$ (heads). Assuming that this is a Bernoulli bandit problem, i.e. the rewards are $0$ or $1$, we can start off with $\mathbb{P}_h^{(0)}=\beta(1,1)$. The $\beta(x,y)$ distribution is a very good choice for a possible pdf because it works well for Bernoulli rewards. Further $\beta(1,1)$ is the uniform distribution $\mathbb{N}(0,1)$.
Now, at every iteration $t$, we observe the reward $R^{(t)}$ and try to make our belief close to the truth by doing a Bayesian computation. Assuming $p$ is the probability of getting a heads,
$$ \begin{align*} \mathbb{P}(R|D) &\propto \mathbb{P}(D|R) \cdot \mathbb{P}(R) \\ \mathbb{P}_h^{(t+1)}&\propto \mbox{likelihood}\cdot\mbox{prior} \\ &\propto p^{R^{(t)}}(1-p)^{R^{(t)}} \cdot \mathbb{P}_h^{(t)} \\ &\propto p^{R^{(t)}}(1-p)^{R^{(t)}} \cdot \beta(x_t, y_t) \\ &\propto p^{R^{(t)}}(1-p)^{R^{(t)}} \cdot p^{x_t-1}(1-p)^{y_t-1} \\ &\propto p^{x_t+R^{(t)}-1}(1-p)^{y_t+R^{(t)}-1} \\ &\propto \beta(x_t+R^{(t)}, y_t+R^{(t)}) \end{align*} $$
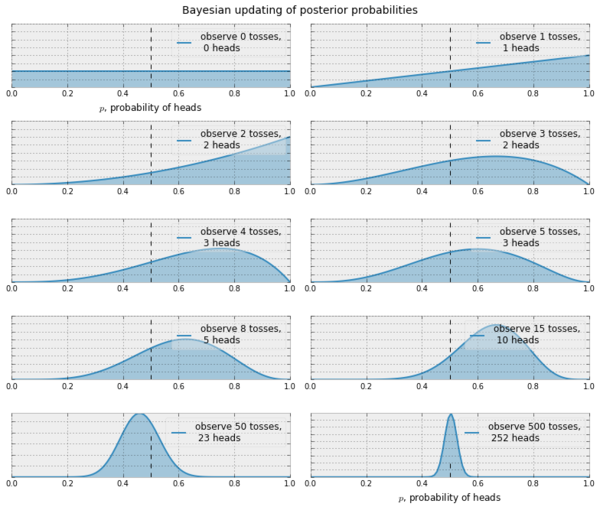
This means that with successive sampling, our belief can become better at approximating the truth. There are similar update rules if we use a non Bernoulli setting, say, Gaussian. In the Gaussian case, we start with $\mathbb{P}_h^{(0)}=\mathbb{N}(0,1)$ and given that $\mathbb{P}_h^{(t)}\propto\mathbb{N}(\mu, \sigma)$ it is possible to show that the update rule looks like
$$ \mathbb{P}_h^{(t+1)} \propto \mathbb{N}\bigg(\frac{t\mu+R^{(t)}}{t+1},\frac{\sigma}{\sigma+1}\bigg) $$
How can we use this in reinforcement learning?
We can use this idea to decide when to explore and when to exploit. We start with an initial belief, choose an action, observe the reward and based on the kind of reward, we update our belief about what action to choose next.
Bootstrapping [2,3]
This idea may be unfamiliar to some people, so I thought it would be a good idea to include this. In statistics, bootstrapping is a method to generate new samples from a given sample. Suppose that we have a given population, and we want to study a measure $\theta$. So, we just find $n$ sample points (sample $\{D_i\}_{i=1}^n$), calculate this measure $\hat{\theta}$ for these $n$ points, and make our inference.
If we later wish to find a better bound on $\hat{\theta}$, i.e. suppose we want to say that $\delta_1 \leq \hat{\theta} \leq \delta_2$ with a confidence of $c$, then we can use bootstrapping for this.
Using bootstrapping, we can create a new sample $\{D'_i\}_{i=1}^{n'}$ by randomly sampling $n'$ times from $D$, with replacement. So, if $D=\{1,2,3,4\}$, a $D'$ of size $n'=10$ could be $\{1,4,4,3,2,2,2,1,3,4\}$. We do this a sufficient $k$ number of times, calculate $\hat{\theta}$ each time, and thus get a distribution $\{\hat{\theta}_i\}_{i=1}^k$. Now, we can choose the $100\cdot c$th and $100\cdot(1-c)$th percentile of this distribution, (let them be $\hat{\theta}_\alpha$ and $\hat{\theta}_\beta$ respectively) and say
$$\hat{\theta}_\alpha \leq \hat{\theta} \leq \hat{\theta}_\beta, \mbox{with confidence }c$$
Why choose bootstrap and not dropout?
There is previous work[4] that establishes dropout as a good way to train NNs on a posterior such that the trained NN works like a function approximator that is close to the actual posterior. But, there are several problems with the predictions of this trained NN. The figures below are from the appendix of this paper. The left image is the NN trained by the authors of this paper on a sample noisy distribution and the right image is from the accompanying web demo from [4], where the authors of [4] show that their NN converges around the mean with a good confidence.
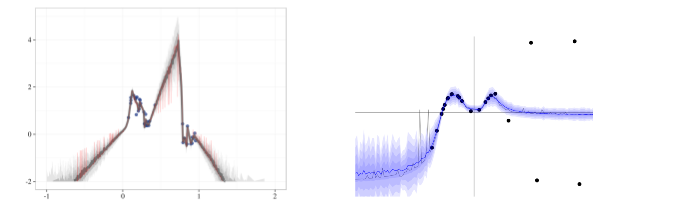
According to the authors of this paper,
- Even though [4] says that dropout converges arond the mean, their experiment actually behaves weirdly around a reasonable point like $x=0.75$. They think that this happens because dropout only affects the region local to the original data.
- Samples from the NN trained on the original data do not look like a reasonable posterior (very spiky).
- The trained NN collapses to zero uncertainty at the data points from the original data.
Deep Q Learning [5]
At any point of time, our rewards dictate what our actions should be. Also, in general, we want good long term rewards. For example, if we are playing a first person shooter game, it is a good idea to go out of cover to kill an enemy, even if some health is lost. Similarly, in reinforcement learning, we want to maximize our long term reward. So if at each time $t$, the reward is $r_t$, then a naive way is to say we want to maximise
$$ R_t = \sum_{i=0}^{\infty}r_t $$
But, this reward is unbounded. So technically it could tend to $\infty$ in a lot of the cases. This is why we use a discounted reward.
$$ R_t = \sum_{i=0}^{\infty}\gamma^t r_t $$
Here, we take $0\leq \gamma \lt 1$. So, what this means is that we value our current reward the most ($r_0$ has a coefficient of $1$), but we also consider the future possible rewards. So if we had two choices: get $+4$ now and $0$ at all other timesteps, or get $-2$ now and $+2$ after $3$ timesteps for $20$ timesteps, we choose the latter ($\gamma=0.9$). This is because $(+4) < (-2)+0.9^3(2+0.9\cdot2+\cdots+0.9^{19}\cdot2)$.
A policy $\pi: \mathbb{S} \rightarrow \mathbb{A}$ is just a function that tells us what action to take in a given state $s\in \mathbb{S}$. Our goal is to find the best policy $\pi^*$ that maximises the reward from a given state $s$. So, a value function is defined from $s$ (which the agent is in, at timestep $t$) and following the policy $\pi$ as $V^\pi(s) = \mathbb{E}[R_t]$. The optimal value function is then simply
$$ V^*(s)=\displaystyle\max_{\pi}V^\pi(s) $$
For convenience however, it is better to work with the Q function $Q: \mathbb{S}\times\mathbb{A} \rightarrow \mathbb{R}$. $Q$ is defined similarly as $V$. It is the expected return after taking an action $a$ in the given state $s$. So, $Q^\pi(s,a)=\mathbb{E}[R_t|s,a]$. The optimal $Q$ function is
$$ Q^*(s,a)=\displaystyle\max_{\pi}Q^\pi(s,a) $$
Suppose that we know $Q^*$. Then, if we know that we are supposed to start at $s$ and take an action $a$ right now, what is the best course of action from the next time step? We just choose the optimal action $a'$ at the next state $s'$ that we reach. The optimal action $a'$ at state $s'$ is simply the argument $a_x$ that maximises our $Q^*(s',\cdot)$.
$$ a'=\displaystyle\arg\max_{a_x} Q^*(s',a_x) $$
So, our best expected reward from $s$ taking action $a$ is $\mathbb{E}[r_t+\gamma\mathbb{E}[R_{t+1}]]$. This is known as the Bellman equation:
$$ Q^*(s,a)=\mathbb{E}[r_t+\gamma \displaystyle\arg\max_{a_x} Q^*(s',a_x)] $$
In Q learning, we use a deep neural network with weights $\theta$ as a function approximator for $Q^*$. The naive way to do this is to design a deep neural net that takes as input the state $s$ and action $a$, and produces an approximation to $Q^*$.
- Suppose our neural net weights are $\theta_i$ at iteration $i$.
- We want to train our neural net on the case when we are at $s$, take action $a$, get reward $r$, and reach $s'$.
- To find out what action is best from $s'$, i.e. $a'$, we have to simulate all actions from $s'$. We can do this after we complete this iteration, then run $s',a_x$ for all $a_x\in\mathbb{A}$. But, we don't know how to complete this iteration without knowing this $a'$. So, another way is to simulate all actions from $s'$ using last known set of weights $\theta_{i-1}$. We just simulate state $s'$, action $a_x$ for all $a_x\in\mathbb{A}$ from the previous state and get $Q^*(s',a_x;\theta_{i-1})$.
- Now we can compute our loss function using the Bellman equation, and backpropagate.
$$ \mbox{loss}=\mbox{target}-\mbox{prediction}=(r+\displaystyle\max_{a_x}Q^*(s',a_x;\theta_{i-1}))-Q^*(s,a;\theta_i) $$
The problem with this approach is that at every iteration $i$, we have to do $|\mathbb{A}|$ forward passes on the previous set of weights $\theta_{i-1}$ to find out the best action $a'$ at $s'$. This becomes infeasible quickly with more possible actions.
Authors of [5] therefore use another kind of architecture. This architecture takes as input the state $s$, and computes the values $Q^*(s,a_x)$ for $a_x\in\mathbb{A}$. So there are $|\mathbb{A}|$ outputs. This basically parallelizes the forward passes so that $r+\displaystyle\max_{a_x}Q^*(s',a_x;\theta_{i-1})$ can be done with just a single pass through the outputs.
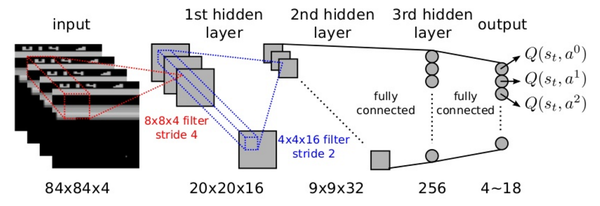
Note: When I say state $s$ as an input, I mean some representation of $s$. Since the environment is a partially observable MDP, it is hard to know $s$. So, we can for example, apply a convnet on the frames and get an idea of what the current state is. We pass this output to the input of the DNN (DNN is the fully connected layer for the convnet then).
Experience Replay
Authors of this paper borrow the concept of experience replay from [5,6]. In experience replay, we do training in episodes. In each episode, we play and store consecutive $(s,a,r,s')$ tuples in the experience replay buffer. Then after the play, we choose random samples from this buffer and do our training.
Advantages of experience replay over simple online Q learning[5]:
- Better data efficiency: It is better to use one transition many times to learn again and again, rather than just learn once from it.
- Learning from consecutive samples is difficult because of correlated data. Experience replay breaks this correlation.
- Online learning means the input is decided by the previous action. So, if the maximising action is to go left in some game, next inputs would be about what happens when we go left. This can cause the optimiser to get stuck in a feedback loop, or even diverge, as [7] points out.
References
- Learning and optimization for sequential decision making, Columbia University, Lec 4
- Thoughtco, What is bootstrapping in statistics?
- Bootstrap confidence intervals, Class 24, 18.05, MIT Open Courseware
- Yarin Gal and Zoubin Ghahramani. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. arXiv preprint arXiv:1506.02142, 2015.
- Mnih et al., Playing Atari with Deep Reinforcement Learning, 2015
- Long-Ji Lin. Reinforcement learning for robots using neural networks. Technical report, DTIC Document, 1993.
- John N Tsitsiklis and Benjamin Van Roy. An analysis of temporal-difference learning with function approximation. Automatic Control, IEEE Transactions on, 42(5):674–690, 1997.