Deep Double Descent Where Bigger Models and More Data Hurt
Presented By
Sam Senko, Tyler Verhaar and Ben Zhang
Models and Experiments
A variety of experiments were done to demonstrate the double descent phenomenon and its connection to effective model complexity in a number of different situations. Three main model architectures were used in these experiments:
- A simple convolutional neural network with 4 convolutional layers and 1 fully connected layer. The widths of the convolutional layers were k, 2k, 4k and 8k respectively where k is a parameter which was varied in the experiments.
- Resnets, introduced in (He, et al., 2016), with the convolutional layers having widths k, 2k, 4k and 8k respectively where k is again a parameter
- Transformers, a type of recurrent neural network often used in natural language processing. This used a 6-layer architecture. The embedding dimension was varied to vary the complexity of the model and the width of the fully connected layers was scaled proportionately to this embedding dimension.
The above models were trained with variants of gradient descent, with the number of gradient steps varying from around 5 thousand to around 500 thousand depending on the particular model and the experiment. In some experiments, label noise was used where, with probability p, the label was replaced by an incorrect label chosen uniformly at random.
The first experiment investigated the effect of varying model complexity at various levels of label noise. Results are given below:
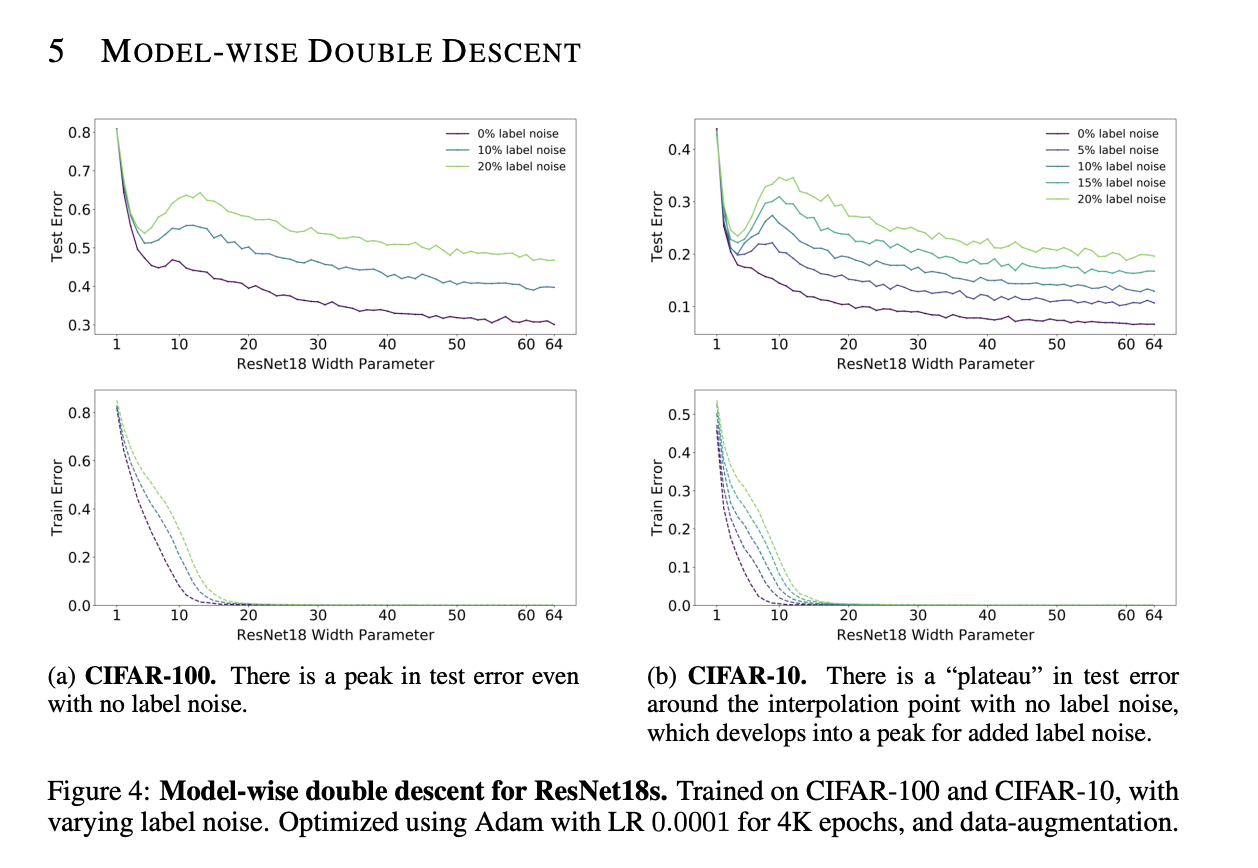 A few observations can be made, confirming the predictions of the paper authors. Firstly, there is double descent, with the test error decreasing until a certain point at which the model overfits leading to an increase in test error followed eventually by a second decrease in the test error. Additionally, at all levels of label noise, the peak occured around the threshold where the EMC is approximately the size of the dataset (and so the train error first approaches 0), confirming the hypotheses made by the authors. Finally, increasing label noise naturally moved this critical threshold further right which can be seen by the peaks being further right with more label noise.
A few observations can be made, confirming the predictions of the paper authors. Firstly, there is double descent, with the test error decreasing until a certain point at which the model overfits leading to an increase in test error followed eventually by a second decrease in the test error. Additionally, at all levels of label noise, the peak occured around the threshold where the EMC is approximately the size of the dataset (and so the train error first approaches 0), confirming the hypotheses made by the authors. Finally, increasing label noise naturally moved this critical threshold further right which can be seen by the peaks being further right with more label noise.
The next experiment investigated the effect of the number of epochs used on the test error for a variety of different model complexities. Note that increasing the number of epochs increases the EMC, although it may be impossible to reach a particular EMC without also increasing the model complexity.
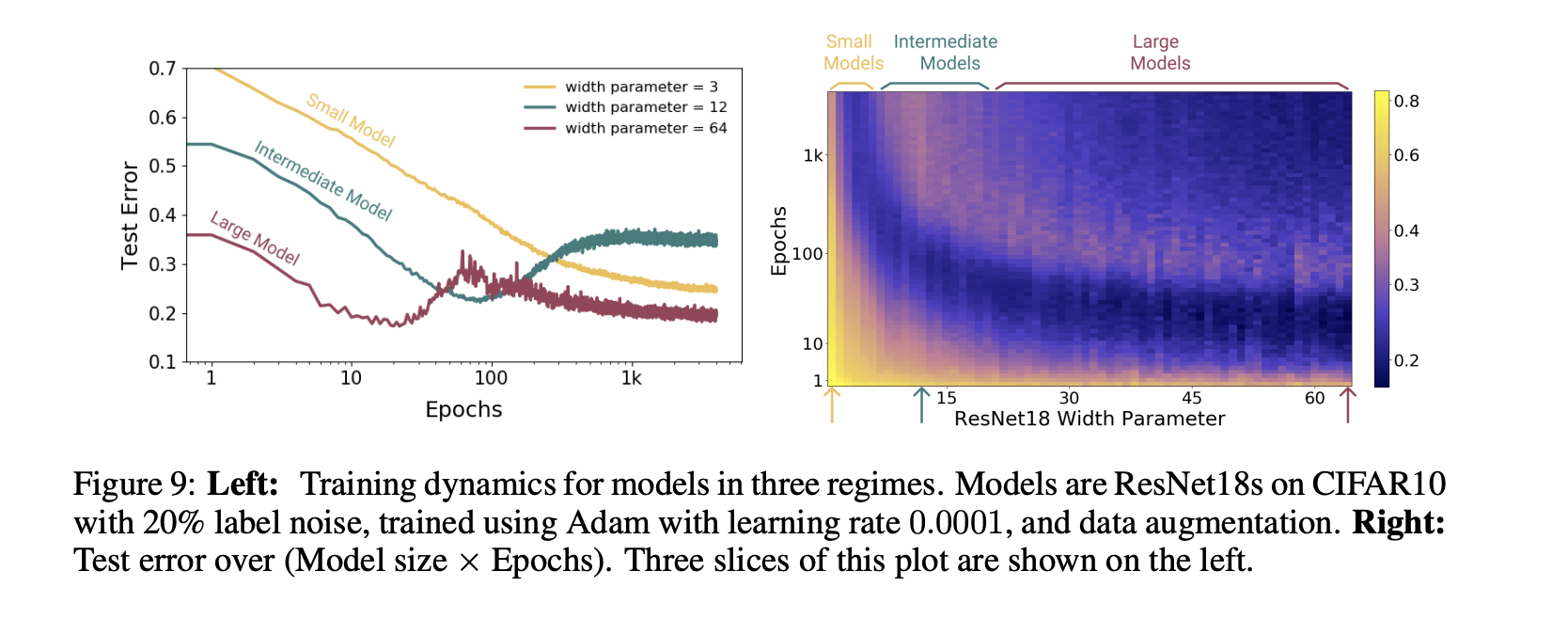 Here, we see that the small model is unable to reach a sufficiently large EMC to see overfitting begin. For the medium-sized model, the model is just barely able to reach an EMC of approximately the size of the data and, therefore, sees a traditional U-shaped curve without a further decrease in the test error. However, the large model, which is able to exceed the threshold where EMC is approximately the data size, does see a double descent as would be expected. This has the practical implication that certain forms of early stopping may not be effective for very large models, as they may stop before reaching the second descent.
Here, we see that the small model is unable to reach a sufficiently large EMC to see overfitting begin. For the medium-sized model, the model is just barely able to reach an EMC of approximately the size of the data and, therefore, sees a traditional U-shaped curve without a further decrease in the test error. However, the large model, which is able to exceed the threshold where EMC is approximately the data size, does see a double descent as would be expected. This has the practical implication that certain forms of early stopping may not be effective for very large models, as they may stop before reaching the second descent.